[Computer Vision] SIFT特征学习笔记

SIFT(Scale Invariant Feature Transform)，尺度空间不变特征，目前手工设计的最好vision特征。

以下是学习http://blog.csdn.net/zddblog/article/details/7521424后的收获。

一、尺度空间

gaussian pyramid的产生：

1、为避免对第一组第一层图片（原始图片）做高斯滤波导致损失，在其基础上将尺度扩大一倍作为-1层，方法是用=0.5做高斯滤波。

2、对每组（octave）倒数第三张图片做降采样，产生下组的第一层图片（第一组不用），由于降采样，越往上图片越小。

3、每层图片在上一层基础上做高斯滤波。

所谓尺度即一张图片的精细程度或概括度，用度量，

由下往上尺度变大。尺度用高斯函数中的方差来描述。

从2.1的高斯分布图可知，对一个区域做高斯滤波，若方差越大（峰越低），则这个点被平滑得越厉害，那么图像就变得越模糊。在模糊的图片中我们看到的是更宏观的东西（大，尺度大），而清晰的图片看到的是更为微观的东西（小，尺度小）。

点->线，边缘，角点->轮廓形状->鼻子，嘴巴->头->人（尺度由小到大）

组（O，octave），层（S），尺度（）三者的关系：

可见逐组逐层递增。

二、尺度空间上的关键点选取

关键点，即金字塔上的三维局部极值点。（三维：x，y，，每张图上的位置及图的尺度）

1、首先对gaussian做高斯差分（Difference of Gaussian，DOG）

即上层减下层。

原因：2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数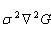的极大值和极小值同其它的特征提取函数，例如：梯度，Hessian或Harris角特征比较，能够产生最稳定的图像特征。而Lindeberg早在1994年就发现高斯差分函数（Difference of Gaussian ，简称DOG算子）与尺度归一化的高斯拉普拉斯函数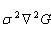非常近似。

所以用DOG之后提取的极值更有效。从而金字塔变成：

2、关键点定位

取三维极值点。

用到了两个trick

（1）子像素插值（Sub-pixel Interpolation），找到连续空间上的精确极值点。

（2）消除边缘效应，DOG算子会产生较强的边缘响应。

3、关键点方向

在每个找到的关键点的二维邻域内取方向梯度直方图，数值最大的方向作为该关键点的方向。

三、关键点的特征描述

每个关键点用一个向量来描述。

描述的方法就是取这个关键点在二维领域空间内的梯度值，

（1）取该点周围的4×4个区域，每个区域内含多个像素点

（2）每个区域的坐标轴旋转到该关键点的主方向上

（3）将子区域内的像素点的梯度值分配到8个方向上，计算其权值。

这样对于一个关键点，有4× 4× 8 = 128特征值。

SIFT的产生就是这样，对于一张输入图片，假设对其找到了K个关键点，他就有K× 128维的SIFT特征。