加密算法 - RSA

• 与DES不同，RSA算法中，每个通信主体都有两个钥匙，一个公钥一个私钥。

就是有2把钥匙
1。使用publicKey可以对数据进行加密
2。使用Key才能对数据进行解密
单方向传输
用公钥加密的数据，只有私钥能解开（可用于加密）；
同时，使用私钥加密的数据，只有公钥能解开（签名）。但是速度很慢（比私钥加密慢100到1000倍），
公钥的主要算法有RSA，还包括Blowfish,Diffie-Helman等

公钥与私钥
1.权威数字认证机构（CA）给所有通信主体（个人或组织）颁发公钥和私钥，彼此配对，分别唯一。
2.私钥好比数字指纹，同时具有解密和加密功能。个人保管，不公开。
3.公钥好比安全性极高的挂号信箱地址，公开。

公私钥加解密举例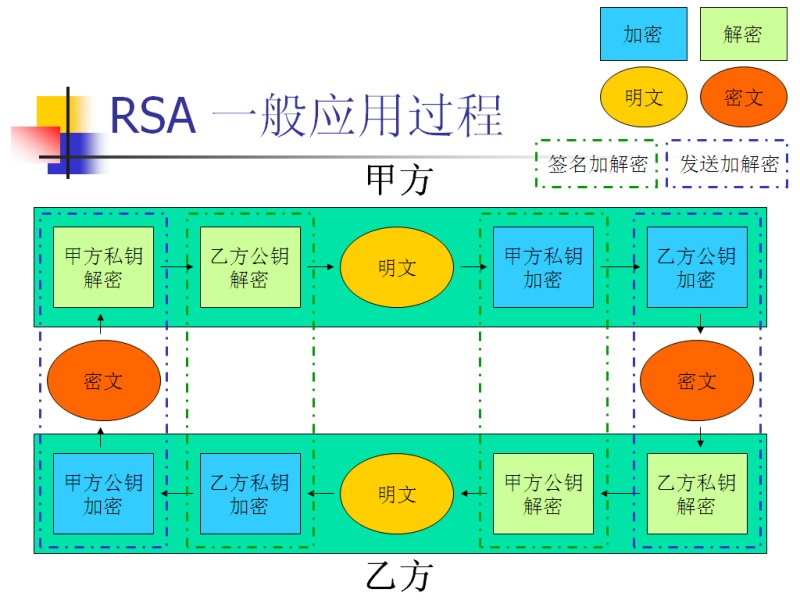设若甲有一份需保密的数字商业合同发给乙签署。经过如下步骤：
 1. 甲用乙的公钥对合同加密。
 2. 密文从甲发送到乙。
 3. 乙收到密文，并用自己的私钥对其解密。
 4. 解密正确，经阅读，乙用自己的私钥对合同进行签署。
 5. 乙用甲的公钥对已经签署的合同进行加密。
 6. 乙将密文发给甲。
 7. 甲用自己的私钥将已签署合同解密。
 8. 解密正确，确认签署。

公私钥加解密说明
从以上步骤，我们知道：
 1. 用公钥加密的密文能且只能用与其唯一配对的私钥才能解开。
 2. 如果某份密文被解开，那么肯定是密文的目标信息主体解开的。
 3. 私钥因其唯一标识所有者的属性，被用于数字签名，具有法律效力。

一。 公私钥生成
1.随机选定两个大素数p, q.
2.计算公钥和私钥的公共模数 n = pq .
3.计算模数n的欧拉函数 φ(n) .
4.选定一个正整数e, 使1 < e < φ(n) , 且e与φ(n)互质.
5.计算d, 满足 de ≡ 1  (mod φ(n) ), (k为某个正整数).
6.n与e决定公钥, n与d决定私钥.

二。加解密
该过程为小张给小李发消息，公钥为小李的公钥(n & e), 私钥为小李的私钥(n & d).
1.小张欲给小李发一个消息M, 他先把M转换为一个大数m < n, 然后用小李的公钥(n & e)把m加密为另一个大数: 
  c = me    mod n
2.小李收到小张发来的大数c, 着手解密. 通过自己的私钥(n & d), 得到原来的大数m: 
  m = cd    mod n
3.再把m转换为M, 小李即得到小张的原始消息.

这个过程之所以能通过, 是因为有如下等式: 
  cd ≡(me)d ≡med    (mod n)

RSA详细算法如下：

1、RSA算法

　　它是第一个既能用于数据加密也能用于数字签名的算法。它易于理解和操作，也很流行。算法的名字以发明者的名字命名：Ron Rivest, Adi Shamir 和Leonard Adleman。但RSA的安全性一直未能得到理论上的证明。它经历了各种攻击，至今未被完全攻破。

一、RSA算法 :

首先, 找出三个数, p, q, r, 
其中 p, q 是两个相异的质数, r 是与 (p-1)(q-1) 互质的数...... 
p, q, r 这三个数便是 private key 
 
接著, 找出 m, 使得 rm == 1 mod (p-1)(q-1)..... 
这个 m 一定存在, 因为 r 与 (p-1)(q-1) 互质, 用辗转相除法就可以得到了..... 
再来, 计算 n = pq....... 
m, n 这两个数便是 public key 
 
编码过程是, 若资料为 a, 将其看成是一个大整数, 假设 a < n.... 
如果 a >= n 的话, 就将 a 表成 s 进位 (s <= n, 通常取 s = 2^t), 
则每一位数均小於 n, 然後分段编码...... 
接下来, 计算 b == a^m mod n, (0 <= b < n), 
b 就是编码後的资料...... 
 
解码的过程是, 计算 c == b^r mod pq (0 <= c < pq), 
於是乎, 解码完毕...... 等会会证明 c 和 a 其实是相等的  :) 
 
如果第三者进行窃听时, 他会得到几个数: m, n(=pq), b...... 
他如果要解码的话, 必须想办法得到 r...... 
所以, 他必须先对 n 作质因数分解......... 
要防止他分解, 最有效的方法是找两个非常的大质数 p, q, 
使第三者作因数分解时发生困难......... 
 
 
<定理> 
若 p, q 是相异质数, rm == 1 mod (p-1)(q-1), 
a 是任意一个正整数, b == a^m mod pq, c == b^r mod pq, 
则 c == a mod pq 
 
证明的过程, 会用到费马小定理, 叙述如下: 
m 是任一质数, n 是任一整数, 则 n^m == n mod m 
(换另一句话说, 如果 n 和 m 互质, 则 n^(m-1) == 1 mod m) 
运用一些基本的群论的知识, 就可以很容易地证出费马小定理的........ 
 
<证明> 
因为 rm == 1 mod (p-1)(q-1), 所以 rm = k(p-1)(q-1) + 1, 其中 k 是整数 
因为在 modulo 中是 preserve 乘法的 
(x == y mod z  and  u == v mod z  =>  xu == yv mod z), 
所以, c == b^r == (a^m)^r == a^(rm) == a^(k(p-1)(q-1)+1) mod pq 
 
1. 如果 a 不是 p 的倍数, 也不是 q 的倍数时, 
   则 a^(p-1) == 1 mod p (费马小定理)  =>  a^(k(p-1)(q-1)) == 1 mod p 
      a^(q-1) == 1 mod q (费马小定理)  =>  a^(k(p-1)(q-1)) == 1 mod q 
   所以 p, q 均能整除 a^(k(p-1)(q-1)) - 1  =>  pq | a^(k(p-1)(q-1)) - 1 
   即 a^(k(p-1)(q-1)) == 1 mod pq 
   =>  c == a^(k(p-1)(q-1)+1) == a mod pq 
 
2. 如果 a 是 p 的倍数, 但不是 q 的倍数时, 
   则 a^(q-1) == 1 mod q (费马小定理) 
   =>  a^(k(p-1)(q-1)) == 1 mod q 
   =>  c == a^(k(p-1)(q-1)+1) == a mod q 
   =>  q | c - a 
   因 p | a 
   =>  c == a^(k(p-1)(q-1)+1) == 0 mod p 
   =>  p | c - a 
   所以, pq | c - a  =>  c == a mod pq 
 
3. 如果 a 是 q 的倍数, 但不是 p 的倍数时, 证明同上 
 
4. 如果 a 同时是 p 和 q 的倍数时, 
   则 pq | a 
   =>  c == a^(k(p-1)(q-1)+1) == 0 mod pq 
   =>  pq | c - a 
   =>  c == a mod pq 
                                        Q.E.D. 
 
 
这个定理说明 a 经过编码为 b 再经过解码为 c 时, a == c mod n  (n = pq).... 
但我们在做编码解码时, 限制 0 <= a < n, 0 <= c < n, 
所以这就是说 a 等於 c, 所以这个过程确实能做到编码解码的功能.....

二、RSA 的安全性

RSA的安全性依赖于大数分解，但是否等同于大数分解一直未能得到理论上的证明，因为没有证明破解 RSA就一定需要作大数分解。假设存在一种无须分解大数的算法，那它肯定可以修改成为大数分解算法。目前， RSA 的一些变种算法已被证明等价于大数分解。不管怎样，分解n是最显然的攻击方法。现在，人们已能分解多个十进制位的大素数。因此，模数n 必须选大一些，因具体适用情况而定。

三、RSA的速度

由于进行的都是大数计算，使得RSA最快的情况也比DES慢上倍，无论是软件还是硬件实现。速度一直是RSA的缺陷。一般来说只用于少量数据加密。

四、RSA的选择密文攻击

RSA在选择密文攻击面前很脆弱。一般攻击者是将某一信息作一下伪装( Blind)，让拥有私钥的实体签署。然后，经过计算就可得到它所想要的信息。实际上，攻击利用的都是同一个弱点，即存在这样一个事实：乘幂保留了输入的乘法结构：

( XM )^d = X^d *M^d mod n

前面已经提到，这个固有的问题来自于公钥密码系统的最有用的特征--每个人都能使用公钥。但从算法上无法解决这一问题，主要措施有两条：一条是采用好的公钥协议，保证工作过程中实体不对其他实体任意产生的信息解密，不对自己一无所知的信息签名；另一条是决不对陌生人送来的随机文档签名，签名时首先使用One-Way HashFunction 对文档作HASH处理，或同时使用不同的签名算法。在中提到了几种不同类型的攻击方法。

五、RSA的公共模数攻击

若系统中共有一个模数，只是不同的人拥有不同的e和d，系统将是危险的。最普遍的情况是同一信息用不同的公钥加密，这些公钥共模而且互质，那末该信息无需私钥就可得到恢复。设P为信息明文，两个加密密钥为e1和e2，公共模数是n，则：

C1 = P^e1 mod n

C2 = P^e2 mod n

密码分析者知道n、e1、e2、C1和C2，就能得到P。

因为e1和e2互质，故用Euclidean算法能找到r和s，满足：

r * e1 + s * e2 = 1

假设r为负数，需再用Euclidean算法计算C1^(-1)，则

( C1^(-1) )^(-r) * C2^s = P mod n

另外，还有其它几种利用公共模数攻击的方法。总之，如果知道给定模数的一对e和d，一是有利于攻击者分解模数，一是有利于攻击者计算出其它成对的e’和d’，而无需分解模数。解决办法只有一个，那就是不要共享模数n。

RSA的小指数攻击。 有一种提高 RSA速度的建议是使公钥e取较小的值，这样会使加密变得易于实现，速度有
所提高。但这样作是不安全的，对付办法就是e和d都取较大的值。

RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。RSA是被研究得最广泛的公钥算法，从提出到现在已近二十年，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何，而且密码学界多数人士倾向于因子分解不是NPC问题。

RSA的缺点主要有：

A)产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密。

B)分组长度太大，为保证安全性，n 至少也要 600 bits 以上，使运算代价很高，尤其是速度较慢，较对称密码算法慢几个数量级；且随着大数分解技术的发展，这个长度还在增加，不利于数据格式的标准化。目前，SET( Secure Electronic Transaction )协议中要求CA采用比特长的密钥，其他实体使用比特的密钥。

demo时刻,demo详见我的github<> 点击下载源码