CodeForces 540E - Gerald and Giant Chess（数论）

给一个棋盘，需要从左上角走到右下角，有部分点不能走，求一共有多少种走法。

首先要知道从一个点A到另一个点B在没有障碍下有多少种走法。保证A在B的左上方，如图

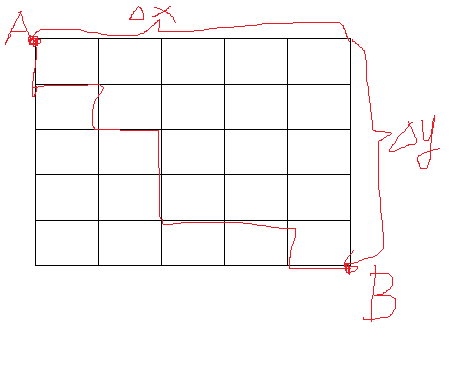
一共需要走(X+Y)步(图中△x，△y)，在其中选取X步走横向，Y步走竖向。所以一共有C(x+y, x)种走法。

把所有不能走的点排好序，对于每个点求出原点到该点的走法减去所有需要经过黑点的路径就是到该点的走法。

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const ll MOD = 1000000007;

const int MAX_P = 200005;

ll powMod(ll a, ll b, ll mod)
{
    ll res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

ll fac[MAX_P];
void getFact()
{
    fac[0] = 1;
    for (int i = 1; i <= 200000; ++i)
        fac[i] = fac[i - 1] * i % MOD;
}

ll Lucas(ll n, ll m, ll p)
{
    ll res = 1;
    while (n && m) {
        ll a = n % p;
        ll b = m % p;
        if (a < b) return 0;
        res = res * fac[a] * powMod(fac[b] * fac[a - b] % p, p - 2, p) % p;
        n /= p;
        m /= p;
    }
    return res;
}

struct Point {
    int x, y;
    Point(int x, int y):x(x),y(y){}
    Point(){}
    bool operator<(const Point a) const
    {
        if (x == a.x) return y < a.y;
        return x < a.x;
    }
} p[2005];

ll way(Point a, Point b)
{
    return Lucas(b.y - a.y + b.x - a.x, b.y - a.y, MOD);
}

ll ans[2005];
int main()
{
    int h, w, n;
    getFact();
    while (cin >> h >> w >> n) {
        Point s(1, 1);
        for (int i = 0; i < n; ++i) scanf("%d%d", &p[i].x, &p[i].y);
        p[n].x = h, p[n].y = w;
        sort(p, p + n);
        for (int i = 0; i <= n; ++i) {
            ans[i] = way(s, p[i]);
            for (int j = 0; j < i; ++j) {
                if (p[j].x <= p[i].x && p[j].y <= p[i].y) {
                    ans[i] = (ans[i] - way(p[j], p[i]) * ans[j]) % MOD;
                }
            }
        }
        ans[n] = (ans[n] + MOD) % MOD;
        printf("%lld\n", ans[n]);
    }
    return 0;
}