sorting--codility

lesson 6: sorting

lesson 6: sorting

exercise

Problem:

You are given a zero-indexed array A consisting of n > 0 integers; you must return the number of unique values in array A.

Solution O(nlogn):

First, sort array A; similar values will then be next to each other. Finally, just count the number of distinct pairs in adjacent cells.

def distinct(A):

	n = len(A)

	A.sort()

	result = 1

	for k in xrange(1, n):

		if A[k] != A[k - 1]: result += 1

	return result

The time complexity is O(n log n), in view of the sorting time.

1. Distinct

Compute number of distinct values in an array.

将list保存为set 即可
Test score 100%
也可以排序，然后对不同数进行计数，如exercise那样

def solution(A):

    # write your code in Python 2.7

    Aset = set(A)

    return len(Aset)

2. Triangle

Determine whether a triangle can be built from a given set of edges.

https://codesays.com/2014/solution-to-triangle-by-codility/

On one hand, there is no false triangular. Since the array is sorted, we already know A[index] < = A[index+1] <= A[index+2], and all values are positive. A[index] <= A[index+2], so it must be true that A[index] < A[index+1] + A[index+2]. Similarly, A[index+1] < A[index] + A[index+2]. Finally, we ONLY need to check A[index]+A[index+1] > A[index+2] to confirm the existence of triangular.

On the other hand, there is no underreporting triangular. If the inequality can hold for three out-of-order elements, to say, A[index]+A[index+m] > A[index+n], where n>m>1. Again, because the array is sorted, we must have A[index] < = A[index+m-1] and A[index+m+1] <= A[index + n]. So A[index+m-1] +A[index+m] >= A[index]+A[index+m] > A[index+n] >= A[index+m+1]. After simplification, A[index+m-1] +A[index+m] > A[index+m+1]. In other words, if we have any inequality holding for out-of-order elements, we MUST have AT LEAST an inequality holding for three consecutive elements.

def solution(A):

    # write your code in Python 2.7

    length = len(A)

    if length < 3:

        return 0

    A.sort()

    for idx in xrange(0,length -2):

        if A[idx]+A[idx + 1] > A[idx + 2]:

            return 1

    return 0

3. MaxProductOfThree

Maximize A[P] * A[Q] * A[R] for any triplet (P, Q, R).

solution 1

O(N)
Test score 100% OJ test is O(N * log(N))
考虑到有负数存在，故乘积最大的三个数，会出现在两种情况：
- 三个数均是正数，且是三个最大的数
- 两个负数和一个正数，最大正数和最小的两个负数

def solution(A):

    ma1, ma2, ma3 = -1000, -1000, -1000

    mi1, mi2 = 1000, 1000

    for elem in A:

        if elem > ma1:

            ma1, ma2, ma3 = elem, ma1, ma2

        elif elem > ma2:

            ma2, ma3 = elem, ma2

        elif elem > ma3:

            ma3 = elem

        if elem < mi1:

            mi1,mi2 = elem, mi1

        elif elem < mi2:

            mi2 = elem

    a, b = ma1*ma2*ma3, ma1*mi1*mi2

    return a if a > b else b

solution 2

note:

just need return the value of the max product,
基于解法一，我们可以先排序，然后直接取，不需要每个比较，相对来说，时间成本稍大
so, we can just consider the first or last teiplet, after sort
Detected time complexity: O(N * log(N))

def solution(A):

    A.sort()

    return max(A[0]*A[1]*A[-1], A[-1]*A[-2]*A[-3])

4. NumberOfDiscIntersections

We draw N discs on a plane. The discs are numbered from 0 to N − 1. A zero-indexed array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

  A[0] = 1

  A[1] = 5

  A[2] = 2

  A[3] = 1

  A[4] = 4

  A[5] = 0

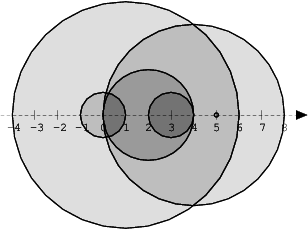
There are eleven (unordered) pairs of discs that intersect, namely:

discs 1 and 4 intersect, and both intersect with all the other discs;
disc 2 also intersects with discs 0 and 3.

problem:

Compute the number of intersections in a sequence of discs.

given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Assume that:

N is an integer within the range [0..100,000];
each element of array A is an integer within the range [0..2,147,483,647].

Complexity:

expected worst-case time complexity is O(N*log(N));
expected worst-case space complexity is O(N).

思路：

参考csdn
stackoverflow

initially we calculate all start and end points of discs. After go by all line and check count of discs inside current point. If in current point started some discs and intersection count increased by: already active distsc multiplied by count of started in current point (result += t * dps[i]) and count of intersections of started(result += dps[i] * (dps[i] - 1) / 2) eg. if started 5 discs in one of point it will increased by(1+2+3+4+5 intersections, or 5*(5-1) / 2[sum formula]).
构造成区间，[i-A[i],i+A[i]]
- e.g. A ＝［1，5，2，1，4，0］
- => [－1,1],[-4,6],[0,4],[2,4],[0,8],[5,5]
因为我们圆的中心位置在［0，len(A)],e.g. 在上例中 [0,5], 所以起点数组dps计算［0，i-A[i]］的范围，故有max(0,i-A[i])
终点数组不要超过每个圆心的最大值，即小于len（A）－1，故有min（length－1，i+A［i］）

sloution:[100%]

def solution(A):

    result = 0

    length = len(A)

    dps = [0]*length

    dpe = [0]*length

    for i in xrange(length):

        dps[max(0, i-A[i])] += 1

        dpe[min(length-1, i+A[i])] += 1

    tmp = 0

    for i in xrange(length):

        if dps[i] > 0:

            result += tmp*dps[i]

            result += dps[i] * (dps[i] - 1)/2

            if result > 10000000:

                return -1

            tmp += dps[i]

        tmp -= dpe[i]

    return result