字符串模式匹配算法1 - BF和KMP算法

在字符串S中定位/查找某个子字符串P的操作，通常称为字符串的模式匹配，其中P称为模式串。模式匹配有多种算法，这里先总结一下BF算法和KMP算法。

注意：本文在讨论字符位置/指针/下标时，全部使用C语法，即下标从0开始。

BF算法

BF（Brute Force)算法也就是传说中的“笨办法”，是一个暴力/蛮力算法。设串S和P的长度分别为m,n，则它在最坏情况下的时间复杂度是O(m*n)。BF算法的最坏时间复杂度虽然不好，但它易于理解和编程，在实际应用中，一般还能达到近似于O(m+n)的时间度（最坏情况不是那么容易出现的，RP问题），因此，还在被大量使用。

下面举例来说明BF算法的思想。

设S=‘ababcabcacbab’， P=‘abcac’，从S的第1个字符开始，依次比较S和P中的字符，如果没有完全匹配，则从S第2个字符开始，再次比较...如此重复，直到找到P的完全匹配或者不存在匹配。用数学语言描述，就是比较S_iS_i+1...S_i+n-1和P₀P₁...P_n-1，如果出现不匹配，则令i=i+1，继续这一过程，直到全部匹配，或者i>(m-n)。匹配过程如下（红色字体表示本趟比较中不匹配的字符）：

第1趟
S: a b a b c a b c a c b a b
P: a b c

第2趟
S: a b a b c a b c a c b a b
P:   a

第3趟
S: a b a b c a b c a c b a b
P:     a b c a c

第4趟
S: a b a b c a b c a c b a b
P:       a

第5趟

S: a b a b c a b c a c b a b
P:         a

第6趟

S: a b a b c a b c a c b a b
P:           a b c a c

以下是实现与测试的C代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// BF (Brute Force) algorithm
// worst time complexity : O(m*n)
static int bf (const char*, const char*);
static int bf2(const char*, const char*);

int main(void)
{
    char* str = "ababcabcacbab";
    char* ptn = "abcac";

    printf("match1 at %d\n", bf(str, ptn));
    printf("match2 at %d\n", bf2(str, ptn));

    return ;
}

int bf(const char* _str, const char* _ptn)
{
    int m, n, i, j;

    m = strlen(_str);
    n = strlen(_ptn);

    i = ; j = ;
    while(i<m && j<n)
    {
        if(_str[i] == _ptn[j])
        {
            printf("OK %d %d %c %c\n", i, j, _str[i], _ptn[j]);
            ++i;  ++j;
        }
        else
        {
            printf("NO %d %d %c %c\n", i, j, _str[i], _ptn[j]);
            i = i-j+; j = ;
        }
    }

    if(j >= n)
        return i-n;
    else
        return -;
}

int bf2(const char* _str, const char* _ptn)
{
    int m, n, i, j;

    m = strlen(_str);
    n = strlen(_ptn);

    i = ; j = ;
    for(i=; i<=(m-n); ++i)
    {
        for(j=; j<n; ++j)
        {
            if(_str[i+j] != _ptn[j])
            {
                printf("NO %d %d %c %c\n", i+j, j, _str[i+j], _ptn[j]);
                break;
            }
            else
                printf("OK %d %d %c %c\n", i+j, j, _str[i+j], _ptn[j]);
        }
        if(n == j)  return i;
    }

    return -;
}

BF算法的问题

BF算法在某些情况下存在效率上的问题。比如当S=‘aaaaaaabab’, P=‘aaab’时，BF算法匹配如下：

第1趟
S: a a a a a a a b a b
P: a a a b

第2趟
S: a a a a a a a b a b
P:   a a a b

第3趟
S: a a a a a a a b a b
P:     a a a b

第4趟
S: a a a a a a a b a b
P:       a a a b

第5趟
S: a a a a a a a b a b
P:         a a a b

若以i,j分别代表S串和P串当前比较的字符的位置/指针，那么(结合bf2函数))可以看出BF算法在每一趟匹配失败后，i,j均要回退——j回退到0，i回退到i-j+1——再继续下一趟比较（注意这里的i不是bf2函数里的i，而是相当于i+j）。而对以上特例来说，比如在第1趟比较后，S₃!=P₃事实上我们已经知道S₁S₂==‘aa’，因此不需要回退i，比较S₁和P₀, S₂和P₀，而只需回退j，比较S₃和P₂。这样的话，由于i没有回退，也就是减少了bf2中的外层循环次数，从而提高了匹配效率。如下图所示，图中↓表示当前指针i的位置。

↓
S: a a a a a a a b a b
P: a a a b       
         ->           
           ↓
S: a a a a a a a b a b
P:   a a a b                 
         ->             
             ↓
S: a a a a a a a b a b
P:     a a a b                       
         ->               
               ↓
S: a a a a a a a b a b
P:       a a a b       
         ->                 
                 ↓
S: a a a a a a a b a b
P:         a a a b

KMP算法

上面的改进算法就是KMP算法，它是由D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。KMP算法可以在O(m+n)的时间里完成串的模式匹配。它的主要思想是：每当一趟匹配过程中出现字符不匹配时，不需回退i指针，而是利用已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的一段距离后，继续匹配过程。

仍以一开始的例子S=‘ababcabcacbab’， P=‘abcac’来再看一遍KMP算法的匹配过程：

第1趟
            ↓ i=2
S: a b a b c a b c a c b a b
P: a b c

第2趟
                         ↓ i=6
S: a b a b c a b c a c b a b
P:     a b c a c

第3趟 
                                    ↓ i=10
S: a b a b c a b c a c b a b
P:          (a)b c a c

第1趟正常比较，S₂和P₂不匹配，而且发现S₁!=P₀，因此，第2趟比较时，就不需要比较S₁和P₀了，i指针保持不动，只需将j指针向右滑动1个位置，直接比较S₂和P₁即可；

第2趟比较时，S₆和P₄不匹配，而且发现S₃=='b'，S₄=='c'，均与P₀=='a'不匹配，因此，不需要进行以S₃与P₀、 S₄和P₀比较开始的这两趟。另外，又现S₅=='a'==P₀，因此，也不需要回退i指针，只需将j指针向右滑动一个位置，直接比较P₆与P₁即可。与本文开头的BF算法相比，KMP仅外层循环就减少为3趟，大大提升了匹配效率。

把上例的讨论推广到一般情况，设主串S=‘S₀S₁...S_m’，模式串P='P₀P₁...P_n'，那么我们要解决的问题可表述为：当匹配过程中产生“失配”（即不相等)时，模式串“向右滑动”的距离应该是多少？或者说，当S_i!=P_j时，S_i应该和P中的哪个字符继续比较？注意，主串的字符指针i不回退。

假设此时S_i应和P_k（k<j）继续比较，则k必满足以下条件，且k是满足此条件的最大值，即不存在k'(k<k'<j)也满足此条件：

P₀P₁...P_k-1 == S_i-kS_i-k+1...S_i-1               (1)

此时实际已得到的“部分匹配”结果是：

P_j-kP_j-k+1...P_j-1 == S_i-kS_i-k+1...S_i-1          (2)

由（1）、（2）两式，可推得：

P₀P₁...P_k-1== P_j-kP_j-k+1...P_j-1                          (3)

反过来讲，如果在匹配过程中，有S_i!=P_j，且有满足(3)式的k(k<j)存在时，则i不动，只需继续比较S_i和P_k即可；如果k不存在，则继续比较S_i和P₀。注意，k仅与模式P有关 ，而和主串S无关。

条件(3)表达了KMP算法的精髓之一。在主串指针i不移动的情况下，我们就是根据当前模式串指针j是否存在一个满足条件（3）的k，来决定模式串“向右滑动”的距离：

a.如果存在这个k，也就是说，失配的P_j前存在一个长度为k(0<k<j)的子串，它与模式串P开头的前k个字符组成的子串相同，或者叫“重叠”。而且，这个k是满足此条件的“最大的”k，如果使用了可能的“较小的”k进行继续比较，将会出现不必要的匹配过程。

b.如果k不存在，那么就从P₀开始继续比较。

要注意，如果存在_k，就必须比较P_k与S_i，不能比较P₀与S_i，否则将会出错。比如当：

S: a a a a a a a b a b
P:       a a a b

此时失配的i=6,j=3, 而k=2，(k需满足0<k<j)，下趟应比较S₆与P₂，如果无视k的存在，去比较S₆与P₀，就出错了，找不到匹配：

S: a a a a a a a b a b
P:             a a a b

从（3）式及其附近的表述，我们已经知道k的值与主串无关，仅与模式串本身有关，因此，我们可以把k表示为模式串位置/指针j的函数next(j)：

next(j) = Max {k | 0<k<j，且P₀P₁...P_k-1== P_j-kP_j-k+1...P_j-1 } ，k存在时
       或 = 0，k不存在时

举个例子，当P=‘abaabcac’时，其各位置的next值计算过程为：

a  j=0, next(j)=0
b  j=1, 满足0<k<1的整数k不存在，next(j)=0
a  j=2, 子串P₁ != P₀，k不存在，next(j)=0
a  j=3, 存在且仅存在子串P₂==P₀，next(j)=k=1
b  j=4, 存在且仅存在子串P₃==P₀，next(j)=k=1
c  j=5, 存在最大子串P₃P₄==P₀P₁，next(j)=k=2
a  j=6, 不存在要求子串，next(j)=0
c  j=7, 存在且仅存在子串P₆==P₀，next(j)=k=1

求得模式串的next函数后，KMP算法的匹配过程如下：

以指针i和j分别指示主串和模式串中当前要比较的字符，若在匹配过程中S_i==P_j，则i和j分别增1；否则，i不变（不回退），而j回退到next(j)，继续进行比较：若匹配，则i，j分别增1，否则，j继续回退到下一个next(j)，如此类推。直到以下两种可能：

• j回退到某个next(j)时 {next(next(...next(j)...)) }，S_i==P_j，则i,j分别增1；
• j退到0，即与模式串中第一个字符也不匹配，此时需要将i增1，j不变，即比较S_i+1和P_j。

KMP算法代码如下：

 int kmp(const char* _str, const char* _ptn)
 {
     size_t m = strlen(_str);
     size_t n = strlen(_ptn);
     size_t i = , j = ;

     size_t loop = ;

     int* next = (int*)malloc(n*sizeof(int));
     memset(next, , n*sizeof(int));
     //kmp_next(_ptn, next);
     kmp_next2(_ptn, next);

     for(i=; i<n; ++i)
         printf("%d ", next[i]);
     printf("\n");

     i = ; j = ;
     while(i < m && j < n)
     {
         loop++;
         if(_str[i] == _ptn[j])
             { ++i; ++j; }
         else if( == j)
             ++i;
         else
             j = next[j];
     }

     free(next); next = NULL;

     printf("loop: %ld\n", loop);

     if(j >= n)
         return i-n;
     else
         return -;
 }

求next函数值

求next(j)的一种方法是递推法。

首先由定义可知next(0) = 0。若令next(j) = k，则模式P中存在下列关系：

P₀P₁...P_k-1== P_j-kP_j-k+1...P_j-1   (1<k<j，且不存在k'>k满足此条件)

此时我们需要递推求得next(j+1)的值。分两种情形：

• 若P_k==P_j，则根据next函数定义，有next(j+1) == k+1 == next(j) + 1
• 若p_k!=P_j，这时可以应用KMP算法的思想，并把模式串本身既看成主串，又看成模式串，那么问题就转化成一般的KMP算法问题。根据KMP算法，这时，应把第next(k)个字符与P_j进行比较。若P_j==P_next(k) ，则next(j+1) == next(k)+1;若P_j != P_next(k)，则继续比较P_j和P_{next(next(k))} ......依此类推，直至P_j和某个字符匹配成功。或者不存在任何k'（1<k'<k<j)可以匹配成功，则令next(j+1)=0。

求next函数值的代码如下：

 void kmp_next(const char* _ptn, int* _next)
 {
     size_t n = strlen(_ptn);
     size_t i, j;

     if(n >= )
         _next[] = ;

     i = ; j = ;
     while(i < n)
     {
         if(_ptn[i] == _ptn[j])
             _next[++i] = ++j;
         else if( == j)
             _next[++i] = j;
         else
             j = _next[j];
     }
 }

next函数的改进

以上的next函数值求法对于某些情况会有一些不足。比如当S=‘aaabaaaab’，P=‘aaaab’时，进行到以下匹配：

S: a a a b a a a a b
P: a a a a b

发生失配S₃!=P₃。此时，如果按之前的next函数值求法，会得到next(1)==0, next(2)==1, next(3)==2，那么根据KMP算法，S₃会与P_next(3)即P₂进行比较；发现不匹配，那么模式串各右滑动，S₃继续与P_next(2)即P₁进行比较；发现还不匹配，继续向右滑动模式串，S₃继续与P_next(1)即P₀进行比较，发现仍不匹配，没办法，才会将S串上的i指针增1，让S₄与P₀比较。

然而，由于P₀,P₁,P₂和P₃相等，既然S₃!=P₃，那么根本没必要进行接下来的比较了，i指针可以直接增1，进行下边的比较。推广到一般情况来说，就是如果这样的情况发生，我们要人为地让j的回退幅度更大，以减少不必要的比较。 根据这个发现，我们可以对next函数的递推求值算法的情形1进行优化：

若P_k==P_next(j)==P_j时，恰满足P_k+1==P_next(j)+1==P_j+1，那么当P_j+1失配时，不需要比较P_next(j)+1和P_j+1，即next(j+1)不用取next(j)+1，而可以将模式串中要比较的位置再向左移，到next(j+1) = next(next(j+1))。

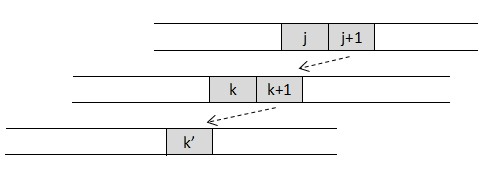
正如上图所示，由于P_j+1==P_k+1,next(j+1)的值可以跨过k+1，而直接到k'==next(k+1)，即next(j+1) = next(k+1) == next(next(j+1))。

改进后的next函数代码如下：

 void kmp_next2(const char* _ptn, int* _next)
 {
     size_t n = strlen(_ptn);
     size_t i, j;

     if(n >= )
         _next[] = ;

     i = ; j = ;
     while(i < n)
     {
         if(_ptn[i] == _ptn[j])
         {
             ++i; ++j;
             if(_ptn[i] != _ptn[j])
                 _next[i] = j;
             else
                 _next[i] = _next[j];
         }
         else if( == j)
             _next[++i] = j;
         else
             j = _next[j];
     }
 }

【参考资料】

《数据结构（C语言版）》，严蔚敏 吴伟民 编著，清华大学出版社。