KS检验学习[转载]

转自：https://wenku.baidu.com/view/ccfa573a3968011ca30091d6.html

https://www.cnblogs.com/arkenstone/p/5496761.html

1.定义

Kolmogorov-Smirnov是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|，当实际观测值D>D(n,α)则拒绝H0，否则则接受H0假设。
KS检验与t-检验之类的其他方法不同是KS检验不需要知道数据的分布情况，可以算是一种非参数检验方法。当然这样方便的代价就是当检验的数据分布符合特定的分布事，KS检验的灵敏度没有相应的检验来的高。在样本量比较小的时候，KS检验最为非参数检验在分析两组数据之间是否不同时相当常用。
PS：t-检验的假设是检验的数据满足正态分布，否则对于小样本不满足正态分布的数据用t-检验就会造成较大的偏差，虽然对于大样本不满足正态分布的数据而言t-检验还是相当精确有效的手段。

2.对单样本检验

3.两样本的KS检验

4.与卡方的比较

5.优势

2018-12-10更————

转自：https://www.cnblogs.com/arkenstone/p/5496761.html

1.KS原理

Kolmogorov-Smirnov是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。

其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|，当实际观测值D>D(n,α)则拒绝H0，否则则接受H0假设。
KS检验与t-检验之类的其他方法不同是KS检验不需要知道数据的分布情况，可以算是一种非参数检验方法。当然这样方便的代价就是当检验的数据分布符合特定的分布事，KS检验的灵敏度没有相应的检验来的高。在样本量比较小的时候，KS检验最为非参数检验在分析两组数据之间是否不同时相当常用。
PS：t-检验的假设是检验的数据满足正态分布，否则对于小样本不满足正态分布的数据用t-检验就会造成较大的偏差；

虽然对于大样本不满足正态分布的数据而言t-检验还是相当精确有效的手段。

2.KS工作流程

首先观察下分析数据
1.对于以下两组数据：
controlB={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}
treatmentB= {2.37, 2.16, 14.82, 1.73, 41.04, 0.23, 1.32, 2.91, 39.41, 0.11, 27.44, 4.51, 0.51, 4.50, 0.18, 14.68, 4.66, 1.30, 2.06, 1.19}

对于controlB，这些数据的统计描述如下：
Mean = 3.61
Median = 0.60
High = 50.6 Low = 0.08
Standard Deviation = 11.2
//可以发现这组数据并不符合正态分布，否则大约有15%的数据会小于均值-标准差（3.61-11.2），而数据中显然没有小于0的数。

2.观察数据的累计分段函数（Cumulative Fraction Function）
对controlB数据从小到大进行排序：
sorted controlB={0.08, 0.10, 0.15, 0.17, 0.24, 0.34, 0.38, 0.42, 0.49, 0.50, 0.70, 0.94, 0.95, 1.26, 1.37, 1.55, 1.75, 3.20, 6.98, 50.57}。10%的数据（2/20）小于0.15，85%（17/20）的数据小于3。所以，对任何数x来说，其累计分段就是所有比x小的数在数据集中所占的比例。下图就是controlB数据集的累计分段图

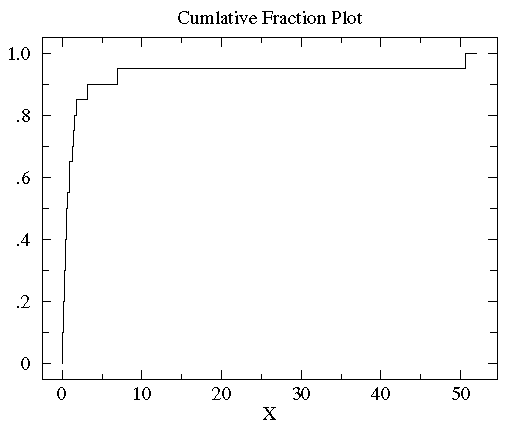
可以看到大多数数据都几种在图片左侧（数据值比较小），这就是非正态分布的标志。为了更好的观测数据在x轴上的分布，可以对x轴的坐标进行非等分的划分。在数据都为正的时候有一个很好的方法就是对x轴进行log转换。下图就是上图做log转换以后的图：

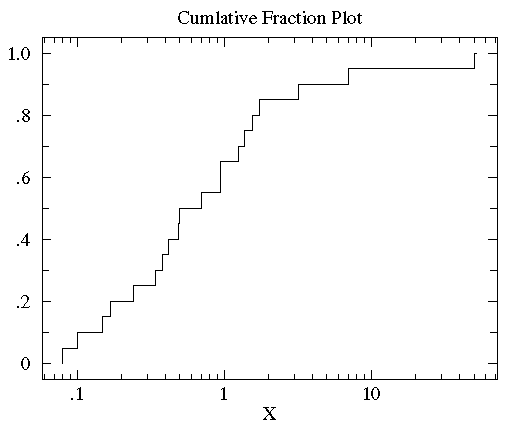
//其实看不太懂这个log转换

最终描述出controlB与treatmentB之间的图像：

D=0.45（0.65-0.25）。

那么在R中使用ks.test()函数，得到的结果：

Two-sample Kolmogorov-Smirnov test

data:  controlB and treatmentB

D = 0.45, p-value = 0.03354

alternative hypothesis: two-sided

这里p<0.05，说明原假设是两个是同一个分布，这里应该说明了两者就是同一分布，我又做了个实验。

> x<-rnorm(30)

> y<-rnorm(30)

> ks.test(x,y)

结果：

Two-sample Kolmogorov-Smirnov test

data:  x and y

D = 0.13333, p-value = 0.9578

alternative hypothesis: two-sided

//居然P值这么大，那么就否定原假设（二者是同样的分布），二者不是同样的分布。《-我理解错了这里！

应该是p值很大，不能否认原假设，证明二者来自同一分布。

//这就很尴尬了，明明就是正态分布啊。又做了一个检测：

> u1<-runif(30)

> u2<-runif(30)

> ks.test(u1,u2)

结果：

    Two-sample Kolmogorov-Smirnov test

data:  u1 and u2

D = 0.26667, p-value = 0.2391

alternative hypothesis: two-sided

//这也很尴尬了，这两个明明就是来自于同一分布，为什么显示P值还这么大。《-我理解错了这里！

说明p值很大，不能否认原假设，证明二者来自同一分布。

对于不属于同一分布的：

> ks.test(x,u1)

    Two-sample Kolmogorov-Smirnov test

data:  x and u1

D = 0.46667, p-value = 0.00253

alternative hypothesis: two-sided

p值倒是挺小。那么也就是说否认了原假设H0（二者来自同一分布），二者不来自同一分布。

下面还有讲到百分比图，那个我认为作用不大，就不放在这里了。