js串结构

朴素匹配算法

//S 主串 T 模式串

//匹配失败，回溯
i = i - j +  1
j = 0

//匹配成功，返回位置
i - j

function indexOf(S,T,pos = 0){
  let i = pos
  let j = 0;

  while(i <= S.length && j <= T.length){
    if(S[i] == T[j]){
      ++i
      ++j
    }else{
      //回溯
      i = i - j + 1
      j = 0
    }
  }

  if(j >= T.length){
    return i - j
  } else {
    return 0
  }
}

KMP算法

字符串前后缀

字符关系

A  B    C   A    B    B
0  k-1  k  j-k  j-1   j

执行过程

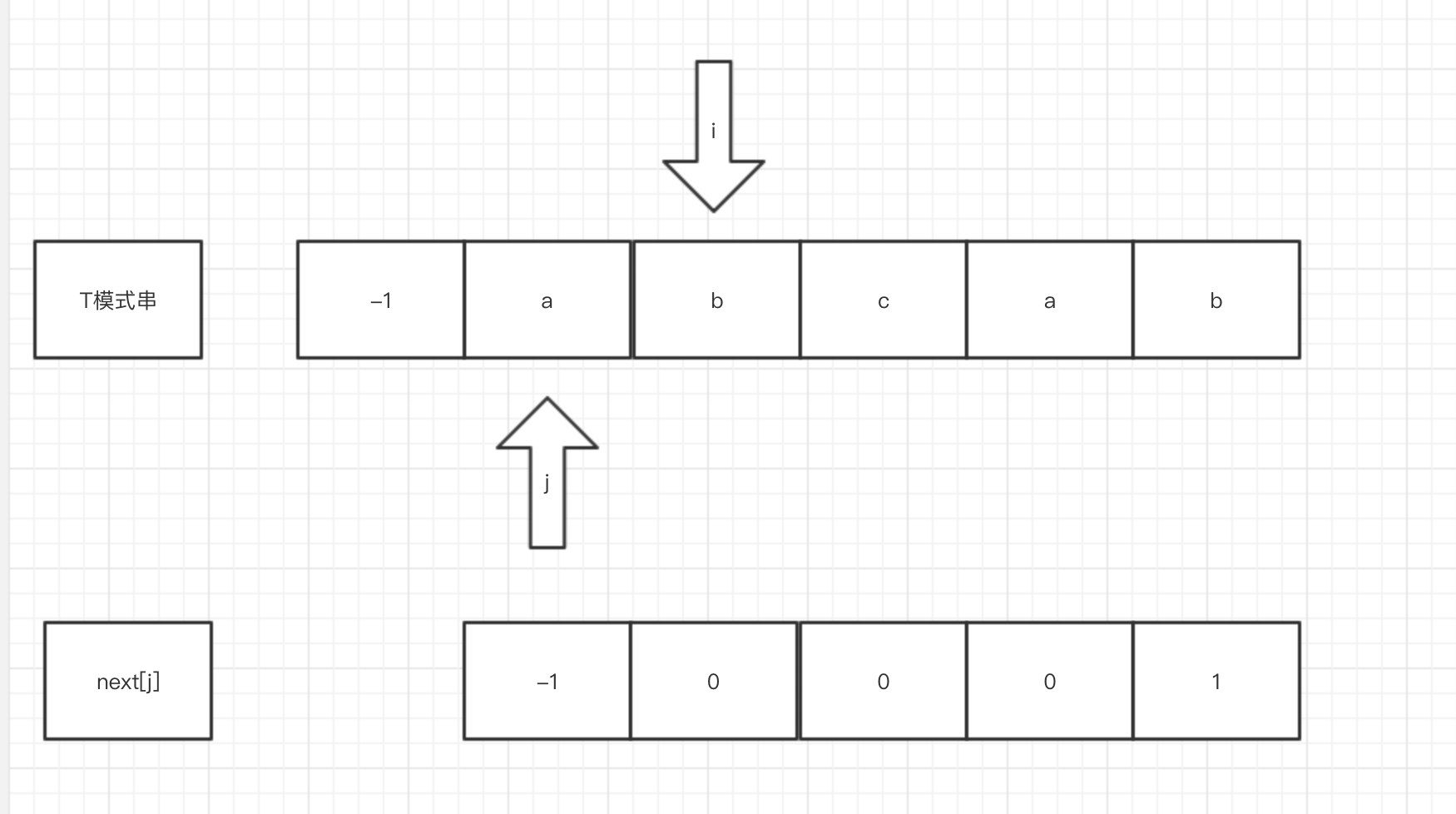
//i指针不必回溯
//next[j]表示回溯位置

/*
规则1:没有公共前后缀的情况，匹配失败时j = 0去匹配
s:    a b (c) d e f g
t:    a b (d)

t串中a与后边的bd串都不相等，在d匹配c失败时，可以知道t[a] = s[a], t[b] = s[b]，t[a] != t[b]，因此t[a] != s[b]

因为t[a] != t[b] != s[b]，所以不用比较t[a]与s[b]，只需要将a移动到匹配失败的位置即可

s:    a b (c) d e f g
t:        (a) b d

规则2：有公共前后缀的情况，匹配失败时j 根据当前字符串的前后缀相似度进行匹配

s:  a b c a b a b c a
t:  a b c a b x

因为t[a] != t[b] != s[b] != s[c]，所以匹配失败时不必比较s[b],s[c]

s: a b c a b a b c a
t:       a b c a b x

因为t[0],t[1] = t[3],t[4]，由于t[3],t[4] = s[3],s[4] = t[0],t[1]，所以也s[3],s[4]也不用比较

在于s串比较时，都是通过判断t串中有无重复的元素，来决定与s串的某一位置进行比较

next[j] = {
    0,当j = 1时，next[j] = 0
    Max:{k | 1 < k < j, 且 p1 - pk-1 = pj-k+1 - pj - 1}
    1,其他情况
}

现在的问题转移到当匹配失败时，如何计算出j的回溯位置 ? 

k值就是公共前后缀的长度，如果k = 1，那么就是k + 1 = 2

t = abcdex
n = next[j]

j: 1 2 3 4 5 6
t: a b c d e x
n: 0 1 1 1 1 1

j = 1，j是a，没有前后缀，next[1] = 0
j = 2，j是ab，1 到 j - 1时，只有字符a，没有公共前后缀，next[2] = 1
j = 3，j是abc，1 到 j - 1，没有公共前后缀，next[3] = 1
j = 4，j是abcd，1 到 j - 1 没有公共前后缀，next[4] = 1
最后结果：next[j] = [0,1,1,1,1,1]

当匹配失败时，调用next[j]，假设现在时j = 6匹配失败了，next[6] = 1, 那么我们应该回溯到j = 1 进行匹配，也就是t[1] = a

当有公共前后缀的情况
t = abcabx
n = next[j]

j: 1 2 3 4 5 6
t: a b c a b x
n: 0 1 1 1 2 3

j = 1，next[1] = 0
j = 2，1 到 j - 1的字符是a，next[2] = 1
j = 3，1 到 j - 1的字符是ab，next[3] = 1
j = 4，1 到 j - 1的字符是abc，next[4] = 1
j = 5，1 到 j - 1的字符是abca, 公共前后缀是a，next[5] = 2
j = 6, 1 到 j - 1的字符是abcab，公共前后缀是ab，next[6] = 3

当匹配失败时，j = 6，next[6] = 3，那么j回溯3去比较

j: 1 2 3 4 5 6 7 8 9
t: a b a b a a a b a
n: 0 1 1 2 3 4 2 2 3

当j = 1, next[1] = 0
当j = 2, next[2] = 1
当j = 3, next[3] = 1
当j = 4, 公共前后缀a，next[4] = 2
当j = 5，公共前后缀ab，next[5] = 3
当j = 6，公共前后缀aba，next[6] = 4
当j = 7，公共前后缀a，next[a] = 2
当j = 8，公共前后缀a，next[a] = 2
当j = 9，公共前后缀ab，next[a] = 3

当j = 9匹配失败时，next(9) = 3，j应该回溯到第j = 3的位置进行比较

j: 1 2 3 4 5 6 7 8 9
t: a a a a a a a a b
n: 0 1 2 3 4 5 6 7 8

j = 1, next[1] = 0
j = 2, next[2] = 1
j = 3, next[3] = 2
j = 4, next[4] = 3
j = 5, next[5] = 4
j = 6, next[6] = 5
j = 7, next[7] = 6
j = 8, next[8] = 7
j = 9, next[9] = 8

*/
function get_next(T,next = []){
  let i = 0;
  let j = -1;
  //第一个字符就匹配失败的情况
  next[0] = -1;

  while(i < T.length - 1){
   //假设没有前后缀，设置初始值，第二次循环在验证是不是真的没有前后缀
    if(j == -1 || T[i] == T[j]){
      //给没有公共前后缀和前后缀一致的字符添加回退索引
      ++i
      ++j
      next[i] = j
    }
    else {
      //根据失败位置索引，找到应该回退的索引
      j = next[j]
    }
  }

  return next
}
//进行修正
// s: aab
// t: aaa
//当a与b不匹配时，前面的a与后面的a是一样的没有必要在进行匹配
function get_nextval(T,nextval = []){
    let i = 1;
    nextval[1] = 0;
    let j = 0;

    while(i < T.length - 1){
        if(j == -1 || T[i] == T[j]){
            ++i
            ++j
            if(T[i] != T[j]){
                nextval[i] = j
            } else {
                //如果前后缀相同的情况
                //跳过层层回溯，直接回溯到开始位置
                nextval[i] = nextval[j]
            }
        } else { 

            j = nextval[j]
        }
    }
}

function kmp_search(S,T,pos = 0){
  let i = pos;
  let j = 0;
  let next = get_next(T)
  console.log(next)

  while( i < S.length && j < T.length){
    if(j === -1 || S[i] === T[j]){
      //j === -1 的时候将i向后移动的同时将j归0
      i++
      j++
    } else {
      j = next[j]
    }
  }

  if(j === T.length){
    return i - j
  }
  else {
    return -1
  }
}

//kmp另一种实现
function prefix_table(pattern = [],prefix = [],n){
    pattern[0] = 0
    let len = 0
    let i 

    while( i < n){
        if(pattern[i] == pattern[len]){
            len ++
            prefix[i] = len
            i ++
        }
        else {
            if(len > 0){
                len  = prefix[len - 1]
            } else {
                prefix[i] = len
                i ++
            }
        }
    }
}

function move_prefix_table(prefix = [],n){
    let i
    for(i = n - 1; i > 0; i--){
        prefix[i] = prefix[i - 1]
    }
    prefix[0] = -1
}

function kmp_search(text = [],pattern = []){
    let n = pattern.length
    let m  = text.length
    let prefix = []
    let i = 0
    let j = 0

    prefix_table(pattern,prefix,n)
    move_prefix_table(prefix,n)

    while( i < m){
        if( j == n - 1 && text[i] == pattenr[j]){
            console.log(i - j)
            j = prefix[j]
        }
        if(text[i] == pattern[j]){
            i++
            j++
        }
        else {
            j = prefix[j]
            if(j == -1){
                i++
                j++
            }
        }
    }
}