JS实现最小生成树之克鲁斯卡尔（Kruskal）算法

克鲁斯卡尔算法打印最小生成树：

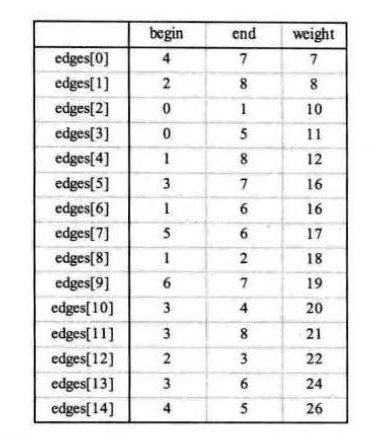
　　构造出所有边的集合 edges，从小到大，依次选出筛选边打印，遇到闭环（形成回路）时跳过。

JS代码：

 //定义邻接矩阵
 let Arr2 = [
     [0, 10, 65535, 65535, 65535, 11, 65535, 65535, 65535],
     [10, 0, 18, 65535, 65535, 65535, 16, 65535, 12],
     [65535, 18, 0, 22, 65535, 65535, 65535, 65535, 8],
     [65535, 65535, 22, 0, 20, 65535, 65535, 16, 21],
     [65535, 65535, 65535, 20, 0, 26, 65535, 7, 65535],
     [11, 65535, 65535, 65535, 26, 0, 17, 65535, 65535],
     [65535, 16, 65535, 65535, 65535, 17, 0, 19, 65535],
     [65535, 65535, 65535, 16, 7, 65535, 19, 0, 65535],
     [65535, 12, 8, 21, 65535, 65535, 65535, 65535, 0],
 ]

 let numVertexes = 9, //定义顶点数
     numEdges = 15; //定义边数

 // 定义图结构
 function MGraph() {
     this.vexs = []; //顶点表
     this.arc = []; // 邻接矩阵，可看作边表
     this.numVertexes = null; //图中当前的顶点数
     this.numEdges = null; //图中当前的边数
 }
 let G = new MGraph(); //创建图使用

 //创建图
 function createMGraph() {
     G.numVertexes = numVertexes; //设置顶点数
     G.numEdges = numEdges; //设置边数

     //录入顶点信息
     for (let i = 0; i < G.numVertexes; i++) {
         G.vexs[i] = 'V' + i; //scanf('%s'); //ascii码转字符 //String.fromCharCode(i + 65);
     }
     console.log(G.vexs) //打印顶点

     //邻接矩阵初始化
     for (let i = 0; i < G.numVertexes; i++) {
         G.arc[i] = [];
         for (j = 0; j < G.numVertexes; j++) {
             G.arc[i][j] = Arr2[i][j]; //INFINITY;
         }
     }
     console.log(G.arc); //打印邻接矩阵
 }

 function Edge() {
     this.begin = 0;
     this.end = 0;
     this.weight = 0;
 }

 function Kruskal() {
     let n, m;
     let parent = []; //定义一数组用来判断边与边是否形成环路
     let edges = []; //定义边集数组

     for (let i = 0; i < G.numVertexes; i++) {
         for (let j = i; j < G.numVertexes; j++) { //因为是无向图所以相同的边录入一次即可，若是有向图改为0
             if (G.arc[i][j] != 0 && G.arc[i][j] != 65535) {
                 let edge = new Edge();
                 edge.begin = i;
                 edge.end = j;
                 edge.weight = G.arc[i][j];
                 edges.push(edge);
             }
         }
     }

     edges.sort((v1, v2) => {
         return v1.weight - v2.weight
     });

     console.log('**********打印所有边*********');
     console.log(edges);

     for (let i = 0; i < G.numVertexes; i++) {
         parent[i] = 0;
     }

     for (let i = 0; i < edges.length; i++) {
         n = Find(parent, edges[i].begin)
         m = Find(parent, edges[i].end)
         if (n != m) { //假如n与m不等，说明此边没有与现有生成树形成环路
             parent[n] = m;
             console.log("(%s,%s) %d", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight);
         }
     }
 }

 function Find(parent, f) { //查找连线顶点的尾部下标
     while (parent[f] > 0) {
         f = parent[f]
     }
     return f;
 }

 createMGraph();
 console.log('*********打印最小生成树**********')
 Kruskal();

打印结果：

代码部分过程解析:

 

当i=7时，第82行，调用Find函数，会传入参数edges[7].begin=5。此时第94行，parent[5]=8>0,所以f=8，再循环得parent[8]=6。因parent[6]=0 所以Find返回后第82行得到n=6。而此时第83行，传入参数edges[7].end=6得到m=6。此时n=m，不再打印，继续下一循环。这就告诉我们，因为（V5,V6）使得边集合A形成了环路。因此不能将它纳入到最小生成树中。

当i=8时，与上面相同，由于边（V1,V2）使得边集合A形成了环路，因此不将它纳入最小生成树。

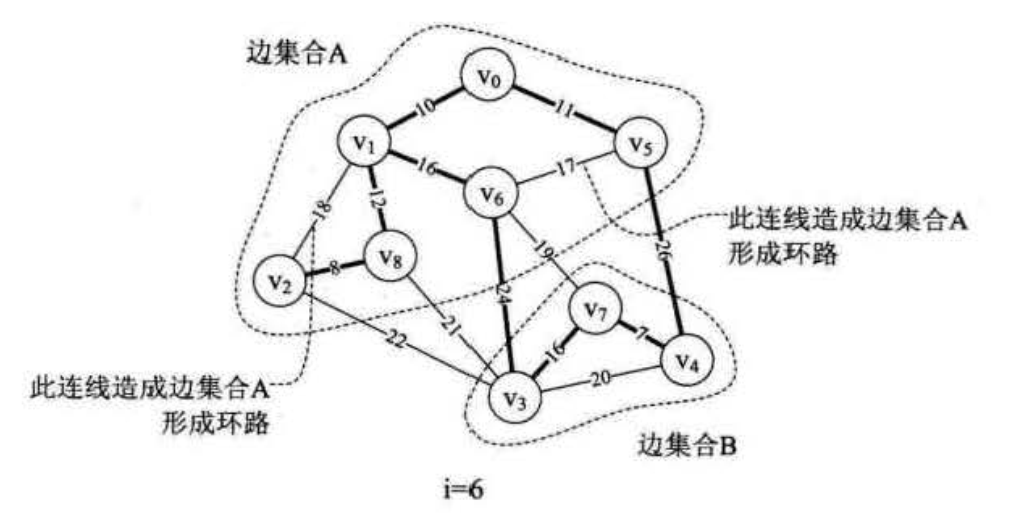
克鲁斯卡尔算法主要针对边展开，时间复杂度为 O(elog e)，e为图的边数，普利姆算法的时间复杂度为O(n²)，n为最小生成树的边数。所以，边数少（稀疏图）用克鲁斯卡尔算法，边数多（稠密图）用普利姆算法。

参考文献： 程杰《大话数据结构》