【noip2018】【luogu5024】保卫王国

题目描述

Z 国有nn座城市，n - 1n−1条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。

Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件：

一座城市可以驻扎一支军队，也可以不驻扎军队。
由道路直接连接的两座城市中至少要有一座城市驻扎军队。
在城市里驻扎军队会产生花费，在编号为i的城市中驻扎军队的花费是p_ipi。

小 Z 很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小 Z 提出了mm个要求，每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一给出回答。具体而言，如果国王提出的第jj个要求能够满足上述驻扎条件（不需要考虑第 jj 个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。如果国王提出的第jj个要求无法满足，则需要输出-1 (1 ≤ j ≤ m)−1(1≤j≤m)。现在请你来帮助小 Z。

输入输出格式

输入格式：

第 11 行包含两个正整数n,mn,m和一个字符串typetype，分别表示城市数、要求数和数据类型。typetype是一个由大写字母 AA，BB 或 CC 和一个数字 11，22，33 组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中有具体的描述。

第 22 行nn个整数p_ipi，表示编号ii的城市中驻扎军队的花费。

接下来 n - 1n−1 行，每行两个正整数u,vu,v，表示有一条uu到vv的双向道路。

接下来 mm 行，第jj行四个整数a,x,b,y(a ≠ b)a,x,b,y(a≠b)，表示第jj个要求是在城市aa驻扎xx支军队，在城市bb驻扎yy支军队。其中，xx 、 yy 的取值只有 00 或 11：若 xx 为 00，表示城市 aa 不得驻扎军队，若 xx 为 11，表示城市 aa 必须驻扎军队；若 yy为 00，表示城市 bb不得驻扎军队，若 yy为 11，表示城市 bb 必须驻扎军队。

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

输出格式：

输出共 mm 行，每行包含 11 个整数，第jj行表示在满足国王第jj个要求时的最小开销，如果无法满足国王的第jj个要求，则该行输出 -1−1。

输入输出样例

输入样例#1： 复制

输出样例#1： 复制

说明

【样例解释】

对于第一个要求，在 44 号和 55 号城市驻扎军队时开销最小。

对于第二个要求，在 11 号、22 号、33 号城市驻扎军队时开销最小。

第三个要求是无法满足的，因为在 11 号、55 号城市都不驻扎军队就意味着由道路直接连接的两座城市中都没有驻扎军队。

【数据规模与约定】

对于 100\%100%的数据，n,m ≤ 100000,1 ≤ p_i ≤ 100000n,m≤100000,1≤pi≤100000。

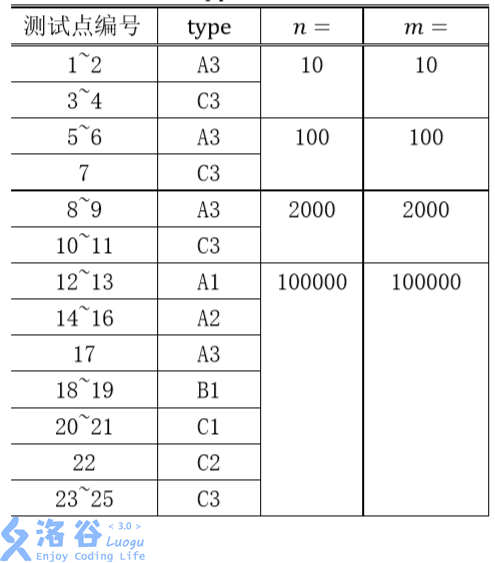
数据类型的含义：

AA：城市ii与城市i + 1i+1直接相连。
BB：任意城市与城市 11 的距离不超过 100100（距离定义为最短路径上边的数量），即如果这棵树以 11 号城市为根，深度不超过 100100。
CC：在树的形态上无特殊约束。
11：询问时保证a = 1,x = 1a=1,x=1，即要求在城市 11 驻军。对b,y没有限制。
22：询问时保证a,ba,b是相邻的（由一条道路直接连通）
33：在询问上无特殊约束。

题解：

首先一般的暴力$dp[u][0] = \sum dp[v][1]$ , $dp[u][1] = \sum min(dp[v][0],dp[v][1]) + a[u]$

复杂度$O(n^2)$

考虑倍增优化：

fa[u][i]表示u向上跳2^i的祖先，然后用f[u][i]表示以fa[u][i]为根节点，不包括u的子树的最优dp值；

将f[u][i]写成一个2*2的矩阵，表示fa[u][i]和u是否选择；

更新一个点u，直接从u倍增到根节点就可以了；

考虑同时更新u和v，先跳到他们lca的儿子，再从lca跳到根，分类合并一下三个矩阵；

注意特判v和u有祖先关系的情况；

LCT做法：
其实这东西似乎叫动态dp

一般套路是将转移写成矩阵然后用数据结构维护；

树链剖分后 f[u][0/1]表示u为根的子树dp值，g[u][0/1]表示u为根的子树除开重儿子($son_{u}$)的dp值；

$f[u][0] = g[u][0] + f[son_{u}][1] $ ,

$f[u][1] = g[u][1] + min( f[son_{u}][0] , f[son_{u}][1] ) $

将加法定义成取min，乘法定义成加法，转移写成矩阵：$$\\
\begin{pmatrix} f[son_{u}][0] & f[son_{u}][1] \end{pmatrix} \
\begin{pmatrix} \infty & g[u][1] \\ g[u][0] & g[u][1] \end{pmatrix}
=
\begin{pmatrix} f[u][0] & f[u][1] \end{pmatrix}
$$

用LCT维护(只写了倍增，后面补上)

另外推荐一个动态dp的题：http://noi.ac/problem/111

 #include<bits/stdc++.h>

 #define il inline

 #define rg register

 #define ll long long

 using namespace std;

 const int N=;

 ll inf=1e15;

 struct mat{

     ll c[][];

     mat(ll _a=inf,ll _b=inf,ll _c=inf,ll _d=inf){

         c[][]=_a;c[][]=_b;

         c[][]=_c;c[][]=_d;

     }

     mat operator *(const mat&A){

         mat ret;

         for(int i=;i<;i++)

         for(int j=;j<;j++){

             ret.c[i][j]=min(inf,min(c[i][]+A.c[][j],c[i][]+A.c[][j]));

         }

         return ret;

     }

 }f[N][];

 char gc(){

     static char*p1,*p2,s[];

     if(p1==p2)p2=(p1=s)+fread(s,,,stdin);

     return(p1==p2)?EOF:*p1++;

 }

 int rd(){

     int x=; char c=gc();

     while(c<''||c>'')c=gc();

     while(c>=''&&c<='')x=(x<<)+(x<<)+c-'',c=gc();

     return x;

 }

 int n,m,o,hd[N];

 ll a[N],dep[N],fa[N][],bin[],dp[N][];

 struct Edge{int v,nt;}E[N<<];

 void adde(int u,int v){

     E[o]=(Edge){v,hd[u]};hd[u]=o++;

     E[o]=(Edge){u,hd[v]};hd[v]=o++;

 }

 void dfs0(int u,int F){

     dp[u][]=;dp[u][]=a[u];

     for(rg int i=hd[u];~i;i=E[i].nt){

         int v=E[i].v;

         if(v==F)continue;

         dfs0(v,u);

         dp[u][]+=dp[v][];

         dp[u][]+=min(dp[v][],dp[v][]);

     }

 }

 void dfs(int u,int F){

     dep[u]=dep[fa[u][]=F]+;

     f[u][]=mat(

         inf,

         dp[fa[u][]][]-dp[u][],

         dp[fa[u][]][]-min(dp[u][],dp[u][]),

         dp[fa[u][]][]-min(dp[u][],dp[u][])

     );

     for(rg int i=;bin[i]<dep[u];i++){

         fa[u][i]=fa[fa[u][i-]][i-];

         f[u][i]=f[fa[u][i-]][i-]*f[u][i-];

     }

     for(rg int i=hd[u];~i;i=E[i].nt){

         int v=E[i].v;

         if(v==F)continue;

         dfs(v,u);

     }

 }

 void solve(int u,int x,int v,int y){

     if(dep[u]<dep[v])swap(u,v),swap(x,y);

     mat tu,tv,t;

     tu=mat(dp[u][],inf,inf,dp[u][]);

     tv=mat(dp[v][],inf,inf,dp[v][]);

     for(int i=;i<;i++)if(bin[i]&(dep[u]-dep[v])){

         tu=f[u][i]*tu;

         u=fa[u][i];

     }

     if(u==v){

         ll ans;

         t=mat(,inf,inf,);

         for(int i=;i<;i++)if(bin[i]&(dep[u]-)){

             t=f[u][i]*t;

             u=fa[u][i];

         }

         ans= min(t.c[][y],t.c[][y])+tu.c[y][x];

         if(ans>=inf)puts("-1");

         else printf("%lld\n",ans);

         return;

     }

     for(int i=;~i;i--)if(fa[u][i]!=fa[v][i]){

         tu=f[u][i]*tu;

         tv=f[v][i]*tv;

         u=fa[u][i];

         v=fa[v][i];

     }

     t=mat(

         dp[fa[u][]][]-dp[u][]-dp[v][],

         inf,

         inf,

         dp[fa[u][]][]-min(dp[u][],dp[u][])-min(dp[v][],dp[v][])

     );

     u=fa[u][];

     for(int i=;i<;i++)if(bin[i]&(dep[u]-)){

         t=f[u][i]*t;

         u=fa[u][i];

     }

     ll ans=inf;

     ans = min(

         min(t.c[][],t.c[][])+tu.c[][x]+tv.c[][y],

         min(t.c[][],t.c[][])+min(tu.c[][x],tu.c[][x])+min(tv.c[][y],tv.c[][y])

     );

     if(ans>=inf)puts("-1");

     else printf("%lld\n",ans);

 }

 int main(){

     freopen("defense.in","r",stdin);

     freopen("defense.out","w",stdout);

     n=rd(); m=rd(); gc(); gc();

     for(rg int i=bin[]=;i<;i++)bin[i]=bin[i-]<<;

     for(rg int i=;i<=n;i++)a[i]=rd(),hd[i]=-;

     for(rg int i=;i<n;i++)adde(rd(),rd());

     dfs0(,);

     dfs(,);

     for(rg int i=,u,v,x,y;i<=m;i++){

         u=rd();x=rd();v=rd();y=rd();

         solve(u,x,v,y);

     }

     return ;

 }

倍增