BZOJ5306 [HAOI2018]染色【组合数 + 容斥 + NTT】

题目

为了报答小 C 的苹果, 小 G 打算送给热爱美术的小 C 一块画布, 这块画布可以抽象为一个长度为 $N$ 的序列, 每个位置都可以被染成 $M$ 种颜色中的某一种.

然而小 C 只关心序列的 $N$ 个位置中出现次数恰好为 $S$ 的颜色种数, 如果恰好出现了 $S$ 次的颜色有 $K$ 种, 则小 C 会产生 $W_k$ 的愉悦度.

小 C 希望知道对于所有可能的染色方案, 他能获得的愉悦度的和对 1004535809 取模的结果是多少.

输入格式

从标准输入读入数据. 第一行三个整数 $N, M, S$.

接下来一行 $M + 1$ 个整数, 第 $i$ 个数表示 $W_{i-1}$

.

输出格式

输出到标准输出中. 输出一个整数表示答案．

输入样例

8 8 3

3999 8477 9694 8454 3308 8961 3018 2255 4910

输出样例

524070430

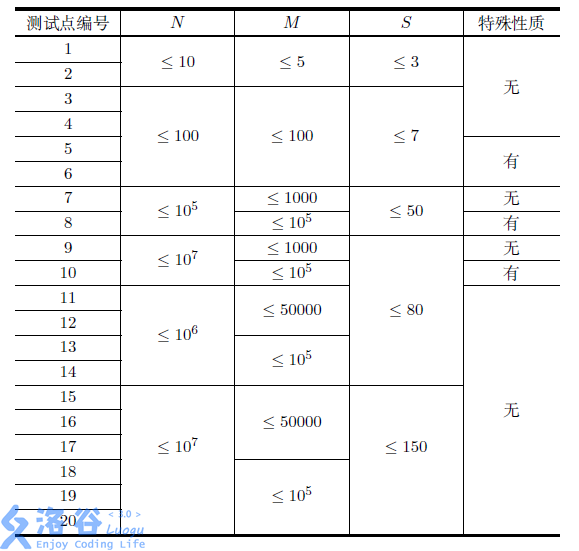
提示

特殊性质: $\forall 1 \le i \le m, W_i = 0$

对于 $100\%$ 的数据, 满足 $0 \le W_i < 10045358090$

题解

令$E = min(\lfloor \frac{N}{S} \rfloor,M)$

我们枚举有几种颜色有$K$次，那么剩余的就不能有$K$次，利用容斥我们可以得出式子：

\[ans = \sum\limits_{i = 0}^{E} w[i]{M \choose i} {N \choose iS} \frac{(iS)!}{(S!)^{i}} \sum\limits_{j = 0}^{E - i} (-1)^{j} {M - i \choose j} {N - iS \choose jS} \frac{(jS)!}{(S!)^{j}} (M - i - j)^{N - iS - jS}
\]

那个$(M - i - j)^{N - iS - jS}$非常不好处理，我们考虑转化一下：

\[ans = \sum\limits_{i = 0}^{E} w[i]{M \choose i} {N \choose iS} \frac{(iS)!}{(S!)^{i}} \sum\limits_{j = i}^{E} (-1)^{j - i} {M - i \choose j - i} {N - iS \choose jS - iS} \frac{(jS - iS)!}{(S!)^{j - i}} (M - j)^{N - jS}
\]

然后展开组合数，分子分母对消，剩余如下：

\[ans = \sum\limits_{i = 0}^{E} w[i]\frac{M!N!}{i!} \sum\limits_{j = i}^{E} \frac{(-1)^{j - i}(M - j)^{N -jS}}{(j - i)!(M - j)!(N - jS)!(S!)^{j}}
\]

我们交换一下$i,j$的位置，经整理得：

\[ans = \sum\limits_{j = 0}^{E} \frac{M!N!(M-j)^{N - jS}}{(M - j)!(N - jS)!(S!)^{j}} \sum\limits_{i = 0}^{j} \frac{w[i]}{i!} * \frac{(-1)^{j - i}}{(j - i)!}
\]

左边是只与$j$有关的式子，右边是$f(x) = \frac{w[x]}{x!}$与$g(x) = \frac{(-1)^{x}}{x!}$的卷积

NTT即可

$1004535809$的原根是$3$

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 100005,maxm = 10000005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
const int G = 3,P = 1004535809;
int qpow(int a,int b){
	int ans = 1;
	for (; b; b >>= 1,a = 1ll * a * a % P)
		if (b & 1) ans = 1ll * ans * a % P;
	return ans;
}
int fac[maxm],fv[maxm],inv[maxm];
int L,R[maxn << 2],f[maxn << 2],g[maxn << 2],n,m;
int N,M,S,W[maxn];
void NTT(int* a,int F){
	for (int i = 0; i < n; i++) if (i < R[i]) swap(a[i],a[R[i]]);
	for (int i = 1; i < n; i <<= 1){
		int gn = qpow(G,(P - 1) / (i << 1));
		for (int j = 0; j < n; j += (i << 1)){
			LL g = 1,x,y;
			for (int k = 0; k < i; k++,g = 1ll * g * gn % P){
				x = a[j + k]; y = 1ll * g * a[j + k + i] % P;
				a[j + k] = (x + y) % P; a[j + k + i] = (x - y + P) % P;
			}
		}
	}
	if (F == 1) return;
	int nv = qpow(n,P - 2); reverse(a + 1,a + n);
	for (int i = 0; i < n; i++) a[i] = 1ll * a[i] * nv % P;
}
void init(){
	int E = max(N,M);
	fac[0] = 1;
	for (int i = 1; i <= E; i++) fac[i] = 1ll * fac[i - 1] * i % P;
	inv[0] = inv[1] = 1;
	for (int i = 2; i <= E; i++) inv[i] = 1ll * (P - P / i) * inv[P % i] % P;
	fv[0] = 1;
	for (int i = 1; i <= E; i++) fv[i] = 1ll * fv[i - 1] * inv[i] % P;
}
void solve(){
	int t,E = min(M,N / S);
	for (int i = 0; i <= E; i++){
		t = (i & 1) ? -1 : 1;
		f[i] = 1ll * W[i] * fv[i] % P;
		g[i] = 1ll * t * fv[i] % P;
	}
	L = 0; m = E + E;
	for (n = 1; n <= m; n <<= 1) L++;
	for (int i = 1; i < n; i++) R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
	NTT(f,1); NTT(g,1);
	for (int i = 0; i < n; i++) f[i] = 1ll * f[i] * g[i] % P;
	NTT(f,-1);
	int ans = 0,tmp;
	for (int i = 0; i <= E; i++){
		tmp = 1ll * fac[M] * fac[N] % P * qpow(M - i,N - i * S) % P;
		tmp = 1ll * tmp * fv[N - i * S] % P * fv[M - i] % P * qpow(fv[S],i) % P;
		ans = (ans + 1ll * tmp * f[i] % P) % P;
	}
	printf("%d\n",(ans % P + P) % P);
}
int main(){
	N = read(); M = read(); S = read();
	for (int i = 0; i <= M; i++) W[i] = read();
	init();
	solve();
	return 0;
}