HDU3723 Delta Wave —— 卡特兰数

题目链接：https://vjudge.net/problem/HDU-3723

Delta Wave

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1468    Accepted Submission(s): 483

Problem Description

A delta wave is a high amplitude brain wave in humans with a frequency of 1 – 4 hertz which can be recorded with an electroencephalogram (EEG) and is usually associated with slow-wave sleep (SWS).
-- from Wikipedia

The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.

For example, there are the 9 kinds of delta waves for N = 4:

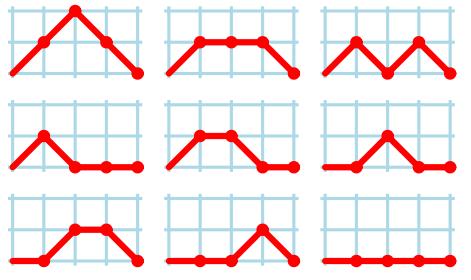
Given N, you are requested to find out how many kinds of different delta waves of otaku.

 

Input

There are no more than 20 test cases. There is only one line for each case, containing an integer N (2 < N <= 10000)

 

Output

Output one line for each test case. For the answer may be quite huge, you need only output the answer module 10¹⁰⁰.

 

Sample Input

3
4

 

Sample Output

4
9

 

Source

2010 Asia Tianjin Regional Contest

 

Recommend

zhouzeyong

题意：

从（0,0）走到（n，0）， 要求：每一步在水平方向上向右走一格，在竖直方向上可以向上走一格、向下走一个、不走。而且路线不能够穿过X轴，问：有多少种符合要求的路线？

题解：

1.可知，走多少步向上，就要多少步向下。假设有k个向上，则先选出在竖直方向上有移动的位置：C[n][2*k]

2.当选出了竖直方向有移动的位置之后，就容易得出这是一个卡特兰数。而h[k] = C[2*k][k] / (k+1)。

3. 而k的取值范围为：0~n/2，所以总共有 sigma（C[n][2*k]*C[2*k][k]/(k+1)） 0<=k<=n/2。然而，题目中n的范围为1e4，用这条计算公式，需要O(n^2)来预处理C[][]，故而超时，那怎么办？

3.1 设a[k] = C[k][2*k]*C[2*k][k]/(k+1), 则 a[k-1] = C[n][2*k-2]*C[2*k-2][k-1]/k，通过通过推导，得到：a[k] = a[k-1] * (n-2*k+1) * (n-2*k+1) / (k*(k+1)) 。这样就得出一条线性递推的式子。

3.2 所以总共有 sigma（a[k]）种情况， 0<=k<=n/2。

代码如下：

 import java.util.Scanner;
 import java.math.BigInteger;
 
 public class Main {
 
     public static void main(String[] args){
 
         BigInteger[] a = new BigInteger[10010];
         Scanner input = new Scanner(System.in);
         while(input.hasNext()){
             int n = input.nextInt();
 
             a[0] = BigInteger.ONE;
             for(int i = 1; i<=n/2; i++) {
                 a[i] = a[i-1].multiply(BigInteger.valueOf((n-2*i+1)*(n-2*i+2)));
                 a[i] = a[i].divide(BigInteger.valueOf(i*(i+1)));
             }
 
             BigInteger ans = BigInteger.ZERO;
             for(int i = 0; i<=n/2; i++) {
                 ans = ans.add(a[i]);
             }
             System.out.println(ans.mod(BigInteger.TEN.pow(100)));
         }
     }
 }