ACM学习历程—Hihocoder编程之美测试赛B题 大神与三位小伙伴（组合数学 ）

时间限制:2000ms

单点时限:1000ms

内存限制:256MB

描述

给你一个m x n (1 <= m, n <= 100)的矩阵A (0<=a_ij<=10000)，要求在矩阵中选择一些数，要求每一行，每一列都至少选到了一个数，使得选出的数的和尽量的小。

输入

多组测试数据。首先是数据组数T

对于每组测试数据，第1行是两个正整数m, n，分别表示矩阵的行数和列数。

接下来的m行，每行n个整数，之间用一个空格分隔，表示矩阵A的元素。

输出

每组数据输出一行，表示选出的数的和的最小值。

数据范围

小数据：1 <= m, n <= 5

大数据：1 <= m, n <= 100

样例输入

2
3 3
1 2 3
3 1 2
2 3 1
5 5
1 2 3 4 5
5 1 2 3 4
4 5 1 2 3
3 4 5 1 2
2 3 4 5 1

样例输出

Case 1: 3
Case 2: 5

题目大意是有三类纪念品A、B、C。每类纪念品又有N种不同的纪念品Ai、Bi、Ci（1 <= i <= N），然后对于Ai纪念品的剩余个数CAi是N+1-i个，对于Bi纪念品的剩余个数CBi是N+1-i个，Ci纪念品的剩余个数CCi是N+1-i个。

要求拿出三件纪念品Ap, Bq, Ck，不能恰好有两件价值相同，求取法数。

可以从两个角度考虑：

（1）       从正面角度考虑：

不能恰好有两件价值相同，那么就是三件价值都相同或者都不同。

1．  三件价值都相同：

假设我都取价值为i的纪念品，那么就有CAi*CBi*CCi可以取（CAi、CBi、CCi分别为Ai、Bi、Ci剩余个数）

所以总数便是

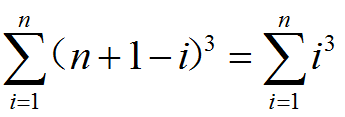
2.三件价值都不同：

假设我A取了价值为i的纪念品，那么有CAi种；

那么B不能取价值为i的，假设B取了价值为j的，有CBj种；

那么C不能取价值为i和j的。

所以总数便是

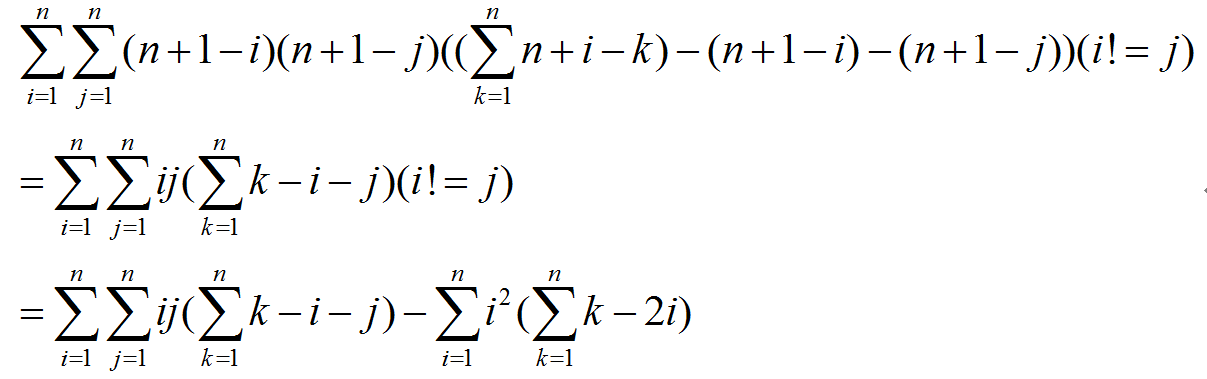
此处说明一下，第一个式子是取A乘取B乘取C（取C是在C总数的基础上减去价值为i和j的）

第二个式子就是第一个式子变形的，将n+1-i替换为i’，同理的j和k。

第三个式子就是把i != j这个条件体现出来。

接下来进一步化简：

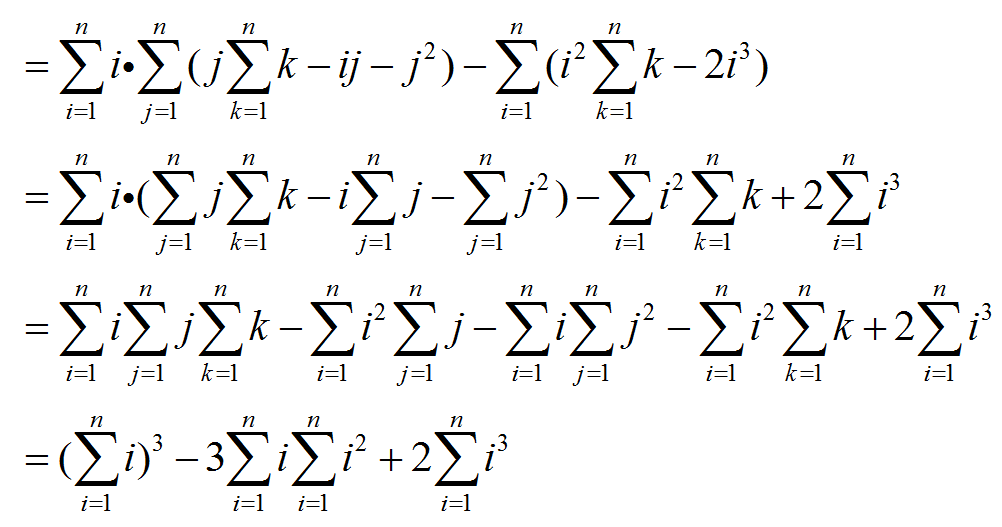
所以总的就是上面两种情况相加，得到

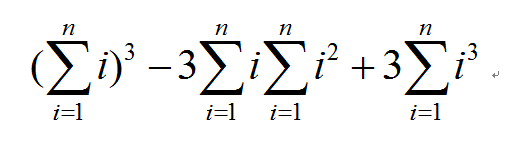
然后由下面三组式子便可以求解：

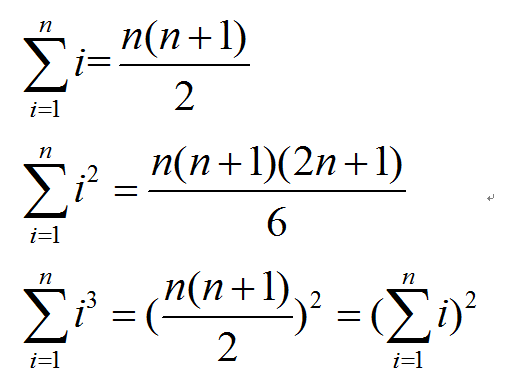
（2）       从反面角度考虑：

不能恰好有两件价值相同，那么就是总选数里面减去它就OK了。

总选数自然就是:

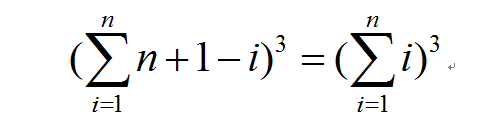
恰好有两件价值相同，那么就先从ABC三个里选出两种准备选价值相同的i，选法有C(2, 3)，即3种。

然后剩余的一个不能选价值为i的，所以总数：

所以最后答案就是：

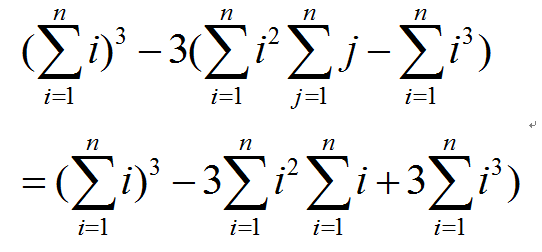
与第一种方法的答案一致。

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <string>
#define inf 0xfffffff
#define eps 1e-10
#define N 1000000007

using namespace std;

long long n, C1, C2;

void Init()
{
    n %= N;
    C1 = (n+)*n/;
    C1 %= N;
    C2 = (n+)*n/;
    if (C2% == )
    {
        C2 /= ;
        C2 %= N;
        C2 *= *n+;
        C2 %= N;
    }
    else
    {
        C2 %= N;
        C2 *= (*n+)/;
        C2 %= N;
    }
}

long long ans()
{
    long long s = (C1*C1) % N;
    s = (s*C1)%N + (*s)%N - (*((C1*C2)%N))%N;
    return (s%N+N)%N;
}

int main()
{
    //freopen("test.txt", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = ; times <= T; ++times)
    {
        scanf("%lld", &n);
        printf("Case %d: ", times);
        Init();
        printf("%lld\n", ans());
    }
    return ;
}