Kruskal与Prim

一、最小生成树

　　在无向图中，连通且不含圈的图称为树(Tree)。给定无向图G=(V,E),连接G中所有点，且边集是E的子集的树称为G的生成树(Spanning Tree),而权值最小的生成树称为最小生成树(Minning Spanning Tree,MST)。

二、Kruskal

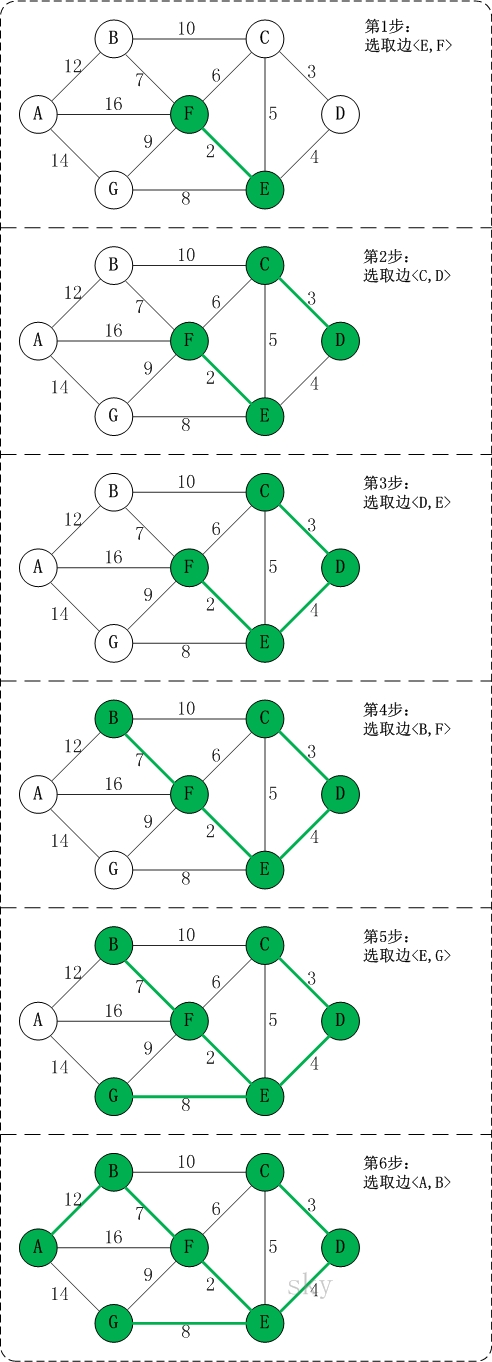
步骤：

　　1、将所有的边按照从小到大的顺序排列

　　2、从小到大一次考量每条边(u,v)，如果u和v不在同一连通分量，那么把(u,v)加入连通分量

　　3、重复步骤2，直到图中所有节点都在同一连通分量中

图解：

　　

原理：

　　如果u和v在不同的连通分量中，那么加入(u,v)一定是最优的。为什么呢？

　下面用反证法：如果这条边不在最小生成树中，它连接的两个连通分量最终还是要连起来的，通过其他的连法，那么另一种连法与这条边一定构成了环，而环中一定有一条权值大于这条边的边，用这条边将其替换掉，图仍旧保持连通，但总权值减小了。也就是说，如果不选取这条边，最后构成的生成树的总权值一定不会是最小的。

三、Prim

步骤：

　　1、初始化，V_new = {x},其中x为集合V中的任意节点(起始点)，E_new = {}

　　2、在集合E中选取权值最小的边（u, v），其中u为集合V_new中的元素，而v则是V中没有加入V_new的顶点（如果存在有多条满足                前述条件即具有相同权值的边，则可任意选取其中之一）。将v加入集合V_new中，将（u, v）加入集合E_new中；

　　3、重复操作2，直到V_new = V

图解：

　　

 证明：

　　 prim生成的树为T₀, 最小生成树（MST）为T_min

　　两棵树的边从小到大权重比较，设第一个属于 T₀ 但不属于 T_min 的边为 e_d1, 连接该边的两个顶点为 (v_s, v_e1)。同时存在第一个属          于 T_min 但不属于 T₀ 的边为 e_d2, 连接该边的两个顶点为 (v_s, v_e2)。

　　两个边的起点相同。由Prim算法性质可知，w(e_d2) >= w(e_d1)。

　　此时，在 T_min 中删除 e_d2 ，添加 e_d1，边的数量和顶点数量均不变，且不存在环，因此得到新的生成树T_new,且cost(T_min)>=cost　　　　　　        (T_new)。又因为 T_min 是MST 所以 cost(T_min)=cost(T_new)。