用“人话”解释不精确线搜索中的Armijo-Goldstein准则及Wolfe-Powell准则

转载请注明出处：http://www.codelast.com/

line search（一维搜索，或线搜索）是最优化（Optimization）算法中的一个基础步骤/算法。它可以分为精确的一维搜索以及不精确的一维搜索两大类。
在本文中，我想用“人话”解释一下不精确的一维搜索的两大准则：Armijo-Goldstein准则 ＆ Wolfe-Powell准则。
之所以这样说，是因为我读到的所有最优化的书或资料，从来没有一个可以用初学者都能理解的方式来解释这两个准则，它们要么是长篇大论、把一堆数学公式丢给你去琢磨；要么是简短省略、直接略过了解释的步骤就一句话跨越千山万水得出了结论。
每当看到这些书的时候，我脑子里就一个反应：你们就不能写人话吗？

我下面就尝试用通俗的语言来描述一下这两个准则。

【1】为什么要遵循这些准则

由于采用了不精确的一维搜索，所以，为了能让算法收敛（即：求得极小值），人们逐渐发现、证明了一些规律，当你遵循这些规律的时候，算法就很有可能收敛。因此，为了达到让算法收敛的目的，我们就要遵循这些准则。如果你不愿意遵循这些已经公认有效的准则，而是要按自己的准则来设计算法，那么恭喜你，如果你能证明你的做法是有效的，未来若干年后，书本里可能也会出现你的名字。

文章来源：http://www.codelast.com/

【2】Armijo-Goldstein准则

此准则是在196X年的时候由Armijo和Goldstein提出的，当然我没有具体去搜过这俩人是谁。在有的资料里，你可能会看到“Armijo rule”（Armijo准则）的说法，可能是同一回事，不过，任何一个对此作出重要贡献的人都是不可抹杀的，不是么？

Armijo-Goldstein准则的核心思想有两个：①目标函数值应该有足够的下降；②一维搜索的步长α不应该太小。

这两个思想的意图非常明显。由于最优化问题的目的就是寻找极小值，因此，让目标函数函数值“下降”是我们努力的方向，所以①正是想要保证这一点。

同理，②也类似：如果一维搜索的步长α太小了，那么我们的搜索类似于在原地打转，可能也是在浪费时间和精力。

文章来源：http://www.codelast.com/
有了这两个指导思想，我们来看看Armijo-Goldstein准则的数学表达式：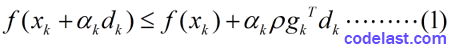

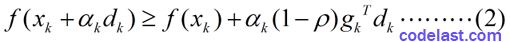
其中， 0<ρ<12 
文章来源：http://www.codelast.com/
(1)为什么要规定 ρ∈(0,12) 这个条件？其实可以证明：如果没有这个条件的话，将影响算法的超线性收敛性（定义看这个链接，第4条）。在这个速度至关重要的时代，没有超线性收敛怎么活啊！(开个玩笑)
具体的证明过程，大家可以参考袁亚湘写的《最优化理论与方法》一书，我没有仔细看，我觉得对初学者，不用去管它。
(2)第1个不等式的左边式子的泰勒展开式为：
f(xk+αkdk)=f(xk)+αkgkTdk+o(αk) 
去掉高阶无穷小，剩下的部分为： f(xk)+αkgkTdk 
而第一个不等式右边与之只差一个系数 ρ 
我们已知了 gkTdk<0 （这是 dk 为下降方向的充要条件），并且 ρ∈(0,12) ，因此，1式右边仍然是一个比 f(xk) 小的数，即：
f(xk)+αkρgkTdk<f(xk) 
也就是说函数值是下降的（下降是最优化的目标）。
文章来源：http://www.codelast.com/
(3)由于 ρ∈(0,12) 且 gkTdk<0 （ dk 是一个下降方向的充要条件），故第2个式子右边比第1个式子右边要小，即：
αk(1−ρ)gkTdk<αkρgkTdk<0 
如果步长 α 太小的话，会导致这个不等式接近于不成立的边缘。因此，式2就保证了 α 不能太小。
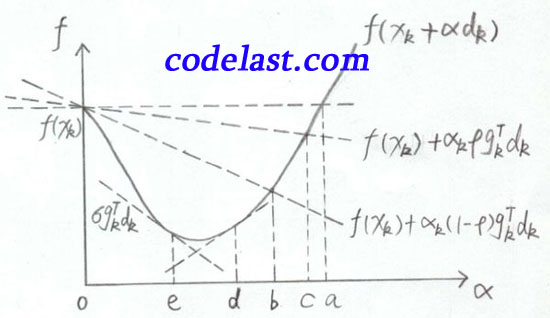
(4)我还要把很多书中都用来描述Armijo-Goldstein准则的一幅图搬出来说明一下（亲自手绘）：

文章来源：http://www.codelast.com/
横坐标是 α ，纵坐标是 f ，表示在 xk,dk 均为常量、 α 为自变量变化的情况下，目标函数值随之变化的情况。
之所以说 xk,dk 均为常量，是因为在一维搜索中，在某一个确定的点 xk 上，搜索方向 dk 确定后，我们只需要找到一个合适的步长 α 就可以了。
当 x 为常量， α 为自变量时， f(x+αd) 可能是非线性函数（例如目标函数为 y=x2 时）。因此图中是一条曲线。
右上角的 f(xk+αdk) 并不是表示一个特定点的值，而是表示这条曲线是以 α 为自变量、 xk,dk 为常量的函数图形。
当 α=0 时，函数值为 f(xk) ，如图中左上方所示。水平的那条虚线是函数值为 f(xk) 的基线，用于与其他函数值对比。
f(xk)+αkρgkTdk 那条线在 f(xk) 下方（前面已经分析过了，因为 gkTdk<0 ）， f(xk)+αk(1−ρ)gkTdk 又在 f(xk)+αkρgkTdk 的下方（前面也已经分析过了），所以Armijo-Goldstein准则可能会把极小值点（可接受的区间）判断在区间bc内。显而易见，区间bc是有可能把极小值排除在外的（极小值在区间ed内）。
所以，为了解决这个问题，Wolfe-Powell准则应运而生。
文章来源：http://www.codelast.com/
【3】Wolfe-Powell准则
在某些书中，你会看到“Wolfe conditions”的说法，应该和Wolfe-Powell准则是一回事——可怜的Powell大神又被无情地忽略了...
Wolfe-Powell准则也有两个数学表达式，其中，第一个表达式与Armijo-Goldstein准则的第1个式子相同，第二个表达式为：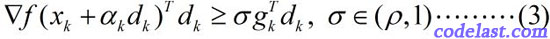

这个式子已经不是关于函数值的了，而是关于梯度的。
此式的几何解释为：可接受点处的切线斜率≥初始斜率的 σ 倍。
上面的图已经标出了 σgTkdk 那条线（即 e 点处的切线），而初始点（ α=0 的点）处的切线是比 e 点处的切线要“斜”的，由于 σ∈(ρ,1) ，使得 e 点处的切线变得“不那么斜”了——不知道这种极为通俗而不够严谨的说法，是否有助于你理解。
这样做的结果就是，我们将极小值包含在了可接受的区间内（ e 点右边的区间）。
文章来源：http://www.codelast.com/
Wolfe-Powell准则到这里还没有结束！在某些书中，你会看到用另一个所谓的“更强的条件”来代替(3)式，即：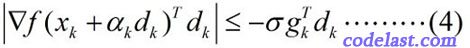

这个式子和(3)式相比，就是左边加了一个绝对值符号，右边换了一下正负号（因为 gTkdk<0 ，所以 −σgTkdk>0 ）。
这样做的结果就是：可接受的区间被限制在了 [b,d] 内，如图：

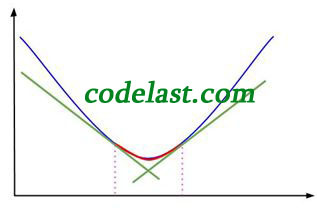
图中红线即为极小值被“夹击”的生动演示。