Machine Learning 算法可视化实现1 - 线性回归

一、原理和概念

1.回归

回归最简单的定义是，给出一个点集D，用一个函数去拟合这个点集。而且使得点集与拟合函数间的误差最小，假设这个函数曲线是一条直线，那就被称为线性回归；假设曲线是一条二次曲线，就被称为二次回归。

以下仅介绍线性回归的基本实现。

2.假设函数、误差、代价函数

参考  Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)

最小化误差一般有两个方法：最小二乘法和梯度下降法

最小二乘法可以一步到位，直接算出未知参数，但他是有前提的。梯度下降法和最小二乘法不一样，它通过一步一步的迭代，慢慢的去靠近到那条最优直线。

平方误差：

代价函数：

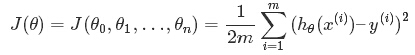（系数是为了之后求梯度的时候方便）

3.梯度下降算法

梯度下降算法是一种优化算法，它可以帮助我们找到一个函数的局部极小值，不仅用在线性回归模型中，非线性也可以。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

下图是假设函数 h(x)、 代价函数J()和梯度下降算法：

完整的梯度下降算法：

梯度下降算法的Python实现：

# -*- coding: utf-8 -*-
# @Time    : 2018/3/6 18:32
# @Author  : TanRong
# @Software: PyCharm
# @File    : gradient descent.py

import numpy as np
import matplotlib.pyplot
import pylab

# 参数含义：y=kx+b；learning_rate学习速率、步长幅度；num_iter迭代的次数

#计算梯度并更新k，b
def gradient(current_k, current_b, data, learning_rate):
    k_gradient = 0
    b_gradient = 0
    m = float(len(data))
    for i in range(0, len(data)):
        x = data[i,0]
        y = data[i,1]
        k_gradient += (1/m)*(current_k*x + current_b - y) * x
        b_gradient += (1/m)*(current_k*x + current_b - y)
    update_k = current_k - learning_rate * k_gradient
    update_b = current_b - learning_rate * b_gradient
    return[update_k, update_b]

#优化器
def optimizer(data, initial_k, initial_b, learning_rate, num_iter):
    k = initial_k
    b = initial_b

    #Gradient descent 梯度下降
    for i in range(num_iter):
        #更新 k、b
        k,b = gradient(k, b, data, learning_rate)
    return [k,b]

#绘图
def plot_data(data, k, b):
    x = data[:,0]
    y = data[:,1]
    y_predict = k * x + b
    pylab.plot(x,y,'o')
    pylab.plot(x,y_predict,'k-')
    pylab.show()

#计算平方差
def error(data, k, b):
    totalError = 0;
    for i in range(0, len(data)):
        x = data[i,0]
        y = data[i,1]
        totalError += (k*x+b-y)**2
        return totalError / float(len(data))
#梯度下降算法 实现线性回归
def Linear_regression():
    data = np.loadtxt('train_data.csv', delimiter = ',')  #训练数据
    learning_rate = 0.01
    initial_k = 0.0
    initial_b = 0.0
    num_iter = 1000

    [k,b] = optimizer(data, initial_k, initial_b, learning_rate, num_iter)
    print("k:", k,";b:", b)
    print("平方差/代价函数：", error(data, k, b))

    plot_data(data, k, b)

Linear_regression()

代码和数据的下载：https://github.com/~~~

（数据用的别人的）

参考代码：

#http://blog.csdn.net/sxf1061926959/article/details/66976356?locationNum=9&fps=1

import numpy as np
import pylab

def compute_error(b,m,data):

    totalError = 0
    #Two ways to implement this
    #first way
    # for i in range(0,len(data)):
    #     x = data[i,0]
    #     y = data[i,1]
    #
    #     totalError += (y-(m*x+b))**2

    #second way
    x = data[:,0]
    y = data[:,1]
    totalError = (y-m*x-b)**2
    totalError = np.sum(totalError,axis=0)

    return totalError/float(len(data))

def optimizer(data,starting_b,starting_m,learning_rate,num_iter):
    b = starting_b
    m = starting_m

    #gradient descent
    for i in range(num_iter):
        #update b and m with the new more accurate b and m by performing
        # thie gradient step
        b,m =compute_gradient(b,m,data,learning_rate)
        if i%100==0:
            print 'iter {0}:error={1}'.format(i,compute_error(b,m,data))
    return [b,m]

def compute_gradient(b_current,m_current,data ,learning_rate):

    b_gradient = 0
    m_gradient = 0

    N = float(len(data))
    #Two ways to implement this
    #first way
    # for i in range(0,len(data)):
    #     x = data[i,0]
    #     y = data[i,1]
    #
    #     #computing partial derivations of our error function
    #     #b_gradient = -(2/N)*sum((y-(m*x+b))^2)
    #     #m_gradient = -(2/N)*sum(x*(y-(m*x+b))^2)
    #     b_gradient += -(2/N)*(y-((m_current*x)+b_current))
    #     m_gradient += -(2/N) * x * (y-((m_current*x)+b_current))

    #Vectorization implementation
    x = data[:,0]
    y = data[:,1]
    b_gradient = -(2/N)*(y-m_current*x-b_current)
    b_gradient = np.sum(b_gradient,axis=0)
    m_gradient = -(2/N)*x*(y-m_current*x-b_current)
    m_gradient = np.sum(m_gradient,axis=0)
        #update our b and m values using out partial derivations

    new_b = b_current - (learning_rate * b_gradient)
    new_m = m_current - (learning_rate * m_gradient)
    return [new_b,new_m]

def plot_data(data,b,m):

    #plottting
    x = data[:,0]
    y = data[:,1]
    y_predict = m*x+b
    pylab.plot(x,y,'o')
    pylab.plot(x,y_predict,'k-')
    pylab.show()

def Linear_regression():
    # get train data
    data =np.loadtxt('data.csv',delimiter=',')

    #define hyperparamters
    #learning_rate is used for update gradient
    #defint the number that will iteration
    # define  y =mx+b
    learning_rate = 0.001
    initial_b =0.0
    initial_m = 0.0
    num_iter = 1000

    #train model
    #print b m error
    print 'initial variables:\n initial_b = {0}\n intial_m = {1}\n error of begin = {2} \n'\
        .format(initial_b,initial_m,compute_error(initial_b,initial_m,data))

    #optimizing b and m
    [b ,m] = optimizer(data,initial_b,initial_m,learning_rate,num_iter)

    #print final b m error
    print 'final formula parmaters:\n b = {1}\n m={2}\n error of end = {3} \n'.format(num_iter,b,m,compute_error(b,m,data))

    #plot result
    plot_data(data,b,m)

if __name__ =='__main__':

    Linear_regression()

有一些其他方法实现某个功能，可以再看一遍

参考链接：https://www.cnblogs.com/yangykaifa/p/7261316.html

http://blog.csdn.net/sxf1061926959/article/details/66976356?locationNum=9&fps=1