UVA12569-Planning mobile robot on Tree (EASY Version)（BFS+状态压缩）

Problem UVA12569-Planning mobile robot on Tree (EASY Version)

Accept：138  Submit：686

Time Limit: 3000 mSec

 Problem Description

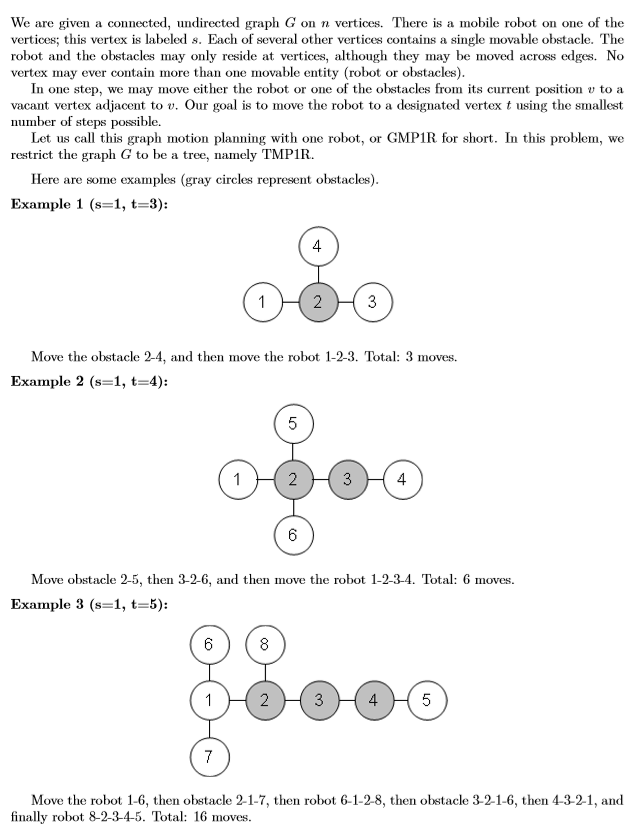
 Input

The first line contains the number of test cases T (T ≤ 340). Each test case begins with four integers n, m, s, t (4 ≤ n ≤ 15, 0 ≤ m ≤ n−2, 1 ≤ s,t ≤ n, s ̸= t), the number of vertices, the number of obstacles and the label of the source and target. Vertices are numbered 1 to n. The next line contains m different integers not equal to s, the vertices containing obstacles. Each of the next n − 1 lines contains two integers u and v (1 ≤ u < v ≤ n), that means there is an edge u−v in the tree.

 Output

For each test case, print the minimum number of moves k in the first line. Each of the next k lines containstwointegers a and b,thatmeanstomovetherobot/obstaclefrom a to b. Ifthereisnosolution, print ‘-1’. If there are multiple solutions, any will do. Print a blank line after each test case.

 Sample Input

3
4 1 1 3
2
1 2
2 3
2 4
6 2 1 4
2 3
1 2
2 3
3 4
2 5
2 6
8 3 1 5
2 3 4
1 2
2 3
3 4
4 5
1 6
1 7
2 8

 

 Sample Ouput

Case 1: 3
2 4
1 2
2 3

Case 2: 6
2 6
3 2
2 5
1 2
2 3
3 4

Case 3: 16
1 7
2 1
1 6
7 1
1 2
2 8
3 2
2 1
1 7
4 3
3 2
2 1
8 2
2 3
3 4
4 5

 

题解：看到n的范围状压是比较正的思路，二进制储存，BFS搜索，vis数组稍微有一点改动，其中一维记录石头，再有一维记录机器人。水题。

 

 #include <bits/stdc++.h>
 
 using namespace std;
 
 const int maxn = ;
 int n, m, s, t;
 int ori;
 
 struct Edge {
     int to, next;
 }edge[maxn << ];
 
 struct Node {
     int sit, robot;
     int time;
     Node(int sit = , int robot = , int time = ) :
         sit(sit), robot(robot), time(time) {}
 };
 
 int tot, head[maxn];
 pair<int,int> pre[][maxn];
 bool vis[][maxn];
 
 void init() {
     tot = ;
     memset(head, -, sizeof(head));
     memset(pre, -, sizeof(pre));
     memset(vis, false, sizeof(vis));
 }
 
 void AddEdge(int u, int v) {
     edge[tot].to = v;
     edge[tot].next = head[u];
     head[u] = tot++;
 }
 
 inline int get_pos(int x) {
     return  << x;
 }
 
 int bfs(pair<int,int> &res) {
     queue<Node> que;
     que.push(Node(ori, s, ));
     vis[ori][s] = true;
 
     while (!que.empty()) {
         Node first = que.front();
         que.pop();
         if (first.robot == t) {
             res.first = first.sit, res.second = first.robot;
             return first.time;
         }
         int ssit = first.sit, rrob = first.robot;
         //printf("%d %d\n", ssit, rrob);
 
         for (int i = head[rrob]; i != -; i = edge[i].next) {
             int v = edge[i].to;
             if (ssit&get_pos(v) || vis[ssit][v]) continue;
             vis[ssit][v] = true;
             que.push(Node(ssit, v, first.time + ));
             pre[ssit][v] = make_pair(ssit, rrob);
         }
 
         for (int i = ; i < n; i++) {
             if (ssit&(get_pos(i))) {
                 for (int j = head[i]; j != -; j = edge[j].next) {
                     int v = edge[j].to;
                     if (v == rrob || (ssit & get_pos(v))) continue;
                     int tmp = ssit ^ get_pos(v);
                     tmp ^= get_pos(i);
                     if (vis[tmp][rrob]) continue;
                     vis[tmp][rrob] = true;
                     que.push(Node(tmp, rrob, first.time + ));
                     pre[tmp][rrob] = make_pair(ssit, rrob);
                 }
             }
         }
     }
     return -;
 }
 
 void output(pair<int,int> a) {
     if (a.first == ori && a.second == s) return;
     output(pre[a.first][a.second]);
     int ppre = pre[a.first][a.second].first, now = a.first;
 
     if (ppre^now) {
         int b = -, c = -;
         for (int i = ; i < n; i++) {
             if (((ppre & ( << i)) == ( << i)) && ((now & ( << i)) == )) {
                 b = i;
             }
             else if (((ppre & ( << i)) == ) && ((now & ( << i)) == ( << i))) {
                 c = i;
             }
         }
         printf("%d %d\n", b + , c + );
     }
     else {
         printf("%d %d\n", pre[a.first][a.second].second + , a.second + );
     }
 }
 
 int con = ;
 
 int main()
 {
     int iCase;
     scanf("%d", &iCase);
     while (iCase--) {
         init();
         scanf("%d%d%d%d", &n, &m, &s, &t);
         s--, t--;
         ori = ;
         int x;
         for (int i = ; i <= m; i++) {
             scanf("%d", &x);
             x--;
             ori ^= get_pos(x);
         }
 
         int u, v;
         for (int i = ; i <= n - ; i++) {
             scanf("%d%d", &u, &v);
             u--, v--;
             AddEdge(u, v);
             AddEdge(v, u);
         }
 
         pair<int, int> res;
         int ans = bfs(res);
         printf("Case %d: %d\n", con++, ans);
         if (ans != -) output(res);
         printf("\n");
     }
     return ;
 }