[matlab] 12.Optimization Tool的使用

1.quadprog 二次规划的函数

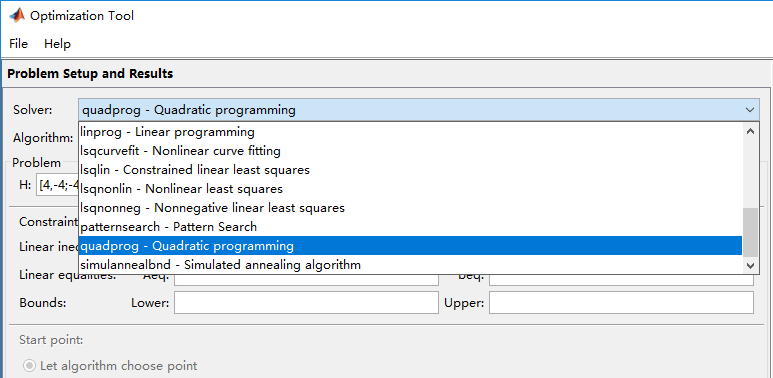
Matlab 中二次规划的数学模型可表述如下

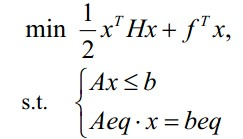
其中

H是把目标函数二次项部分进行实对称矩阵，

f是线性函数的列向量。

例求解二次规划

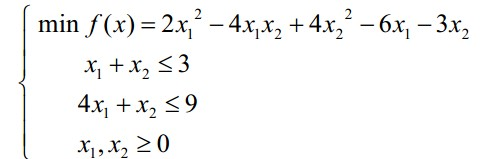
得到

h=[4,-4;-4,8]; 注意Matlab 中二次规划的数学模型中H 之前有个1/2 所以 对称二次型矩阵要乘以2 即2.*[2,-2;-2,4]=[4,-4;-4,8]

f=[-6;-3]; 目标函数线性部分的列向量。

a=[1,1;4,1]; 不等式约束的A矩阵

b=[3;9]; 

lower[0,0]

依次输入Optimization Tool

2.单一目标ga求解 遗传算法  (可以替代1中的解法,比较万能 不过求出来的是近似最优解)

第一步首先是编写适应度函数 fitness.m

function f =fitness(x)
f1=4*x(1).^3+4*x(1)*x(2)+2*x(2).^2-42*x(1)-14;
f2=4*x(2).^3+4*x(1)*x(2)+2*x(2).^2-26*x(1)-22;
f=f1.^2+f2.^2;

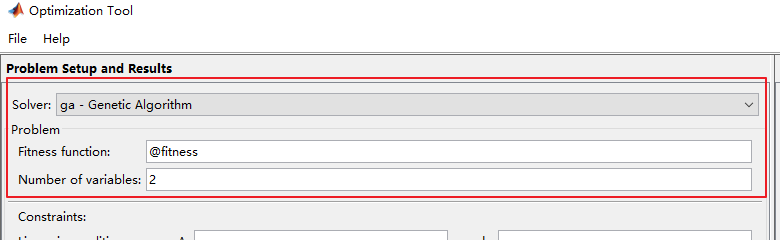
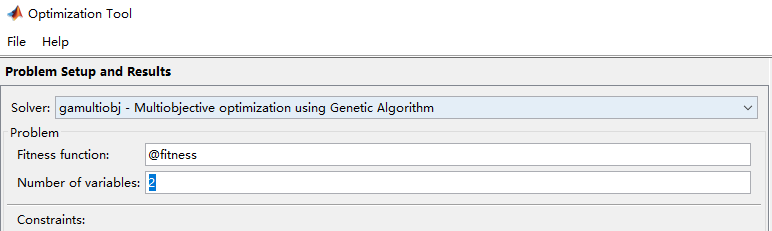
Fitness function 填写适应度函数的句柄

有两个变量 所以填2

然后勾选右边option进行具体参数调整,最后勾选绘图

得到结果

最终值 x1=-0.275 x2=1.448 fval=0.0165

3.多目标优化 gamultiobj

function f =fitness(x)
f(1)=x(1)^4-10*x(1)^2+x(1)*x(2)+x(2)^4-(x(1)^2)*(x(2)^2);
f(2)=x(2)^4-(x(1)^2)*(x(2)^2)+x(1)^4+x(1)*x(2);

多目标适应度函数 fitness.m

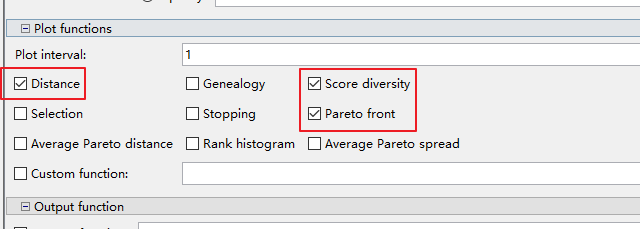
这三个绘图选项 勾选 特别是Pareto front

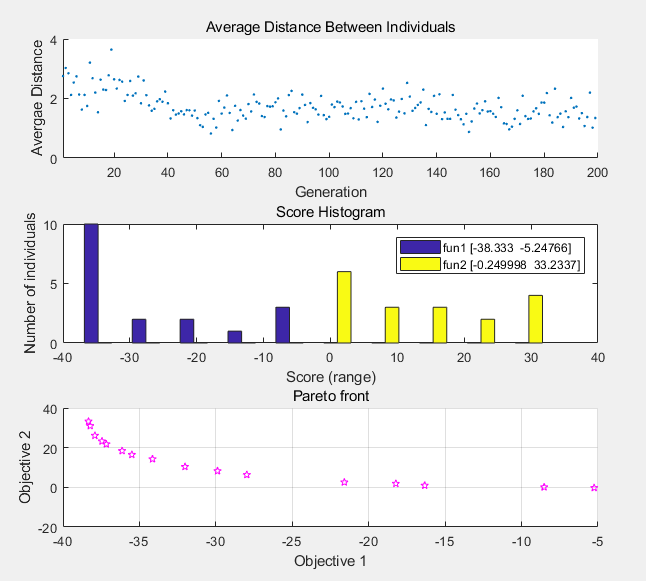
最后得到结果 x1,x2,f1,f2

4.模拟退火算法SA 工具箱应用

function y = fitness(x)
y = 20+x(1)^2+x(2)^2-10*(cos(2*pi*x(1))+cos(2*pi*x(2)));

求最小值

x0=[2.5,2.5] %初始值

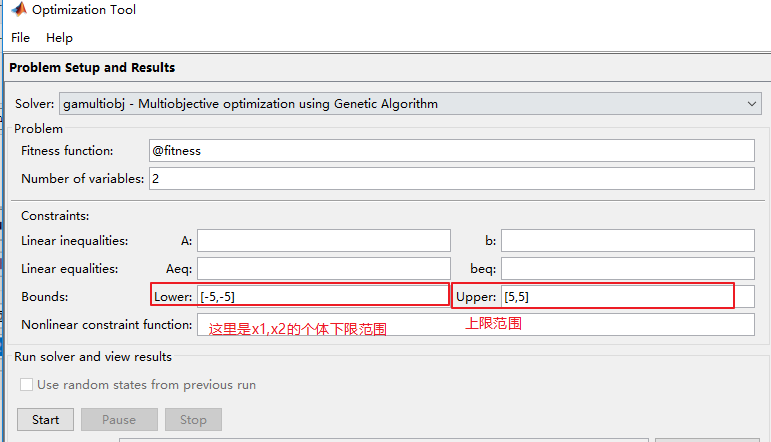
lb=[-5,-5]变量下界

ub=[5,5]变量上届

右边参数 function tolerance 改成1e-10 精度更大

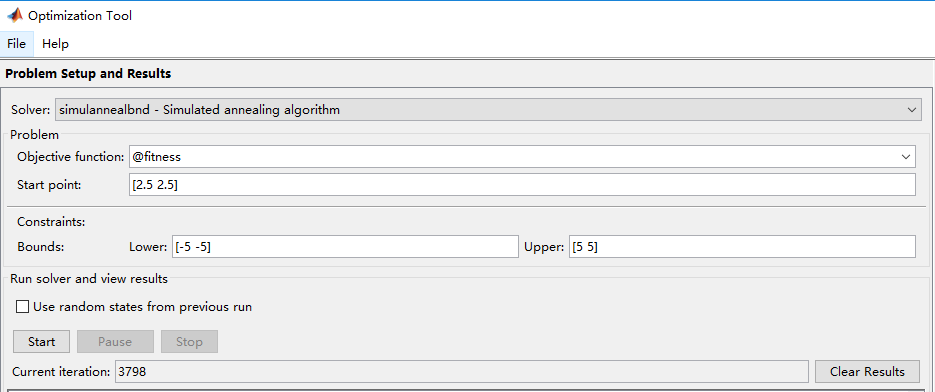
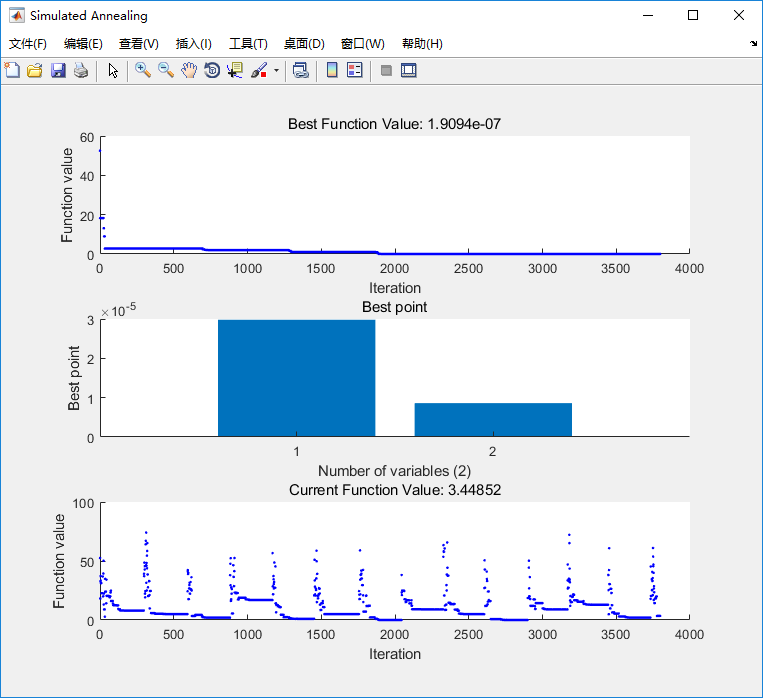
得到最优结果 x1=0 ,x2=0 y=0

5.fsolve 用最小二乘法来求解非线性方程组

function q= fitness(p)
x=p(1);
y=p(2);
q(1)=x-0.6*sin(x)-0.3*cos(y);
q(2)=y-0.6*cos(x)+0.3*sin(y);

fitness.m

P为输入的2*1矩阵[x y] 通常输入初始点

在给定的初值x0=0.5,y0=0.5下，调用fsolve函数求方程的根。