AlphaGo原理浅析

一、PolicyNetwork（走棋网络）

首先来讲一下走棋网络。我们都知道，围棋的棋盘上有19条纵横交错的线总共构成361个交叉点，状态空间非常大，是不可能用暴力穷举的方式来模拟下棋的。但是我们可以换一种思路，就是让计算机来模拟职业棋手来下棋。DeepMind团队首先想到的是用深度卷积神经网络，即DCNN来学习职业棋手下棋。他们将围棋棋盘上的盘面视为19*19的图片作为输入，黑子标为1，白子标为-1，无子标为0。但是还不能仅仅将这一张图送入网络中进行训练，因为围棋盘面的情况非常复杂，棋子之间的关系都是非线性的，所以如果只输入这一个矩阵的话训练起来会很耗资源和计算量。

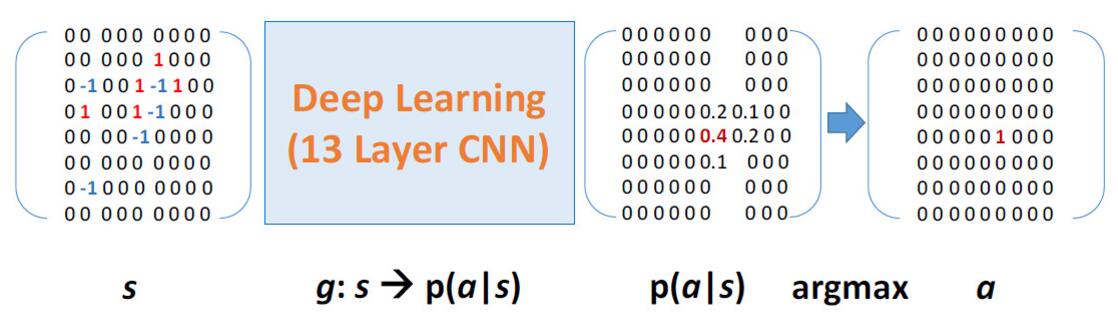
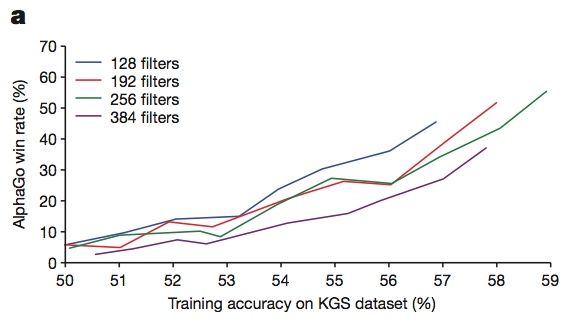
所以DeepMind团队又把一些新的特征维度送到深度卷积神经网络中，让模型训练变得更加简单，这些新的特征由围棋术语中的气、目、空这些概念构成。最终他们将棋盘局面变成48张图，也就是最终输入深度卷积神经网络中的是一个19*19*48的图像栈，将输入代入到13层的卷积神经网络中进行训练，选择192个滤波器进行卷积，最终输出一个361维的向量,表示的是职业棋手在棋盘上每个交叉点上落子的概率，比如这幅图中输出的是职业棋手大概率在这个范围内落子，然后在这个点落子的概率是0.4，所以计算机就会选择在概率最高的这个0.4的点落子。这套网络的训练集是16万局6-9段的人类职业棋手的对弈棋谱，收取了将近3000万步。最终这套网络经过训练之后已经能正确符合57%的人类落子行为，已经能和业余水平的人类棋手过招。这张图显示了策略网络的战力相对于训练后准确性的关系，可以看到当网络的卷积核个数为384个时，这个走棋网络具有最高的水平，但是为了兼顾速度他们最终选择卷积核个数为192个。

这张图列出的是他们最终选择的作为每个棋局输入的48个特征面。

二、Fastrollout（快速走子）

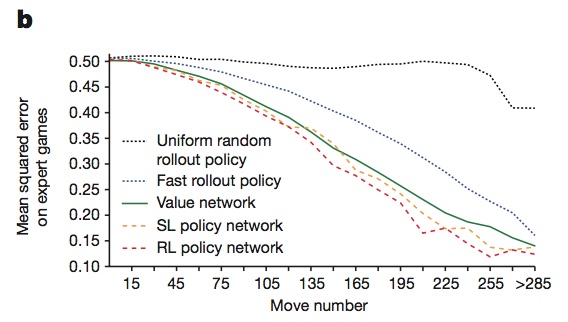
我们得到的这个走棋网络效果还算不错，但是运行速度太慢了，要用3毫秒，而围棋是一项需要计时的比赛，也就是说速度越快，那么也就代表着AlphaGo具有越高的下棋水平，所以DeepMind又做了一个相对简化的版本，叫作快速走子。快速走子用的是局部特征匹配加线性回归的方法，比使用神经网络的走棋网络快了1000倍，但是模拟职业棋手的准确率降低了一半。这张图显示了采用不同的策略进行下棋的准确性的比较，可以看到快速走子和前面所提到的走棋网络还是有一定差距的。

三、ValueNetwork（估值网络）

现在我们已经有了一个比较强但是很慢的监督学习走棋网络，以及一个很快但是准确率相对较低的快速走子网络，这两个网络一起构成了AlphaGo的落子选择器，即告诉AlphaGo下一步可以走哪些步。但仅有策略网络的AlphaGo还不够强，因为它只是模拟人类棋手下棋，学习的是人类棋手的方法，那16万局的棋谱也不都是顶尖人类棋手的棋谱，好棋坏棋它都有学，所以仅靠策略网络永远也无法达到顶尖的水平。于是DeepMInd团队又加入了一个估值网络，用来表示某一局面下双方的输赢概率。训练一个这样的网络肯定需要数据集，注意这时候他们就运用了增强学习的方法。我们前面说的，用16万张棋谱训练出了一个走棋网络P_σ1，然后再用P_σ1与P_σ1左右互搏模拟对弈比如1万局，得到1万局新的棋谱。之后再用新的棋谱训练出P_σ2。再用P_σ2与P_σ2左右互搏得到P_σ3，以此类推最终得到P_σn。我们将P_σn取一个新名字叫做Pρ，即增强学习的策略网络（RL）。这时的Pρ与最原始的P_σ1对局可以达到80%的胜率，但是Pρ与人类棋手的比赛却效果反而不如P_σ1，这可能是因为Pρ的落子选择过于单一，而人类棋手非常狡猾，下棋的时候套路很多，所以实战效果很差。但是我们用增强学习方法得到了很多质量很好的样本用于估值网络v(s)来训练，实验表明基于Pρ训练的估值网络的效果要好于最原始的P_σ1。

四、蒙特卡洛树搜索算法

现在我们有一快一慢的两个策略网络以及一个估计局面输赢的估值网络。我们可以先用策略网络模拟人类棋手走子，它得到了一个人类棋手常见的走棋范围，把整个棋面的361个落子点压缩到一个比较小的范围，减少了需要考虑的可能性。之后再用基于增强学习训练出来的估值网络筛选出赢棋概率较高的落子方案。但是高手下棋的时候都是“手下一着子，心想三步棋”，实际甚至都不止想三步之后的情况。比如实际情况往往是这一手你下了a₁，你的胜率是70%，轮到对方下一手a₂，对方的赢棋概率是60%，而第三步轮到你下a₃的时候你的赢棋概率降到了30%，那么你当初要不要下a₁这一手呢？为什么三步之后我们的赢棋概率从70%降到了30%呢？因为我们的估值函数v(s)模拟的是我们通过增强学习的下棋策略下完全局所得到的胜率，但是实战中人类棋手有一定概率不按照的套路来下，所以估值函数会出现误差，导致下着下着AlphaGo的胜率变低了。所以我们前面得到的估值函数，也就是这里vaule network还不太完美，这里我们就要引入蒙特卡洛树搜索（MCTS）的概念，将走棋网络、快速走子以及估值网络结合到这个框架上来。

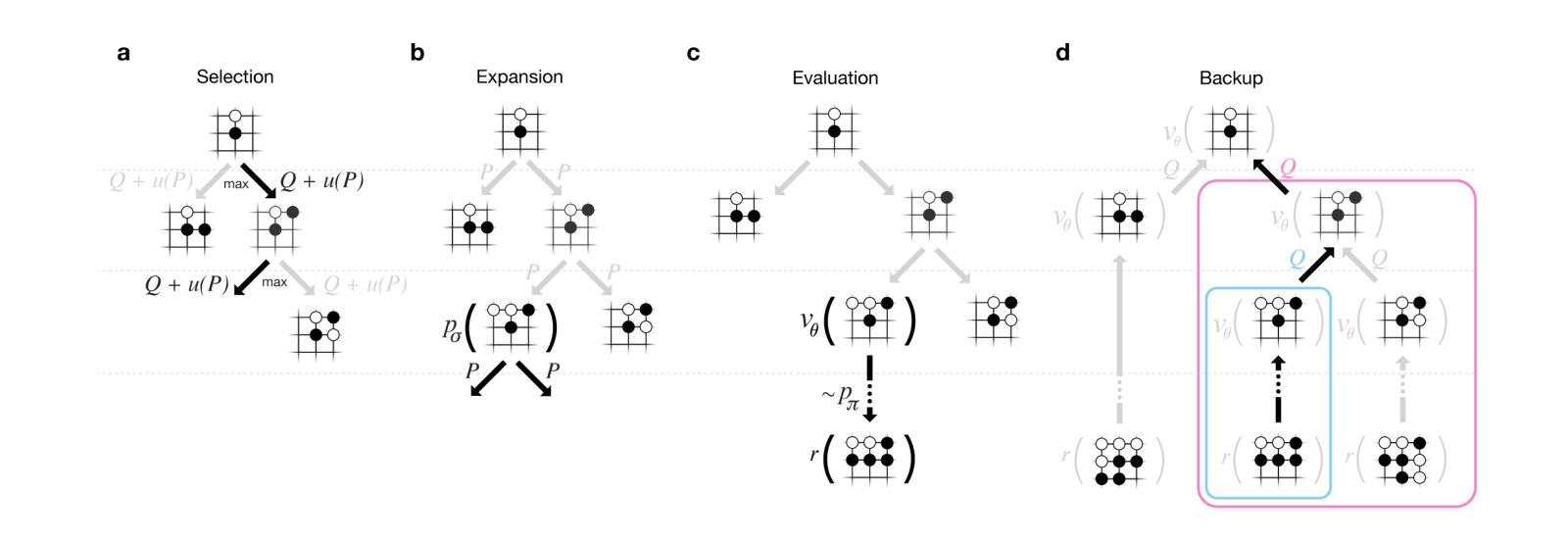
具体的方法就是，首先用得到一个棋局，先用走棋网络开局，走L步，选取比较有价值的走法得到一颗树，给每个走法一个初始的分数。先选择初始分数最高的a点，在a点上用蒙特卡洛搜索树的架构调用快速走子网络，将L步之后的棋局模拟到底，并模拟出多盘未来的对局，最终得到一个估值分数z。并在此同时在这个a点调用我们前面提到的估值网络v(s)，那么a点的新分数=调整后的初始分+ 0.5 通过模拟得到的赢棋概率 + 0.5 局面评估分。之后再更新a点上级所有根节点的分数，更新的方法就是把所有子节点的分数相加取平均值。这样再选取一个更新后的最高的分数进行模拟，一直不断地模拟和更新分数，直到最后选取一个访问次数最多的节点，而不是最终分数最高的节点，因为访问次数最多的节点比分数最高的节点要更加可靠。这样我们就完成了AlphaGo对某一局面的决策，选择蒙特卡洛树中访问次数最多的节点作为下一步的走法，最终取得了非常好的效果。

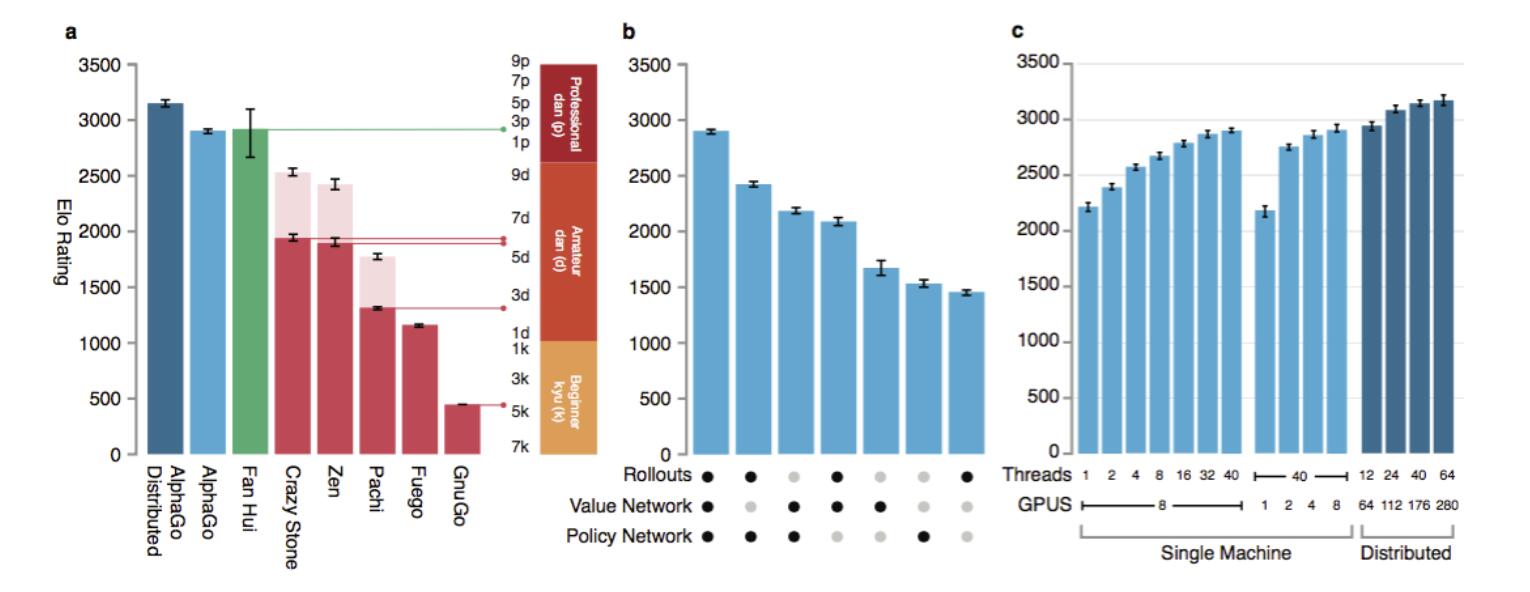
a是DeepMind团队后面将不同围棋程序之间比赛所得到的结果图，每个程序在走子之前大约有5秒的计算时间。为了让AlphaGo面对的比赛更富有挑战性，一些程序在和其他对手比赛时被让了4子。程序水平的评估基于Elo尺度：一个230点的差距大概相对于79%的赢率，大概相应于KGS的一个业余段级之间的差距。和人类欧洲冠军樊麾的比赛也包含在图上，但这些比赛使用更长的赛时制。此图所示的置信区间为95%。b是使用不同部件进行组合的单机版本的AlphaGo的表现。只单单使用策略网络则意味着没有任何搜索。c是AlphaGo的蒙特卡洛树搜索的搜索县城和GPU的可扩展性研究，使用异步（浅蓝）或分布式（深蓝）搜索，每次走子有2秒的计算时间。

后记：

以上都是我在看过论文原文以及一些大牛写的AlphaGo原理的博客后自己的一些理解，其中有很多细节方面并没有涉及到，如有错误望大家能批评指正。

参考文献：

1、AlphaGo原理解析

2、28 天自制你的 AlphaGo（五）：蒙特卡洛树搜索（MCTS）基础

3、论文笔记：Mastering the game of Go with deep neural networks and tree search (AlphaGo)

4、AlphaGo的分析

5、机器学习系列(8)_读《Nature》论文，看AlphaGo养成