绘制ROC曲线
什么是ROC曲线
ROC曲线是什么意思,书面表述为:
“ROC 曲线(接收者操作特征曲线)是一种显示分类模型在所有分类阈值下的效果的图表。”
好吧,这很不直观。其实就是一个二维曲线,横轴是FPR,纵轴是TPR:
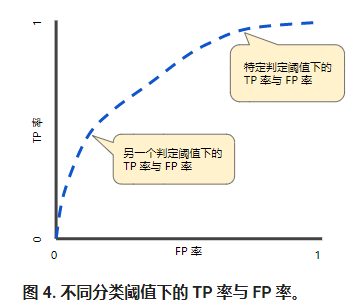
至于TPR,FPR怎么计算:
首先要明确,我们是在讨论分类问题中,讨论怎样绘制ROC曲线的,大前提是分类问题。别想太多,就当是二分类问题好了,一类是Positive,一类是Negative
分类模型的预测结果,被阈值化之后,判定为TP,FP,TN,FN四种情况:
- if Y_pred ≥ thresh and Y_gt is Positive, then TP++
- if Y_pred ≥ thresh and Y_gt is Negative, then FP++
- if Y_pred < thresh and Y_gt is Positive, then FN++
- if Y_pred < thresh and Y_gt is Negative, then TN++
然后TPR, FPR的定义为
TPR = TP / (TP + FN) (也就是Recall)
FPR = FP / (FP + TN)
举个栗子
假设你现在做机器学习笔试题,题目给了分类任务中的测试集标签和分类模型的预测结果,也就是给了Y_pred和Y_gt,让你手绘AUC曲线。Can you draw it?
答案一定是Yes, I can(看一下就会了)。
gt: [0, 1, 0, 1]. pred: [0.1, 0.35, 0.4, 0.8] 那么在阈值分别取{0.1, 0.35, 0.4, 0.8}的时候,分别判断出每个pred是TP/FP/TN/FP中的哪个,进而得出当前阈值下的TPR和FPR,也就是(FPR, TPR)这一ROC曲线图上的点;对于所有阈值都计算相应的(FPR, TPR),则得到完整的ROC曲线上的几个关键点,再连线(稍微脑补一下?)就得到完整ROC曲线。(再进一步,AUC也可以计算了,不是嘛?)
计算过程如下:

绘制得到的ROC曲线为:
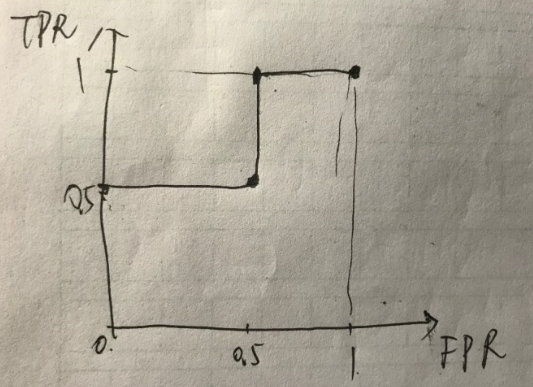
好吧,这个例子其实来自于如何绘制ROC曲线。
再举一个例子好了:
对于一组二元分类任务的测试集,其真实值为[0, 0, 0, 0, 1, 1, 1],模型预测为1的概率为[0.3, 0.2, 0.7, 0.5, 0.4, 0.9, 0.6],该模型在这个测试集上的ROC曲线为?(题目来源:sofasofa.io,一个有趣的机器学习社区,里面的机器学习题库)

对应的ROC曲线为:
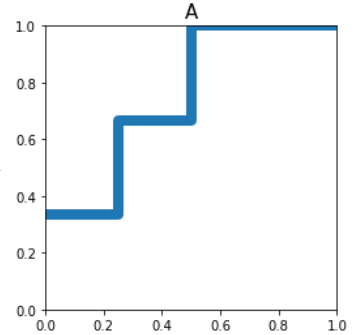
绘制ROC曲线的更多相关文章
- sklearn 绘制roc曲线
from sklearn.metrics import roc_curve, auc import matplotlib as mpl import matplotlib.pyplot as plt ...
- [机器学习]-分类问题常用评价指标、混淆矩阵及ROC曲线绘制方法
分类问题 分类问题是人工智能领域中最常见的一类问题之一,掌握合适的评价指标,对模型进行恰当的评价,是至关重要的. 同样地,分割问题是像素级别的分类,除了mAcc.mIoU之外,也可以采用分类问题的一些 ...
- R语言︱ROC曲线——分类器的性能表现评价
笔者寄语:分类器算法最后都会有一个预测精度,而预测精度都会写一个混淆矩阵,所有的训练数据都会落入这个矩阵中,而对角线上的数字代表了预测正确的数目,即True Positive+True Nagetiv ...
- ROC曲线,AUC面积
AUC(Area under Curve):Roc曲线下的面积,介于0.1和1之间.Auc作为数值可以直观的评价分类器的好坏,值越大越好. 首先AUC值是一个概率值,当你随机挑选一个正样本以及负样本, ...
- 分类器评估方法:ROC曲线
注:本文是人工智能研究网的学习笔记 ROC是什么 二元分类器(binary classifier)的分类结果 ROC空间 最好的预测模型在左上角,代表100%的灵敏度和0%的虚警率,被称为完美分类器. ...
- 评价指标的局限性、ROC曲线、余弦距离、A/B测试、模型评估的方法、超参数调优、过拟合与欠拟合
1.评价指标的局限性 问题1 准确性的局限性 准确率是分类问题中最简单也是最直观的评价指标,但存在明显的缺陷.比如,当负样本占99%时,分类器把所有样本都预测为负样本也可以获得99%的准确率.所以,当 ...
- ROC曲线与AUC
一.ROC曲线 1.简介 ROC曲线全称是"受试者工作特征曲线 "(Receiver Operating Characteristic curve),又称为感受性曲线(Sensit ...
- R语言绘图:ggplot2绘制ROC
使用ggplot2包绘制ROC曲线 rocplot<- function(pred, truth, ...){ predob<- prediction(pred, truth) #打印AU ...
- 机器学习:评价分类结果(ROC 曲线)
一.基础理解 1)定义 ROC(Receiver Operation Characteristic Curve) 定义:描述 TPR 和 FPR 之间的关系: 功能:应用于比较两个模型的优劣: 模型不 ...
随机推荐
- ROI Pool和ROI Align
这里说一下ROI Pool和ROI Align的区别: 一.ROI Pool层: 参考faster rcnn中的ROI Pool层,功能是将不同size的ROI区域映射到固定大小的feature ma ...
- Git学习笔记06-版本回退
在实际中,向版本库提交多次后,几千行代码肯定不记得每次都改了什么,可以使用git log来查看提交日志.也就是git commit -m 后面填写的这部分内容 也可以使用git log --pre ...
- VS2013 VS2015 VS2017调试出现无法启动iis express web服务器
最近老是遇到这个问题,天天如此,烦死人,网上答案繁多,但是都解决不了,也是由于各种环境不同导致的,这里把几种解决方法都记录下 一.其他项目都可以,就这么一个不行 因为其他项目都可以,就这么一个不行,所 ...
- windows类书的学习心得
原文网址:http://www.blogjava.net/sound/archive/2008/08/21/40499.html 现在的计算机图书发展的可真快,很久没去书店,昨日去了一下,真是感叹万千 ...
- UR#13 SRAND
总感觉这位大仙讲的很清楚:bztminamoto 题意 题目讲的是求 l~r 内所有数的次大质因子,这里设 f(x) 为 x 的次大质因子 我们差分一下就变成求两个前缀和信息了 按照套路,我们考虑 S ...
- MySQL--视图view、触发器trigger、事务(start transaction)、存储过程(特殊的数据逻辑处理函数)、流程控制(if,case....)
mysql致力于项目开发及数据库管理之间解耦合(帮忙封装一些数据处理方法,使应用程序的开发者可以专注于应用程序的开发),但受限于不同部门沟通的成本问题,现阶段直接使用的价值不大. 一.视图(只能sel ...
- Android直连SQL Server数据库
1. 下载jtds,一个开放源代码的Java实现的JDBC驱动,地址:http://sourceforge.net/projects/jtds/ 2. 添加jtds到当前Android项目中,本人使用 ...
- Python traceback的优雅处理
刚接触Python的时候,简单的异常处理已经可以帮助我们解决大多数问题,但是随着逐渐地深入,我们会发现有很多情况下简单的异常处理已经无法解决问题了,如下代码,单纯的打印异常所能提供的信息会非常有限. ...
- socket-WebSocket-HttpListener-TcpListener服务端客户端的具体使用案例
/// <summary> /// 启动服务监听的ip和端口的主线程 /// </summary> /// <param name="tunnelPort&qu ...
- HTML中特殊符号的处理
一.写在前面 今天在写页面时记不清大/小于符号该怎么写,于是就想着整理一下方便后面用到! 二.HTML中常用特殊符号的处理 < < 小于号或显示标记 > ...
