设计模式---数据结构模式之组合模式（Composite）

前提：数据结构模式

常常有一些组建在内部具有特定的数据结构，如果让客户程序依赖这些特定的数据结构，将极大的破坏组件的复用。这时候，将这些数据结构封装在内部，在外部提供统一的接口，来实现与特定数据结构无关的访问，是一种行之有效的解决方案。

典型模式

组合模式：Composite
迭代器模式：Iterator
责任链模式：Chain of Responsibility

一：组合模式

（一）概念

通过递归手段来构造树形对象结构并可以通过一个对象来访问整个对象

（二）动机

软件在某些情况下，客户代码过多地依赖于对象容器复杂的内部实现结构，对象容器内部实现结构（而非抽象接口）的变化将因其客户代码的频繁变化，带来了代码的维护性、扩展性等弊端。

如何将“客户代码与复杂的对象容器结构”解耦？让对象容器自己来实现自身的复杂结构，从而使得客户代码就像处理简单对象一样来处理复杂的对象容器？

（三）模式定义

将对象组合成树形结构以表示“部分-整体”的层级结构。Compisite使得用户对单个对象和组合对象的使用具有一致性 （稳定）。

                                                                              ——《设计模式》GoF

（四）代码讲解

1.抽象接口

class Component
{
public:
    virtual void process() = ;
    virtual ~Component(){}
};

2.两种类型之一：树形结构

//树节点
class Composite : public Component{

    string name;
    list<Component*> elements;　　//表达了一个树形结构
public:
    Composite(const string & s) : name(s) {}

    void add(Component* element) {
        elements.push_back(element);
    }
    void remove(Component* element){
        elements.remove(element);
    }

    void process(){
        //1. process current node

        //2. process leaf nodes
        for (auto &e : elements)　　//会出现多态递归调用，可能是树节点也可能是叶子节点
            e->process(); //多态调用
    }
};

2.两种类型之一：叶子节点

//叶子节点
class Leaf : public Component{
    string name;
public:
    Leaf(string s) : name(s) {}

    void process(){
        //process current node
    }
};

3.客户程序

void Invoke(Component & c){　　//可以是树节点或者叶子节点
    //...
    c.process();　　//多态调用
    //...
}

4.实现构建树

int main()
{

    Composite root("root");
    Composite treeNode1("treeNode1");
    Composite treeNode2("treeNode2");
    Composite treeNode3("treeNode3");
    Composite treeNode4("treeNode4");
    Leaf leat1("left1");
    Leaf leat2("left2");

    root.add(&treeNode1);
    treeNode1.add(&treeNode2);
    treeNode2.add(&leaf1);

    root.add(&treeNode3);
    treeNode3.add(&treeNode4);
    treeNode4.add(&leaf2);

    Invoke(root);
    Invoke(leaf2);
    Invoke(treeNode3);

}

问题：若是不用composite模式，如何实现？

//树节点
class Composite : public Component{

    string name;
    list<Component*> elements;
public:
    Composite(const string & s) : name(s) {}

    void add(Component* element) {
        elements.push_back(element);
    }
    void remove(Component* element){
        elements.remove(element);
    }

    void process(){

        //1. process current node
    }
};

//叶子节点
class Leaf : public Component{
    string name;
public:
    Leaf(string s) : name(s) {}

    void process(){
        //process current node
    }
};

会导致：

void Invoke(Component & c){
    //...
    c.process();　　//这个地方的处理要做分别处理，进行判断类别，然后进行递归，依赖于对象容器内部的复杂结构
    //...
}

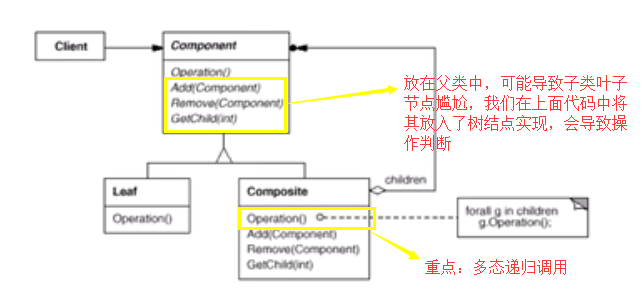
（五）类图（结构）

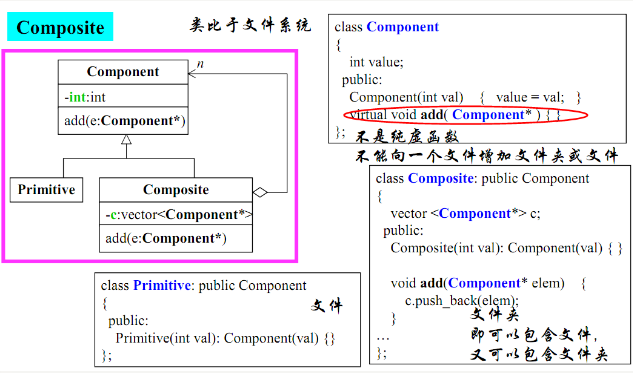
类比文件系统：

（六）要点总结

（一）Composite模式采用树形结构来实现普遍存在的对象容器，从而将“一对多”的关系转化为“一对一”的关系，使得客户代码可以一致地（复用）处理对象和对象容器，无需关心处理的是单个对象还是组合的对象容器。

若是不用composite模式，我们在Invoke中需要进行多种判断类型，是一对多，但是我们使用了composite模式，我们只需要使用一个process即可，无需更新内部是什么，统一处理

（二）将“客户代码与复杂的对象容器结构”解耦是Composite的核心思想，解耦之后，客户代码将与纯粹的抽象接口——而非对象容器的内部实现结构——发生依赖，从而更能“应对变化”。

（三）Composite模式在具体实现中，可以让父对象中的子对象反向追溯；如果父对象有频繁的遍历需求，可使用缓存技巧来改善效率

（七）案例实现（文件列表）

1.接口实现

//抽象接口
class Component
{
public:
    virtual void display() = ;
    virtual ~Component(){}
};

2.树形结构：文件夹

//树形结构,文件夹
class Folder :public Component
{
private:
    string f_name;
    list<Component*> f_list;
public:
    Folder(string name)
    {
        f_name = name;
    }

    virtual void display()
    {
        cout << "d\t" << f_name << endl;
        for (auto &f : f_list)
            f->display();
    }

    void Add(Component* comp)
    {
        f_list.push_back(comp);
    }

    void Remove(Component* comp)
    {
        f_list.remove(comp);
    }

    list<Component*> GetChild()
    {
        return f_list;
    }
};

3.叶子节点：文件夹

//叶子节点，文件
class File :public Component
{
private:
    string f_name;
public:
    File(string name)
    {
        f_name = name;
    }

    virtual void display()
    {
        cout << "f\t" << f_name << endl;
    }
};

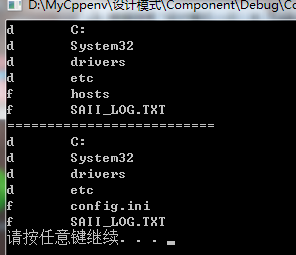
4.创建演示

void main()
{
    Folder* root = new Folder("C:");

    Folder* dir1 = new Folder("System32");
    Folder* dir2 = new Folder("drivers");
    Folder* dir3 = new Folder("etc");

    File* file1 = new File("SAII_LOG.TXT");
    File* file2 = new File("hosts");

    root->Add(dir1);
    dir1->Add(dir2);
    dir1->Add(file1);
    dir2->Add(dir3);
    dir3->Add(file2);

    root->display();
    cout << "==========================" << endl;
    dir3->Remove(file2);
    File* file3 = new File("config.ini");
    dir3->Add(file3);
    root->display();

    delete dir1;
    delete dir2;
    delete dir3;
    delete file1;
    delete file2;
    delete file3;

    system("pause");
    return;
}