LOJ#2722 情报中心

解:有个暴力是枚举两条链然后O(n)判定,可以得到15分。
还可以优化一下,枚举一条链,然后第二条链直接求两端点树上带权距离。可以做到O(m(n + m)),但是我用的树剖,跟上面那一档没啥区别Orz...
然后是链的部分,把所有链按照左端点小到大排序,左端点相同的时候按右端点小到大。
然后从右往左加。用一个树状数组维护前缀最大值。如果一个之前区间的左端点在我们当前区间的右端点内,就有交。
我们漏了一种情况:一个区间被另一个完全包含。于是新开一个树状数组维护即可。注意到这种情况在第一个树状数组中算出的答案不优,会被取代掉。
这样就有30分了。
/**
* There is no end though there is a start in space. ---Infinity.
* It has own power, it ruins, and it goes though there is a start also in the star. ---Finite.
* Only the person who was wisdom can read the most foolish one from the history.
* The fish that lives in the sea doesn't know the world in the land.
* It also ruins and goes if they have wisdom.
* It is funnier that man exceeds the speed of light than fish start living in the land.
* It can be said that this is an final ultimatum from the god to the people who can fight.
*
* Steins;Gate
*/ #include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) typedef long long LL;
const int N = ;
const LL INF = 9e18; struct Edge {
int nex, v;
LL len;
}edge[N << ]; int tp; struct Node {
int x, y;
LL z, val;
inline bool operator < (const Node &w) const {
if(x != w.x) return x < w.x;
return y < w.y;
}
}node[N]; int n, e[N], m, fa[N], deep[N];
int num, pos[N], son[N], siz[N], top[N];
LL Sum[N], sum[N << ], d[N], tag[N << ]; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].nex = e[x];
e[x] = tp;
return;
} void DFS_1(int x, int f) { /// get fa son siz d deep
fa[x] = f;
deep[x] = deep[f] + ;
siz[x] = ;
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
d[y] = d[x] + edge[i].len;
DFS_1(y, x);
siz[x] += siz[y];
if(siz[y] > siz[son[x]]) {
son[x] = y;
}
}
return;
} void DFS_2(int x, int f) { /// get top id pos
pos[x] = ++num;
top[x] = f;
Sum[num] = d[x] - d[fa[x]];
if(son[x]) {
DFS_2(son[x], f);
}
forson(x, i) {
int y = edge[i].v;
if(y == fa[x] || y == son[x]) continue;
DFS_2(y, y);
}
return;
} inline int lca(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
x = fa[top[x]];
}
else {
y = fa[top[y]];
}
}
return deep[x] < deep[y] ? x : y;
} inline LL dis(int x, int y) {
return d[x] + d[y] - * d[lca(x, y)];
} inline void pushdown(int l, int r, int o) {
if(tag[o] != -) {
if(tag[o] == ) {
sum[o << ] = sum[o << | ] = ;
}
else {
int mid = (l + r) >> ;
sum[o << ] = Sum[mid] - Sum[l - ];
sum[o << | ] = Sum[r] - Sum[mid];
}
tag[o << ] = tag[o << | ] = tag[o];
tag[o] = -;
}
return;
} void Add(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
sum[o] = Sum[r] - Sum[l - ];
tag[o] = ;
return;
}
int mid = (l + r) >> ;
pushdown(l, r, o);
if(L <= mid) Add(L, R, l, mid, o << );
if(mid < R) Add(L, R, mid + , r, o << | );
sum[o] = sum[o << ] + sum[o << | ];
return;
} LL ask(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
return sum[o];
}
int mid = (l + r) >> ;
pushdown(l, r, o);
LL ans = ;
if(L <= mid) {
ans += ask(L, R, l, mid, o << );
}
if(mid < R) {
ans += ask(L, R, mid + , r, o << | );
}
return ans;
} inline void Add(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
Add(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) Add(pos[x] + , pos[y], , n, );
return;
} inline LL ask(int x, int y) {
LL ans = ;
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
ans += ask(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) ans += ask(pos[x] + , pos[y], , n, );
return ans;
} inline void clear() {
memset(e + , , n * sizeof(int));
memset(son + , , n * sizeof(int));
tp = ;
num = ;
return;
}
/*
1
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8
*/ namespace Line {
LL ta[N], ta2[N];
inline LL ask(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta[i]);
}
return ans;
}
inline void Add(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta[i] = std::max(ta[i], v);
}
return;
}
inline LL ask2(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta2[i]);
}
return ans;
}
inline void Add2(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta2[i] = std::max(ta2[i], v);
}
return;
}
inline void solve() {
for(int i = ; i <= n; i++) ta2[i] = ta[i] = -INF;
LL ans = -INF;
std::sort(node + , node + m + );
for(int i = m; i >= ; i--) {
LL temp = ask(node[i].y - );
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val - Sum[node[i].y]);
}
temp = ask2(node[i].y);
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val);
}
Add(node[i].x, node[i].val + Sum[node[i].x]);
Add2(node[i].y, node[i].val + Sum[node[i].x] - Sum[node[i].y]);
}
if(ans == -INF) puts("F");
else {
printf("%lld\n", ans);
}
clear();
return;
}
}
/*
50
2
1 2 914572059
3
1 2 213930211
1 2 0
2 2 0
*/
inline void solve() { sum[] = tag[] = ; scanf("%d", &n);
LL z;
bool FLAG = ;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
if(y != x + ) {
FLAG = ;
}
} DFS_1(, );
DFS_2(, ); for(int i = ; i <= n; i++) {
Sum[i] += Sum[i - ];
} scanf("%d", &m);
for(int i = ; i <= m; i++) {
scanf("%d%d%lld", &node[i].x, &node[i].y, &node[i].z);
if(node[i].x > node[i].y) std::swap(node[i].x, node[i].y);
else if(node[i].x == node[i].y) {
m--;
i--;
}
node[i].val = dis(node[i].x, node[i].y) - node[i].z;
//printf("node %d [%d %d] val = %lld \n", i, node[i].x, node[i].y, node[i].val);
}
// solve
if(FLAG) {
Line::solve();
return;
} if(m > ) {
clear();
return;
} LL ans = -INF;
for(int i = ; i < m; i++) {
Add(node[i].x, node[i].y);
for(int j = i + ; j <= m; j++) {
/// choose i j
LL Val = ask(node[j].x, node[j].y);
//printf("Val = %lld \n", Val);
if(Val) {
ans = std::max(ans, node[i].val + node[j].val - Val);
}
}
tag[] = sum[] = ;
}
if(ans == -INF) {
puts("F");
}
else {
printf("%lld\n", ans);
}
clear();
return;
} int main() { int T;
scanf("%d", &T);
while(T--) solve();
return ;
}
30分代码
接下来还有c = 0的部分分:枚举每条边,统计所有过它的链中权值最大的两条更新答案。拿线段树合并实现。
#include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) typedef long long LL;
const int N = ;
const LL INF = 9e18; struct Edge {
int nex, v;
LL len;
}edge[N << ]; int tp; struct Node {
int x, y;
LL z, val;
inline bool operator < (const Node &w) const {
if(x != w.x) return x < w.x;
return y < w.y;
}
}node[N]; int n, e[N], m, fa[N], deep[N];
int num, pos[N], son[N], siz[N], top[N];
LL Sum[N], sum[N << ], d[N], tag[N << ]; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].nex = e[x];
e[x] = tp;
return;
} void DFS_1(int x, int f) { /// get fa son siz d deep
fa[x] = f;
deep[x] = deep[f] + ;
siz[x] = ;
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
d[y] = d[x] + edge[i].len;
DFS_1(y, x);
siz[x] += siz[y];
if(siz[y] > siz[son[x]]) {
son[x] = y;
}
}
return;
} void DFS_2(int x, int f) { /// get top id pos
pos[x] = ++num;
top[x] = f;
Sum[num] = d[x] - d[fa[x]];
if(son[x]) {
DFS_2(son[x], f);
}
forson(x, i) {
int y = edge[i].v;
if(y == fa[x] || y == son[x]) continue;
DFS_2(y, y);
}
return;
} inline int lca(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
x = fa[top[x]];
}
else {
y = fa[top[y]];
}
}
return deep[x] < deep[y] ? x : y;
} inline LL dis(int x, int y) {
return d[x] + d[y] - * d[lca(x, y)];
} inline void pushdown(int l, int r, int o) {
if(tag[o] != -) {
if(tag[o] == ) {
sum[o << ] = sum[o << | ] = ;
}
else {
int mid = (l + r) >> ;
sum[o << ] = Sum[mid] - Sum[l - ];
sum[o << | ] = Sum[r] - Sum[mid];
}
tag[o << ] = tag[o << | ] = tag[o];
tag[o] = -;
}
return;
} void Add(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
sum[o] = Sum[r] - Sum[l - ];
tag[o] = ;
return;
}
int mid = (l + r) >> ;
pushdown(l, r, o);
if(L <= mid) Add(L, R, l, mid, o << );
if(mid < R) Add(L, R, mid + , r, o << | );
sum[o] = sum[o << ] + sum[o << | ];
return;
} LL ask(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
return sum[o];
}
int mid = (l + r) >> ;
pushdown(l, r, o);
LL ans = ;
if(L <= mid) {
ans += ask(L, R, l, mid, o << );
}
if(mid < R) {
ans += ask(L, R, mid + , r, o << | );
}
return ans;
} inline void Add(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
Add(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) Add(pos[x] + , pos[y], , n, );
return;
} inline LL ask(int x, int y) {
LL ans = ;
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
ans += ask(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) ans += ask(pos[x] + , pos[y], , n, );
return ans;
} inline void clear() {
memset(e + , , n * sizeof(int));
memset(son + , , n * sizeof(int));
tp = ;
num = ;
return;
}
/*
1
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8
*/ namespace Line {
LL ta[N], ta2[N];
inline LL ask(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta[i]);
}
return ans;
}
inline void Add(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta[i] = std::max(ta[i], v);
}
return;
}
inline LL ask2(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta2[i]);
}
return ans;
}
inline void Add2(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta2[i] = std::max(ta2[i], v);
}
return;
}
inline void solve() {
for(int i = ; i <= n; i++) ta2[i] = ta[i] = -INF;
LL ans = -INF;
std::sort(node + , node + m + );
for(int i = m; i >= ; i--) {
LL temp = ask(node[i].y - );
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val - Sum[node[i].y]);
}
temp = ask2(node[i].y);
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val);
}
Add(node[i].x, node[i].val + Sum[node[i].x]);
Add2(node[i].y, node[i].val + Sum[node[i].x] - Sum[node[i].y]);
}
if(ans == -INF) puts("F");
else {
printf("%lld\n", ans);
}
return;
}
} namespace C0 {
int rt[N], xx;
LL Ans, X[N];
std::vector<int> v[N];
namespace seg {
const int M = ;
int ls[M], rs[M], tot, cnt[M];
LL sum[M];
void insert(int p, int v, int l, int r, int &o) {
if(!o) {
o = ++tot;
sum[o] = cnt[o] = ls[o] = rs[o] = ;
}
if(l == r) {
sum[o] += v * X[r];
cnt[o] += v;
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
insert(p, v, l, mid, ls[o]);
}
else {
insert(p, v, mid + , r, rs[o]);
}
sum[o] = sum[ls[o]] + sum[rs[o]];
cnt[o] = cnt[ls[o]] + cnt[rs[o]];
return;
}
LL ask(int k, int l, int r, int o) {
if(l == r) {
return k * X[r];
}
int mid = (l + r) >> ;
if(k <= cnt[rs[o]]) {
return ask(k, mid + , r, rs[o]);
}
else {
return ask(k - cnt[rs[o]], l, mid, ls[o]) + sum[rs[o]];
}
}
inline LL Ask(int x) {
if(cnt[rt[x]] < ) return -INF;
return ask(, , xx, rt[x]);
}
int merge(int x, int y) {
if(!x || !y) return x | y;
sum[x] += sum[y];
cnt[x] += cnt[y];
ls[x] = merge(ls[x], ls[y]);
rs[x] = merge(rs[x], rs[y]);
return x;
}
inline void Merge(int x, int y) {
rt[x] = merge(rt[x], rt[y]);
return;
}
}
void DFS(int x, int f) {
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS(y, x);
Ans = std::max(Ans, seg::Ask(y));
seg::Merge(x, y);
}
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
if(t > ) {
seg::insert(t, , , xx, rt[x]);
}
else {
seg::insert(-t, -, , xx, rt[x]);
}
}
return;
}
inline void solve() {
memset(rt + , , n * sizeof(int));
seg::tot = ;
Ans = -INF;
for(int i = ; i <= n; i++) v[i].clear();
for(int i = ; i <= m; i++) {
X[i] = node[i].val;
}
std::sort(X + , X + m + );
xx = std::unique(X + , X + m + ) - X - ;
for(int i = ; i <= m; i++) {
int val = std::lower_bound(X + , X + xx + , node[i].val) - X;
int x = node[i].x, y = node[i].y, z = lca(node[i].x, node[i].y);
v[x].push_back(val);
v[y].push_back(val);
v[z].push_back(-val);
v[z].push_back(-val);
}
DFS(, );
if(Ans == -INF) puts("F");
else printf("%lld\n", Ans);
return;
}
} /*
50
2
1 2 914572059
3
1 2 213930211
1 2 0
2 2 0
*/
inline void solve() { sum[] = tag[] = ; scanf("%d", &n);
LL z;
bool FLAG = , c0 = ;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
if(z) c0 = ;
if(y != x + ) {
FLAG = ;
}
} DFS_1(, );
DFS_2(, ); for(int i = ; i <= n; i++) {
Sum[i] += Sum[i - ];
} scanf("%d", &m);
for(int i = ; i <= m; i++) {
scanf("%d%d%lld", &node[i].x, &node[i].y, &node[i].z);
if(node[i].x > node[i].y) std::swap(node[i].x, node[i].y);
else if(node[i].x == node[i].y) {
m--;
i--;
}
node[i].val = dis(node[i].x, node[i].y) - node[i].z;
//printf("node %d [%d %d] val = %lld \n", i, node[i].x, node[i].y, node[i].val);
}
// solve
if(FLAG) {
Line::solve();
clear();
return;
}
if(c0) {
C0::solve();
clear();
return;
} if(m > ) {
clear();
return;
} LL ans = -INF;
for(int i = ; i < m; i++) {
Add(node[i].x, node[i].y);
for(int j = i + ; j <= m; j++) {
/// choose i j
LL Val = ask(node[j].x, node[j].y);
//printf("Val = %lld \n", Val);
if(Val) {
ans = std::max(ans, node[i].val + node[j].val - Val);
}
}
tag[] = sum[] = ;
}
if(ans == -INF) {
puts("F");
}
else {
printf("%lld\n", ans);
}
clear();
return;
} int main() { int T;
scanf("%d", &T);
while(T--) solve();
return ;
}
45分代码
接下来是这个东西...

然而我只得到了20分...可能比较丑。
只枚举有公共部分的链:考虑枚举每条边,并m2枚举经过这条边的链。
这样两条链可能会在多条边上算多次,于是我们限定某一个链的lca是这条边的上端点。
具体一点,线段树合并搞出经过每条边的链,然后枚举以这条边为lca的链,预处理树上距离。然后枚举经过这条边的所有链,并更新答案。
其实可以O(1)lca和长链剖分O(1)k级祖先来优化,但是我已经写不动啦......
/**
* There is no end though there is a start in space. ---Infinity.
* It has own power, it ruins, and it goes though there is a start also in the star. ---Finite.
* Only the person who was wisdom can read the most foolish one from the history.
* The fish that lives in the sea doesn't know the world in the land.
* It also ruins and goes if they have wisdom.
* It is funnier that man exceeds the speed of light than fish start living in the land.
* It can be said that this is an final ultimatum from the god to the people who can fight.
*
* Steins;Gate
*/ #include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) typedef long long LL;
const int N = , M = ;
const LL INF = 9e18; struct Edge {
int nex, v;
LL len;
bool vis;
}edge[N << ]; int tp = ; struct Node {
int x, y;
LL z, val;
inline bool operator < (const Node &w) const {
if(x != w.x) return x < w.x;
return y < w.y;
}
}node[N]; int n, e[N], m, fa[N], deep[N], ls[M], rs[M], tot;
int num, pos[N], son[N], siz[N], top[N], rt[N], pw[N];
LL Sum[N], sum[N << ], d[N], tag[N << ]; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].vis = ;
edge[tp].nex = e[x];
e[x] = tp;
return;
} void DFS_1(int x, int f) { /// get fa son siz d deep
fa[x] = f;
deep[x] = deep[f] + ;
siz[x] = ;
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
d[y] = d[x] + edge[i].len;
DFS_1(y, x);
siz[x] += siz[y];
if(siz[y] > siz[son[x]]) {
son[x] = y;
}
}
return;
} void DFS_2(int x, int f) { /// get top id pos
pos[x] = ++num;
top[x] = f;
Sum[num] = d[x] - d[fa[x]];
if(son[x]) {
DFS_2(son[x], f);
}
forson(x, i) {
int y = edge[i].v;
if(y == fa[x] || y == son[x]) continue;
DFS_2(y, y);
}
return;
} inline int lca(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
x = fa[top[x]];
}
else {
y = fa[top[y]];
}
}
return deep[x] < deep[y] ? x : y;
} inline LL dis(int x, int y) {
return d[x] + d[y] - * d[lca(x, y)];
} inline void pushdown(int l, int r, int o) {
if(tag[o] != -) {
if(tag[o] == ) {
sum[o << ] = sum[o << | ] = ;
}
else {
int mid = (l + r) >> ;
sum[o << ] = Sum[mid] - Sum[l - ];
sum[o << | ] = Sum[r] - Sum[mid];
}
tag[o << ] = tag[o << | ] = tag[o];
tag[o] = -;
}
return;
} void Add(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
sum[o] = Sum[r] - Sum[l - ];
tag[o] = ;
return;
}
int mid = (l + r) >> ;
pushdown(l, r, o);
if(L <= mid) Add(L, R, l, mid, o << );
if(mid < R) Add(L, R, mid + , r, o << | );
sum[o] = sum[o << ] + sum[o << | ];
return;
} LL ask(int L, int R, int l, int r, int o) {
if(L <= l && r <= R) {
return sum[o];
}
int mid = (l + r) >> ;
pushdown(l, r, o);
LL ans = ;
if(L <= mid) {
ans += ask(L, R, l, mid, o << );
}
if(mid < R) {
ans += ask(L, R, mid + , r, o << | );
}
return ans;
} inline void Add(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
Add(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) Add(pos[x] + , pos[y], , n, );
return;
} inline LL ask(int x, int y) {
LL ans = ;
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) {
std::swap(x, y);
}
ans += ask(pos[top[y]], pos[y], , n, );
y = fa[top[y]];
}
if(deep[x] > deep[y]) std::swap(x, y);
if(x != y) ans += ask(pos[x] + , pos[y], , n, );
return ans;
} inline void clear() {
memset(e + , , n * sizeof(int));
memset(son + , , n * sizeof(int));
tp = ;
num = ;
return;
}
/*
1
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8
*/ namespace Line {
LL ta[N], ta2[N];
inline LL ask(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta[i]);
}
return ans;
}
inline void Add(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta[i] = std::max(ta[i], v);
}
return;
}
inline LL ask2(int i) {
LL ans = -INF;
for(; i; i -= i & (-i)) {
ans = std::max(ans, ta2[i]);
}
return ans;
}
inline void Add2(int i, LL v) {
for(; i <= n; i += i & (-i)) {
ta2[i] = std::max(ta2[i], v);
}
return;
}
inline void solve() {
for(int i = ; i <= n; i++) ta2[i] = ta[i] = -INF;
LL ans = -INF;
std::sort(node + , node + m + );
for(int i = m; i >= ; i--) {
LL temp = ask(node[i].y - );
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val - Sum[node[i].y]);
}
temp = ask2(node[i].y);
if(temp != -INF) {
ans = std::max(ans, temp + node[i].val);
}
Add(node[i].x, node[i].val + Sum[node[i].x]);
Add2(node[i].y, node[i].val + Sum[node[i].x] - Sum[node[i].y]);
}
if(ans == -INF) puts("F");
else {
printf("%lld\n", ans);
}
return;
}
} namespace C0 {
int xx;
LL Ans, X[N];
std::vector<int> v[N];
namespace seg {
int cnt[M];
LL sum[M];
void insert(int p, int v, int l, int r, int &o) {
if(!o) {
o = ++tot;
sum[o] = cnt[o] = ls[o] = rs[o] = ;
}
if(l == r) {
sum[o] += v * X[r];
cnt[o] += v;
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
insert(p, v, l, mid, ls[o]);
}
else {
insert(p, v, mid + , r, rs[o]);
}
sum[o] = sum[ls[o]] + sum[rs[o]];
cnt[o] = cnt[ls[o]] + cnt[rs[o]];
return;
}
LL ask(int k, int l, int r, int o) {
if(l == r) {
return k * X[r];
}
int mid = (l + r) >> ;
if(k <= cnt[rs[o]]) {
return ask(k, mid + , r, rs[o]);
}
else {
return ask(k - cnt[rs[o]], l, mid, ls[o]) + sum[rs[o]];
}
}
inline LL Ask(int x) {
if(cnt[rt[x]] < ) return -INF;
return ask(, , xx, rt[x]);
}
int merge(int x, int y) {
if(!x || !y) return x | y;
sum[x] += sum[y];
cnt[x] += cnt[y];
ls[x] = merge(ls[x], ls[y]);
rs[x] = merge(rs[x], rs[y]);
return x;
}
inline void Merge(int x, int y) {
rt[x] = merge(rt[x], rt[y]);
return;
}
}
void DFS(int x, int f) {
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS(y, x);
Ans = std::max(Ans, seg::Ask(y));
seg::Merge(x, y);
}
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
if(t > ) {
seg::insert(t, , , xx, rt[x]);
}
else {
seg::insert(-t, -, , xx, rt[x]);
}
}
return;
}
inline void solve() {
memset(rt + , , n * sizeof(int));
tot = ;
Ans = -INF;
for(int i = ; i <= n; i++) v[i].clear();
for(int i = ; i <= m; i++) {
X[i] = node[i].val;
}
std::sort(X + , X + m + );
xx = std::unique(X + , X + m + ) - X - ;
for(int i = ; i <= m; i++) {
int val = std::lower_bound(X + , X + xx + , node[i].val) - X;
int x = node[i].x, y = node[i].y, z = lca(node[i].x, node[i].y);
v[x].push_back(val);
v[y].push_back(val);
v[z].push_back(-val);
v[z].push_back(-val);
}
DFS(, );
if(Ans == -INF) puts("F");
else printf("%lld\n", Ans);
return;
}
} namespace tbf {
LL d2[N], Ans;
int Top, stk[N], stk2[N], Top2, faa[N][];
std::vector<int> vx[N], v[N];
LL dis2(int x, int y) {
return d2[x] + d2[y] - * d2[lca(x, y)];
}
void DFS_3(int x, int f) { /// get dis2
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
d2[y] = d2[x] + edge[i].len * edge[i].vis;
DFS_3(y, x);
}
return;
}
bool DFS_4(int x, int f, int t) { /// visit a link
if(x == t) {
Top = ;
return true;
}
forson(x, i) {
int y = edge[i].v;
if(y == f) {
continue;
}
if(DFS_4(y, x, t)) {
edge[i].vis = edge[i ^ ].vis = ;
stk[++Top] = i;
return true;
}
}
return false;
}
namespace seg {
int sum[M];
void insert(int p, int v, int l, int r, int &o) {
if(!o) {
o = ++tot;
ls[o] = rs[o] = sum[o] = ;
}
if(l == r) {
sum[o] += v;
return;
}
int mid = (l + r) >> ;
if(p <= mid) insert(p, v, l, mid, ls[o]);
else insert(p, v, mid + , r, rs[o]);
sum[o] = sum[ls[o]] + sum[rs[o]];
return;
}
void solve(int l, int r, int o) {
if(l == r) {
stk2[++Top2] = r;
return;
}
int mid = (l + r) >> ;
if(sum[ls[o]]) {
solve(l, mid, ls[o]);
}
if(sum[rs[o]]) {
solve(mid + , r, rs[o]);
}
return;
}
int merge(int x, int y) {
if(!x || !y) return x | y;
sum[x] += sum[y];
ls[x] = merge(ls[x], ls[y]);
rs[x] = merge(rs[x], rs[y]);
return x;
}
} void DFS_5(int x, int f) {
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS_5(y, x);
Top2 = ;
seg::solve(, m, rt[y]);
for(int j = ; j < (int)vx[y].size(); j++) {
int z = vx[y][j];
/// link z
DFS_4(node[z].x, , node[z].y);
DFS_3(, );
for(int k = ; k <= Top2; k++) {
int w = stk2[k]; /// link w
if(w == z) continue;
Ans = std::max(Ans, node[z].val + node[w].val - dis2(node[w].x, node[w].y));
}
while(Top) {
edge[stk[Top]].vis = edge[stk[Top] ^ ].vis = ;
Top--;
}
}
rt[x] = seg::merge(rt[x], rt[y]);
}
/// insert
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
if(t > ) {
seg::insert(t, , , m, rt[x]);
}
else {
seg::insert(-t, -, , m, rt[x]);
}
}
return;
}
void DFS_6(int x, int f) {
faa[x][] = f;
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS_6(y, x);
}
return;
}
inline void prework() {
for(int j = ; j <= pw[n]; j++) {
for(int i = ; i <= n; i++) {
faa[i][j] = faa[faa[i][j - ]][j - ];
}
}
return;
}
inline int Find(int x, int z) {
int t = pw[n];
while(t >= && fa[x] != z) {
if(deep[faa[x][t]] > deep[z]) {
x = faa[x][t];
}
t--;
}
return x;
}
inline void solve() {
tot = ;
Ans = -INF;
memset(rt + , , n * sizeof(int));
for(int i = ; i <= n; i++) {
v[i].clear();
vx[i].clear();
}
DFS_6(, );
prework();
for(int i = ; i <= m; i++) {
int x = node[i].x, y = node[i].y, z = lca(x, y);
v[x].push_back(i);
v[y].push_back(i);
v[z].push_back(-i);
v[z].push_back(-i);
if(x != z) {
int xx = Find(x, z);
vx[xx].push_back(i);
}
if(y != z) {
int yy = Find(y, z);
vx[yy].push_back(i);
}
}
DFS_5(, );
if(Ans == -INF) puts("F");
else printf("%lld\n", Ans);
return;
}
} /** namespace tbf */ inline void solve() { sum[] = tag[] = ; scanf("%d", &n);
LL z;
bool FLAG = , c0 = ;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
if(z) c0 = ;
if(y != x + ) {
FLAG = ;
}
} DFS_1(, );
DFS_2(, ); for(int i = ; i <= n; i++) {
Sum[i] += Sum[i - ];
} scanf("%d", &m);
for(int i = ; i <= m; i++) {
scanf("%d%d%lld", &node[i].x, &node[i].y, &node[i].z);
if(node[i].x > node[i].y) std::swap(node[i].x, node[i].y);
else if(node[i].x == node[i].y) {
m--;
i--;
}
node[i].val = dis(node[i].x, node[i].y) - node[i].z;
//printf("node %d [%d %d] val = %lld \n", i, node[i].x, node[i].y, node[i].val);
}
// solve tbf::solve();
clear();
return; if(FLAG) {
Line::solve();
clear();
return;
}
if(c0) {
C0::solve();
clear();
return;
} if(m > ) {
tbf::solve();
clear();
return;
} LL ans = -INF;
for(int i = ; i < m; i++) {
Add(node[i].x, node[i].y);
for(int j = i + ; j <= m; j++) {
/// choose i j
LL Val = ask(node[j].x, node[j].y);
//printf("Val = %lld \n", Val);
if(Val) {
ans = std::max(ans, node[i].val + node[j].val - Val);
}
}
tag[] = sum[] = ;
}
if(ans == -INF) {
puts("F");
}
else {
printf("%lld\n", ans);
}
clear();
return;
} int main() { for(int i = ; i < N; i++) pw[i] = pw[i >> ] + ; int T;
scanf("%d", &T);
while(T--) solve();
return ;
}
20分真暴力代码
接下来是S1的部分分:所有lca全部不同。

实际上(参考yww的代码)我们要维护两个东西,一个是val最大值,一个是val + d[lca]的最大值。然后更新的时候,把线段树交错更新。
也就是说左儿子(较浅)的val + 右儿子(较深)的(val + d[lca])然后减去红点的深度。
然后我们要在插入和merge的同时更新。注意到我们还有一个删除操作,x子树搞完之后,深度大于等于x的全部失效,也就是我们要把线段树右边的一段全部清除。
DFS那里插入删除merge的顺序非常重要....反正我试了很久才搞对顺序。
#include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) typedef long long LL;
const int N = ;
const LL INF = 4e18; struct Edge {
int nex, v;
LL len;
}edge[N << ]; int tp = ; struct Node {
int x, y, w;
LL val, z;
}node[N]; int e[N], num2, pos2[N], ST[N][], pw[N], deep[N], n, m, fa[N];
LL d[N];
std::bitset<N> visLca; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].nex = e[x];
e[x] = tp;
return;
} inline void clear() {
memset(e + , , n * sizeof(int));
visLca.reset();
tp = ;
num2 = ;
return;
} void DFS(int x, int f) {
pos2[x] = ++num2;
ST[num2][] = x;
deep[x] = deep[f] + ;
fa[x] = f;
forson(x, i) {
int y = edge[i].v;
if(y == f) {
continue;
}
d[y] = d[x] + edge[i].len;
DFS(y, x);
ST[++num2][] = x;
}
return;
} inline void prework() {
for(int j = ; j <= pw[num2]; j++) {
for(int i = ; i + ( << j) - <= num2; i++) {
if(deep[ST[i][j - ]] < deep[ST[i + ( << (j - ))][j - ]]) {
ST[i][j] = ST[i][j - ];
}
else {
ST[i][j] = ST[i + ( << (j - ))][j - ];
}
}
}
return;
} inline int lca(int x, int y) {
x = pos2[x];
y = pos2[y];
if(x > y) std::swap(x, y);
int t = pw[y - x + ];
if(deep[ST[x][t]] < deep[ST[y - ( << t) + ][t]]) {
return ST[x][t];
}
else {
return ST[y - ( << t) + ][t];
}
} inline LL dis(int x, int y) {
return d[x] + d[y] - * d[lca(x, y)];
} namespace Sone { /// lca != lca
LL Ans;
int rt[N];
std::vector<int> v[N];
namespace seg {
const int M = ; int ls[M], rs[M], tot;
LL large[M], largeD[M]; inline void pushup(int o) {
large[o] = std::max(large[ls[o]], large[rs[o]]);
largeD[o] = std::max(largeD[ls[o]], largeD[rs[o]]);
return;
}
void insert(int p, LL v, LL v2, LL v3, int l, int r, int &o) {
if(!o) {
o = ++tot;
ls[o] = rs[o] = ;
large[o] = largeD[o] = -INF;
}
if(l == r) {
large[o] = std::max(large[o], v);
largeD[o] = std::max(largeD[o], v + v2);
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
Ans = std::max(Ans, largeD[rs[o]] + v - v3);
insert(p, v, v2, v3, l, mid, ls[o]);
}
else {
Ans = std::max(Ans, large[ls[o]] + v + v2 - v3);
insert(p, v, v2, v3, mid + , r, rs[o]);
}
pushup(o);
return;
}
int merge(int x, int y, LL v) {
//printf("merge x = %d y = %d v = %lld \n", x, y, v);
if(!x || !y) return x | y;
Ans = std::max(Ans, std::max(large[ls[x]] + largeD[rs[y]], large[ls[y]] + largeD[rs[x]]) - v);
large[x] = std::max(large[x], large[y]);
largeD[x] = std::max(largeD[x], largeD[y]);
ls[x] = merge(ls[x], ls[y], v);
rs[x] = merge(rs[x], rs[y], v);
return x;
}
void del(int p, int l, int r, int o) {
if(!o) {
return;
}
if(l == r) {
large[o] = largeD[o] = -INF;
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
large[rs[o]] = largeD[rs[o]] = -INF;
del(p, l, mid, ls[o]);
}
else {
del(p, mid + , r, rs[o]);
}
pushup(o);
return;
}
} void DFS_1(int x, int f) {
//printf("x = %d \n", x);
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
//printf("x = %d insert p = %d w = %d v1 = %lld v2 = %lld \n", x, deep[node[t].w], node[t].w, node[t].val, d[node[t].w]);
seg::insert(deep[node[t].w], node[t].val, d[node[t].w], d[x], , n, rt[x]);
}
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
//printf("y = %d \n", y);
DFS_1(y, x);
//printf("merge %d -> %d \n", x, y);
seg::del(deep[x], , n, rt[y]);
rt[x] = seg::merge(rt[x], rt[y], d[x]);
//printf("Ans = %lld \n", Ans);
}
return;
} inline void solve() {
seg::tot = ;
seg::large[] = seg::largeD[] = -INF;
Ans = -INF;
memset(rt + , , n * sizeof(int));
for(int i = ; i <= n; i++) v[i].clear(); for(int i = ; i <= m; i++) {
int x = node[i].x, y = node[i].y, z = node[i].w;
if(x != z) {
v[x].push_back(i);
}
if(y != z) {
v[y].push_back(i);
}
} DFS_1(, );
if(Ans < (LL)(-3e18)) puts("F");
else printf("%lld\n", Ans);
return;
}
} namespace Stwo { /// lca = 1
inline void solve() { return;
}
} inline void solve() {
scanf("%d", &n);
LL z;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
} DFS(, );
prework(); scanf("%d", &m);
bool S1 = true, S2 = true;
int lastLca = -;
for(int i = , x, y; i <= m; i++) {
scanf("%d%d%lld", &x, &y, &z);
node[i].x = x;
node[i].y = y;
node[i].z = z;
node[i].val = dis(x, y) - z;
int temp = lca(x, y);
if(lastLca == -) lastLca = temp;
else if(lastLca != temp) S2 = false;
if(visLca[temp]) S1 = false;
else visLca.set(temp);
node[i].w = temp;
} if(S1) {
Sone::solve();
return;
}
if(S2) {
Stwo::solve();
return;
} return;
} int main() { freopen("in.in", "r", stdin);
freopen("my.out", "w", stdout); for(int i = ; i < N; i++) pw[i] = pw[i >> ] + ; int T;
scanf("%d", &T);
while(T--) {
solve();
if(T) clear();
}
return ;
}
15分S1代码
接下来是S2的lca全部为1的部分分。
继续抄题解。
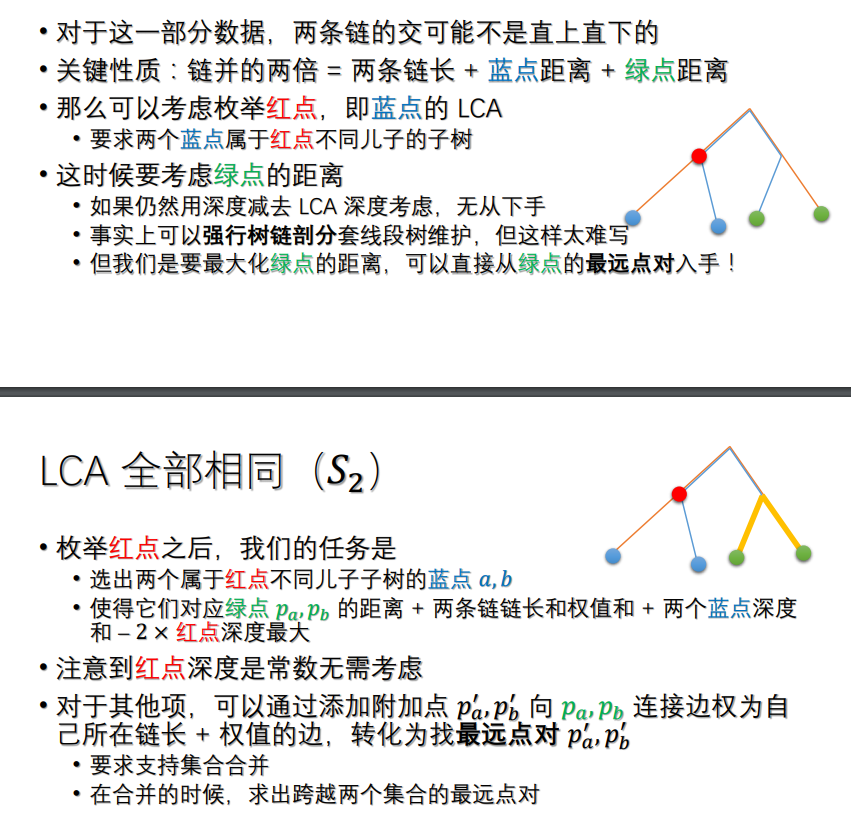
我的理解是,首先把2 * 总价值转化成链长之和 - 代价之和 + 蓝点距离 + 绿点距离。我们尝试新建两个点来表示出这个东西。
首先把蓝点距离转化成蓝a深度 + 蓝b深度 - 2 * 红点深度。
对于一条链a,我们在绿a处挂上一个节点绿a',使得它到绿a的距离为链长 - 代价 + 蓝a深度。
然后我们发现,这样两个附加点的距离正好凑出了上面那个2 * 总价值,只要再减去2 * 红点深度就行了。

有这个结论是因为边权非负。那么我们新加的边不是有一堆负权吗?为什么成立呢?
因为我们可以给这些新加的边(假装加上了)加上一个很大的正值来达到非负。为什么这个方法在一般的树上不适用呢?因为我们不知道直径上有多少条边加了这个大正值。但是本题中会有恰两条边加上这个正值。
所以做法就出来了。具体来说,我们DFS这棵树,然后在每个蓝a处把绿a'加入点集,同理在绿a处把蓝a'加入点集。
然后合并点集的同时更新答案。注意当前点为根的时候不能更新,因为可能会把蓝a'和绿a'的距离算入答案。也没必要更新,因为根不可能作为红点。
注意只需要挂可能成为蓝a的对应的绿a',就是说一条链直上直下的时候有一个点不用加。
#include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) using namespace std; typedef long long LL;
const int N = ;
const LL INF = 4e18; struct Edge {
int nex, v;
LL len;
}edge[N << ]; int tp = ; struct Node {
int x, y, w;
LL val, z;
}node[N]; struct Data {
int a, b;
Data(int A = , int B = ) : a(A), b(B) {}
}data[N]; int e[N], num2, pos2[N], ST[N][], pw[N], deep[N], n, m, fa[N], fr[N];
LL d[N];
std::bitset<N> visLca; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].nex = e[x];
e[x] = tp;
return;
} inline void clear() {
memset(e + , , n * sizeof(int));
visLca.reset();
tp = ;
num2 = ;
return;
} void DFS(int x, int f) {
pos2[x] = ++num2;
ST[num2][] = x;
deep[x] = deep[f] + ;
fa[x] = f;
forson(x, i) {
int y = edge[i].v;
if(y == f) {
continue;
}
d[y] = d[x] + edge[i].len;
DFS(y, x);
ST[++num2][] = x;
}
return;
} inline void prework() {
for(int j = ; j <= pw[num2]; j++) {
for(int i = ; i + ( << j) - <= num2; i++) {
if(deep[ST[i][j - ]] < deep[ST[i + ( << (j - ))][j - ]]) {
ST[i][j] = ST[i][j - ];
}
else {
ST[i][j] = ST[i + ( << (j - ))][j - ];
}
}
}
return;
} inline int lca(int x, int y) {
x = pos2[fr[x]];
y = pos2[fr[y]];
if(x > y) std::swap(x, y);
int t = pw[y - x + ];
if(deep[ST[x][t]] < deep[ST[y - ( << t) + ][t]]) {
return ST[x][t];
}
else {
return ST[y - ( << t) + ][t];
}
} inline LL dis(int x, int y) {
if(!x || !y) return -INF;
if(x > n && (x - n + ) / == (y - n + ) / ) return -INF;
//if(x > n) printf("dis %d %d = %lld \n", x, y, d[x] + d[y] - 2 * d[lca(x, y)]);
return d[x] + d[y] - * d[lca(x, y)];
} namespace Sone { /// lca != lca
LL Ans;
int rt[N];
std::vector<int> v[N];
namespace seg {
const int M = ; int ls[M], rs[M], tot;
LL large[M], largeD[M]; inline void pushup(int o) {
large[o] = std::max(large[ls[o]], large[rs[o]]);
largeD[o] = std::max(largeD[ls[o]], largeD[rs[o]]);
return;
}
void insert(int p, LL v, LL v2, LL v3, int l, int r, int &o) {
if(!o) {
o = ++tot;
ls[o] = rs[o] = ;
large[o] = largeD[o] = -INF;
}
if(l == r) {
large[o] = std::max(large[o], v);
largeD[o] = std::max(largeD[o], v + v2);
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
Ans = std::max(Ans, largeD[rs[o]] + v - v3);
insert(p, v, v2, v3, l, mid, ls[o]);
}
else {
Ans = std::max(Ans, large[ls[o]] + v + v2 - v3);
insert(p, v, v2, v3, mid + , r, rs[o]);
}
pushup(o);
return;
}
int merge(int x, int y, LL v) {
//printf("merge x = %d y = %d v = %lld \n", x, y, v);
if(!x || !y) return x | y;
Ans = std::max(Ans, std::max(large[ls[x]] + largeD[rs[y]], large[ls[y]] + largeD[rs[x]]) - v);
large[x] = std::max(large[x], large[y]);
largeD[x] = std::max(largeD[x], largeD[y]);
ls[x] = merge(ls[x], ls[y], v);
rs[x] = merge(rs[x], rs[y], v);
return x;
}
void del(int p, int l, int r, int o) {
if(!o) {
return;
}
if(l == r) {
large[o] = largeD[o] = -INF;
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
large[rs[o]] = largeD[rs[o]] = -INF;
del(p, l, mid, ls[o]);
}
else {
del(p, mid + , r, rs[o]);
}
pushup(o);
return;
}
} void DFS_1(int x, int f) {
//printf("x = %d \n", x);
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
//printf("x = %d insert p = %d w = %d v1 = %lld v2 = %lld \n", x, deep[node[t].w], node[t].w, node[t].val, d[node[t].w]);
seg::insert(deep[node[t].w], node[t].val, d[node[t].w], d[x], , n, rt[x]);
}
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
//printf("y = %d \n", y);
DFS_1(y, x);
//printf("merge %d -> %d \n", x, y);
seg::del(deep[x], , n, rt[y]);
rt[x] = seg::merge(rt[x], rt[y], d[x]);
//printf("Ans = %lld \n", Ans);
}
return;
} inline void solve() {
seg::tot = ;
seg::large[] = seg::largeD[] = -INF;
Ans = -INF;
memset(rt + , , n * sizeof(int));
for(int i = ; i <= n; i++) v[i].clear(); for(int i = ; i <= m; i++) {
int x = node[i].x, y = node[i].y, z = node[i].w;
if(x != z) {
v[x].push_back(i);
}
if(y != z) {
v[y].push_back(i);
}
} DFS_1(, );
if(Ans < (LL)(-3e18)) puts("F");
else printf("%lld\n", Ans);
return;
}
} namespace Stwo { /// lca = 1
/*Edge EDGE[N << 1]; int TP;
int E[N], use[N], Time, fr[N];
inline void ADD(int x, int y, LL z) {
TP++;
EDGE[TP].v = y;
EDGE[TP].len = z;
EDGE[TP].nex = E[x];
E[x] = TP;
return;
}
inline void work(int x) {
if(use[x] != Time) {
use[x] = Time;
E[x] = 0;
? = ?;
}
return;
}*/
std::vector<int> v[N];
LL Ans; inline void update(Data &x, const Data &y, const LL &v) {
//printf("update v = %lld \n", v);
LL d12 = dis(x.a, x.b), d34 = dis(y.a, y.b);
LL d13 = dis(x.a, y.a), d14 = dis(x.a, y.b);
LL d23 = dis(x.b, y.a), d24 = dis(x.b, y.b);
Ans = std::max(Ans, std::max(std::max(d13, d14), std::max(d23, d24)) - v);
int xa = x.a, xb = x.b;
if(d34 > d12) {
x = y;
d12 = d34;
}
if(d13 > d12) {
x = Data(xa, y.a);
d12 = d13;
}
if(d14 > d12) {
x = Data(xa, y.b);
d12 = d14;
}
if(d23 > d12) {
x = Data(xb, y.a);
d12 = d23;
}
if(d24 > d12) {
x = Data(xb, y.b);
}
if(!x.a) x = y;
//printf("Ans = %lld \n", Ans);
return;
} inline void update(Data &x, const int &a, const LL &v) {
//printf("insert v = %lld \n", v);
LL d1 = dis(x.a, a), d2 = dis(x.b, a), d3 = dis(x.a, x.b);
Ans = std::max(Ans, std::max(d1, d2) - v);
int xa = x.a, xb = x.b;
if(d1 > d3) {
x.b = a;
d3 = d1;
}
if(d2 > d3) {
x = Data(xb, a);
}
if(!x.a) x.a = a;
//printf("Ans = %lld \n", Ans);
return;
} void DFS_1(int x, int f) {
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS_1(y, x);
if(f) update(data[x], data[y], d[x] << );
//printf("data x : %d %d \n", data[x].a, data[x].b);
}
if(f) {
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
update(data[x], t, d[x] << );
}
}
return;
} inline void solve() { //printf("S2 inside \n"); for(int i = ; i <= n; i++) {
v[i].clear();
v[i].resize();
data[i].a = data[i].b = ;
}
Ans = -INF;
for(int i = ; i <= m; i++) {
int x = node[i].x, y = node[i].y, z = node[i].w;
if(x != z) {
fr[n + i * - ] = y;
d[n + i * - ] = d[y] + d[x] + node[i].val - node[i].z;
v[x].push_back(n + i * - );
//printf("%d : d = %lld fr = %d \n", n + i * 2 - 1, d[n + i * 2 - 1], fr[n + i * 2 - 1]);
}
if(y != z) {
fr[n + i * ] = x;
d[n + i * ] = d[x] + d[y] + node[i].val - node[i].z;
v[y].push_back(n + i * );
//printf("%d : d = %lld fr = %d \n", n + i * 2, d[n + i * 2], fr[n + i * 2]);
}
}
//puts("");
DFS_1(, ); if(Ans < (LL)-3e18) puts("F");
else printf("%lld\n", Ans >> );
return;
}
} inline void solve() {
scanf("%d", &n);
for(int i = ; i <= n; i++) {
fr[i] = i;
}
LL z;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
} DFS(, );
prework(); scanf("%d", &m);
bool S1 = true, S2 = true;
int lastLca = -;
for(int i = , x, y; i <= m; i++) {
scanf("%d%d%lld", &x, &y, &z);
node[i].x = x;
node[i].y = y;
node[i].z = z;
node[i].val = dis(x, y) - z;
int temp = lca(x, y);
if(lastLca == -) lastLca = temp;
else if(lastLca != temp) S2 = false;
if(visLca[temp]) S1 = false;
else visLca.set(temp);
node[i].w = temp;
} if(S1) {
Sone::solve();
return;
}
if(S2) {
Stwo::solve();
return;
} return;
} int main() { //freopen("in.in", "r", stdin);
//freopen("my.out", "w", stdout); for(int i = ; i < N; i++) pw[i] = pw[i >> ] + ; int T;
scanf("%d", &T);
while(T--) {
solve();
if(T) clear();
}
return ;
}
35分S1+S2代码
终于到正解了...考虑两条链如果有交,那么要么是直上直下的交,lca不同;要么是交了一段可能不直上直下的,lca相同。
那么lca不同的所有情况直接调用S1即可。lca相同的情况,可能在很多点相同。此时我们枚举每个点,把以这些点为lca的链都提出来建虚树,套用S2即可。
考虑为什么套用S1的时候不会把本来属于S2的情况算得更优。
注意到一个细节,就是S1中如果两个链加到线段树的同一下标上(lca相同),我们是不会把这两条链拿去更新答案的。于是S1中更新的就都是lca不同的啦!
#include <bits/stdc++.h> #define forson(x, i) for(int i = e[x]; i; i = edge[i].nex) typedef long long LL;
const int N = ;
const LL INF = 4e18; struct Edge {
int nex, v;
LL len;
}edge[N << ]; int tp = ; struct Node {
int x, y, w;
LL val, z;
}node[N]; struct Data {
int a, b;
Data(int A = , int B = ) : a(A), b(B) {}
}data[N]; int e[N], num2, pos2[N], ST[N][], pw[N], deep[N], n, m, fa[N], fr[N];
LL d[N], Ans; inline void add(int x, int y, LL z) {
tp++;
edge[tp].v = y;
edge[tp].len = z;
edge[tp].nex = e[x];
e[x] = tp;
return;
} inline void clear() {
memset(e + , , n * sizeof(int));
tp = ;
num2 = ;
return;
} void DFS(int x, int f) {
pos2[x] = ++num2;
ST[num2][] = x;
deep[x] = deep[f] + ;
fa[x] = f;
forson(x, i) {
int y = edge[i].v;
if(y == f) {
continue;
}
d[y] = d[x] + edge[i].len;
DFS(y, x);
ST[++num2][] = x;
}
return;
} inline void prework() {
for(int j = ; j <= pw[num2]; j++) {
for(int i = ; i + ( << j) - <= num2; i++) {
if(deep[ST[i][j - ]] < deep[ST[i + ( << (j - ))][j - ]]) {
ST[i][j] = ST[i][j - ];
}
else {
ST[i][j] = ST[i + ( << (j - ))][j - ];
}
}
}
return;
} inline int lca(int x, int y) {
x = pos2[fr[x]];
y = pos2[fr[y]];
if(x > y) std::swap(x, y);
int t = pw[y - x + ];
if(deep[ST[x][t]] < deep[ST[y - ( << t) + ][t]]) {
return ST[x][t];
}
else {
return ST[y - ( << t) + ][t];
}
} inline LL dis(int x, int y) {
if(!x || !y) return -INF;
return d[x] + d[y] - * d[lca(x, y)];
} inline bool cmp(const int &a, const int &b) {
return pos2[a] < pos2[b];
} namespace Sone { /// lca != lca
int rt[N];
std::vector<int> v[N];
namespace seg {
const int M = ; int ls[M], rs[M], tot;
LL large[M], largeD[M]; inline void pushup(int o) {
large[o] = std::max(large[ls[o]], large[rs[o]]);
largeD[o] = std::max(largeD[ls[o]], largeD[rs[o]]);
return;
}
void insert(int p, LL v, LL v2, LL v3, int l, int r, int &o) {
if(!o) {
o = ++tot;
ls[o] = rs[o] = ;
large[o] = largeD[o] = -INF;
}
if(l == r) {
large[o] = std::max(large[o], v);
largeD[o] = std::max(largeD[o], v + v2);
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
Ans = std::max(Ans, largeD[rs[o]] + v - v3);
insert(p, v, v2, v3, l, mid, ls[o]);
}
else {
Ans = std::max(Ans, large[ls[o]] + v + v2 - v3);
insert(p, v, v2, v3, mid + , r, rs[o]);
}
pushup(o);
return;
}
int merge(int x, int y, LL v) {
if(!x || !y) return x | y;
Ans = std::max(Ans, std::max(large[ls[x]] + largeD[rs[y]], large[ls[y]] + largeD[rs[x]]) - v);
large[x] = std::max(large[x], large[y]);
largeD[x] = std::max(largeD[x], largeD[y]);
ls[x] = merge(ls[x], ls[y], v);
rs[x] = merge(rs[x], rs[y], v);
return x;
}
void del(int p, int l, int r, int o) {
if(!o) {
return;
}
if(l == r) {
large[o] = largeD[o] = -INF;
return;
}
int mid = (l + r) >> ;
if(p <= mid) {
large[rs[o]] = largeD[rs[o]] = -INF;
del(p, l, mid, ls[o]);
}
else {
del(p, mid + , r, rs[o]);
}
pushup(o);
return;
}
} void DFS_1(int x, int f) {
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
seg::insert(deep[node[t].w], node[t].val, d[node[t].w], d[x], , n, rt[x]);
}
forson(x, i) {
int y = edge[i].v;
if(y == f) continue;
DFS_1(y, x);
seg::del(deep[x], , n, rt[y]);
rt[x] = seg::merge(rt[x], rt[y], d[x]);
}
return;
} inline void solve() {
seg::tot = ;
seg::large[] = seg::largeD[] = -INF;
memset(rt + , , n * sizeof(int));
for(int i = ; i <= n; i++) v[i].clear(); for(int i = ; i <= m; i++) {
int x = node[i].x, y = node[i].y, z = node[i].w;
if(x != z) {
v[x].push_back(i);
}
if(y != z) {
v[y].push_back(i);
}
} DFS_1(, );
return;
}
} namespace Stwo { /// lca = 1
Edge EDGE[N << ]; int TP;
int E[N], use[N], Time, cnt, imp[N], stk[N], top;
std::vector<int> v[N], vx[N]; inline void ADD(int x, int y) {
TP++;
EDGE[TP].v = y;
EDGE[TP].nex = E[x];
E[x] = TP;
return;
} inline void work(int x) {
if(use[x] != Time) {
use[x] = Time;
E[x] = ;
v[x].clear();
data[x].a = data[x].b = ;
}
return;
} inline void update(Data &x, const Data &y, const LL &v) {
LL d12 = dis(x.a, x.b), d34 = dis(y.a, y.b);
LL d13 = dis(x.a, y.a), d14 = dis(x.a, y.b);
LL d23 = dis(x.b, y.a), d24 = dis(x.b, y.b);
Ans = std::max(Ans, (std::max(std::max(d13, d14), std::max(d23, d24)) - v) >> );
int xa = x.a, xb = x.b;
if(d34 > d12) {
x = y;
d12 = d34;
}
if(d13 > d12) {
x = Data(xa, y.a);
d12 = d13;
}
if(d14 > d12) {
x = Data(xa, y.b);
d12 = d14;
}
if(d23 > d12) {
x = Data(xb, y.a);
d12 = d23;
}
if(d24 > d12) {
x = Data(xb, y.b);
}
if(!x.a) x = y;
return;
} inline void update(Data &x, const int &a, const LL &v) {
LL d1 = dis(x.a, a), d2 = dis(x.b, a), d3 = dis(x.a, x.b);
Ans = std::max(Ans, (std::max(d1, d2) - v) >> );
int xa = x.a, xb = x.b;
if(d1 > d3) {
x.b = a;
d3 = d1;
}
if(d2 > d3) {
x = Data(xb, a);
}
if(!x.a) x.a = a;
return;
} void dfs(int x, int f) {
for(int i = E[x]; i; i = EDGE[i].nex) {
int y = EDGE[i].v;
if(y == f) continue;
dfs(y, x);
if(f) update(data[x], data[y], d[x] << );
}
if(f) {
for(int i = ; i < (int)v[x].size(); i++) {
int t = v[x][i];
update(data[x], t, d[x] << );
}
}
return;
} inline void build_t() {
std::sort(imp + , imp + cnt + , cmp);
cnt = std::unique(imp + , imp + cnt + ) - imp - ; stk[top = ] = imp[];
for(int i = ; i <= cnt; i++) {
int x = imp[i], y = lca(x, stk[top]);
work(x); work(y);
while(top > && pos2[y] <= pos2[stk[top - ]]) {
ADD(stk[top - ], stk[top]);
top--;
}
if(y != stk[top]) {
ADD(y, stk[top]);
stk[top] = y;
}
stk[++top] = x;
}
while(top > ) {
ADD(stk[top - ], stk[top]);
top--;
}
return;
} inline void solve() { for(int i = ; i <= n; i++) {
vx[i].clear();
} for(int i = ; i <= m; i++) {
vx[node[i].w].push_back(i);
} for(int rt = ; rt <= n; rt++) {
if(!vx[rt].size()) continue;
++Time;
TP = cnt = ;
work(rt);
imp[++cnt] = rt;
for(int j = ; j < (int)vx[rt].size(); j++) {
int i = vx[rt][j];
int x = node[i].x, y = node[i].y, z = node[i].w;
work(x); work(y);
imp[++cnt] = x;
imp[++cnt] = y;
if(x != z) {
fr[n + i * - ] = y;
d[n + i * - ] = d[y] + d[x] + node[i].val - node[i].z;
v[x].push_back(n + i * - );
}
if(y != z) {
fr[n + i * ] = x;
d[n + i * ] = d[x] + d[y] + node[i].val - node[i].z;
v[y].push_back(n + i * );
}
}
build_t();
dfs(rt, );
}
return;
}
} inline void solve() {
Ans = -INF;
scanf("%d", &n);
for(int i = ; i <= n; i++) {
fr[i] = i;
}
LL z;
for(int i = , x, y; i < n; i++) {
scanf("%d%d%lld", &x, &y, &z);
add(x, y, z);
add(y, x, z);
} DFS(, );
prework(); scanf("%d", &m);
for(int i = , x, y; i <= m; i++) {
scanf("%d%d%lld", &x, &y, &z);
node[i].x = x;
node[i].y = y;
node[i].z = z;
node[i].val = dis(x, y) - z;
node[i].w = lca(x, y);
} Sone::solve();
Stwo::solve(); if(Ans < (LL)-1e18) puts("F");
else printf("%lld\n", Ans);
return;
} int main() { for(int i = ; i < N; i++) pw[i] = pw[i >> ] + ; int T;
scanf("%d", &T);
while(T--) {
solve();
if(T) clear();
}
return ;
}
AC代码
这什么鬼题啊...搞了4天,结果写完啥都没学到......
LOJ#2722 情报中心的更多相关文章
- BZOJ5419[Noi2018]情报中心——线段树合并+虚树+树形DP
题目链接: [NOI2018]情报中心 题目大意:给出一棵n个节点的树,边有非负边权,并给出m条链,对于每条链有一个代价,要求选出两条有公共边的链使两条链的并的边权和-两条链的代价和最大. 花了一天的 ...
- 微软威胁情报中心总经理的十句话——From John Lambert——太精辟了.......
微软威胁情报中心总经理 John Lambert的十句话 1. What is the most ...
- LOJ2722 「NOI2018」情报中心
「NOI2018」情报中心 题目描述 C 国和D 国近年来战火纷飞. 最近,C 国成功地渗透进入了D 国的一个城市.这个城市可以抽象成一张有$n$ 个节点,节点之间由$n - 1$ 条双向的边连接的无 ...
- luogu P4775 [NOI2018]情报中心 线段树合并 虚树 树的直径trick
LINK:情报中心 神题! 写了一下午 写到肚子疼. 调了一晚上 调到ex 用的是网上dalao的方法 跑的挺快的. 对于链的暴力 我不太会kk. 直接说正解吧: 分类讨论两种情况: 1 答案的两条链 ...
- 【LOJ】#2722. 「NOI2018」情报中心
https://loj.ac/problem/2722 题解 考场上想了60分,但是由于自己不知道在怎么zz,我连那个ai<bi都没看到,误以为出题人没给lca不相同的部分分,然后觉得lca不同 ...
- UOJ#397. 【NOI2018】情报中心 线段树合并 虚树
原文链接www.cnblogs.com/zhouzhendong/p/UOJ397.com 前言 这真可做吗?只能贺题解啊-- 题解 我们称一条路径的 LCA 为这条路径两端点的 LCA. 我们将相交 ...
- LOJ#2339 通道
题意:给你三棵树,求所有点对在三棵树上的距离和中的最大值. 解:首先有个暴力,然后还有个迭代乱搞,可以得到61分... namespace bf { inline void solve() { ; i ...
- LOJ#2553 暴力写挂
题意:给定两棵树T1,T2,求d1[x] + d1[y] - d1[lca1(x, y)] - d2[lca2(x, y)]的最大值. 解:考虑把上面这个毒瘤东西化一下.发现它就是T1中x,y到根的路 ...
- 【新业务搭建】竞争情报业务规划及体系构建的思考——By Team
竞争情报业务规划.体系构建 一.竞争情报业务定位——“做什么” 一)业务愿景.目标和原则 愿景:将情报工作融入到公司各个业务中,成为业务活动的灯塔 目标:直接支撑标杆学习(间接支撑三大战略).直接支持 ...
随机推荐
- hdu1421_搬寝室
题目:搬寝室 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1421 #include<stdio.h> #include<algor ...
- 剑指offer(4)
题目: 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树.假设输入的前序遍历和中序遍历的结果中都不含重复的数字.例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2 ...
- python爬虫之Beautiful Soup的基本使用
1.简介 简单来说,Beautiful Soup是python的一个库,最主要的功能是从网页抓取数据.官方解释如下: Beautiful Soup提供一些简单的.python式的函数用来处理导航.搜索 ...
- git的简单使用(一些小操作,持续更新)
第一次使用git的过程记录 参考了两个文章 菜鸟教程-git简明指南 阮一峰-常用git命令清单 git的几个工作区(此处参考了上面的两篇介绍) 简单步骤如下 git init 在当前目录建立工作区 ...
- java构造器和构建器
本文摘自:https://blog.csdn.net/wh2827991/article/details/79013115 在实例化一个类的过程中,通常会遇到多个参数的构造函数,但如果有些参数是非必需 ...
- Ajax与CORS通信
处理跨域的主要方法 JSONP CORS 本文主要讨论CORS解决Ajax因为浏览器同源策略不能跨域请求数据的问题. 1. JSONP JSONP跨域可以参考下面这篇博客 JSONP跨域 2. COR ...
- 红米Note 7 Pro在印度首销迅速售罄
3月13日消息,红米Note 7 Pro在印度率先发售. 小米印度业务负责人Manu Kumar Jain发推特表示,红米Note 7 Pro开售几秒钟就被抢光,我们的工厂正在加班加点工作,全力以赴提 ...
- linux下如何安装mysql和redis
linux下如何安装mysql(mariadb) linux下如何安装软件? 1. yum安装软件也得注意,一个是配置yum源 1.我们当前的是阿里云的yum源(下载速度特别快) 通过 yum ins ...
- VSCode里面HTML添加CSS时没有提示
看到知乎上的回答,vscode修改设置的: "editor.parameterHints": true, "editor.quickSuggestions": ...
- luogu P1353 【[USACO08JAN]跑步Running】
USACO!!! 唉!无一例外又是母牛(终于知道美国的牧场养什么了) 今天的主人公是一个叫贝茜的公主病母牛(好洋气) 可是她叫什么和我们理解题好像没有什么关系 通过读题我们可以发现她有三个傲娇的地方 ...
