有向无环图（DAG）的最小路径覆盖（转）

DAG的最小路径覆盖

定义：在一个有向图中，找出最少的路径，使得这些路径经过了所有的点。

最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖。

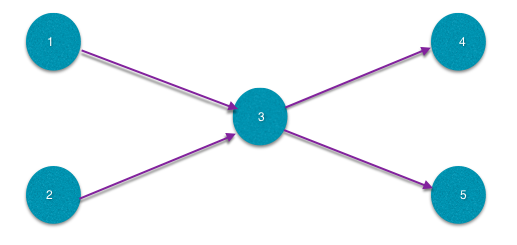
最小不相交路径覆盖：每一条路径经过的顶点各不相同。如图，其最小路径覆盖数为3。即1->3>4，2，5。

最小可相交路径覆盖：每一条路径经过的顶点可以相同。如果其最小路径覆盖数为2。即1->3->4，2->3>5。

特别的，每个点自己也可以称为是路径覆盖，只不过路径的长度是0。

DAG的最小不相交路径覆盖

算法：把原图的每个点V拆成VxVx和VyVy两个点，如果有一条有向边A->B，那么就加边Ax−>ByAx−>By。这样就得到了一个二分图。那么最小路径覆盖=原图的结点数-新图的最大匹配数。

证明：一开始每个点都是独立的为一条路径，总共有n条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径，也就相当于路径数减少了1。所以找到了几条匹配边，路径数就减少了多少。所以有最小路径覆盖=原图的结点数-新图的最大匹配数。

因为路径之间不能有公共点，所以加的边之间也不能有公共点，这就是匹配的定义。

习题：POJ1422

//
//  main.cpp
//  POJ1422最小不想交路径覆盖
//
//  Created by beMaster on 16/4/8.
//  Copyright © 2016年 beMaster. All rights reserved.
//

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int N =  + ;
vector<int> g[N];
int cy[N];
bool vis[N];
bool dfs(int u){
    for(int i=; i<g[u].size(); ++i){
        int v = g[u][i];
        if(vis[v]) continue;
        vis[v] = true;
        if(cy[v]==- || dfs(cy[v])){
            cy[v] = u;
            return true;
        }
    }
    return false;
}
int solve(int n){
    int ret = ;
    memset(cy, -, sizeof(cy));
    for(int i=;i<=n;++i){
        memset(vis, , sizeof(vis));
        ret += dfs(i);
    }
    return n - ret;
}
int main(int argc, const char * argv[]) {
    int t,n,m;
    int u,v;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;++i)
            g[i].clear();
        for(int i=;i<m;++i){
            scanf("%d%d",&u,&v);
            g[u].push_back(v);
        }

        int ans = solve(n);
        printf("%d\n",ans);
    }
    return ;
}

DAG的最小可相交路径覆盖

算法：先用floyd求出原图的传递闭包，即如果a到b有路径，那么就加边a->b。然后就转化成了最小不相交路径覆盖问题。

证明：为了连通两个点，某条路径可能经过其它路径的中间点。比如1->3->4，2->4->5。但是如果两个点a和b是连通的，只不过中间需要经过其它的点，那么可以在这两个点之间加边，那么a就可以直达b，不必经过中点的，那么就转化成了最小不相交路径覆盖。

题目：POJ2594

//
//  main.cpp
//  POJ2594最小可相交路径覆盖
//
//  Created by beMaster on 16/4/8.
//  Copyright © 2016年 beMaster. All rights reserved.
//

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int N =  + ;
bool dis[N][N];
bool vis[N];
int cy[N];
void floyd(int n){
    for(int i=;i<=n;++i)
        for(int j=;j<=n;++j)
            for(int k=;k<=n;++k)
                if(dis[i][k] && dis[k][j])//传递可达性
                    dis[i][j] = true;
}
bool dfs(int u, int n){
    for(int i=;i<=n;++i){
        if(!vis[i] && dis[u][i]){
            vis[i] = true;
            if(cy[i]==- || dfs(cy[i], n)){
                cy[i] = u;
                return true;
            }
        }
    }
    return false;
}
int solve(int n){
    int cnt = ;
    memset(cy,-,sizeof(cy));
    for(int i=;i<=n;++i){
        memset(vis,,sizeof(vis));
        cnt += dfs(i, n);
    }
    return n - cnt;
}
int main(int argc, const char * argv[]) {
    int n,m;
    int a,b;
    while(scanf("%d%d",&n,&m),n+m){
        for(int i=;i<=n;++i)
            for(int j=;j<=n;++j)
                dis[i][j] = false;
        for(int i=;i<=m;++i){
            scanf("%d%d",&a,&b);
            dis[a][b] = true;
        }
        floyd(n);
        int ans = solve(n);
        printf("%d\n",ans);
    }
    return ;
}