poj1375Intervals(点到圆的切线）

链接

貌似这样的叫解析几何

重点如何求得过光源到圆的切线与地板的交点x坐标，可以通过角度及距离来算，如图，

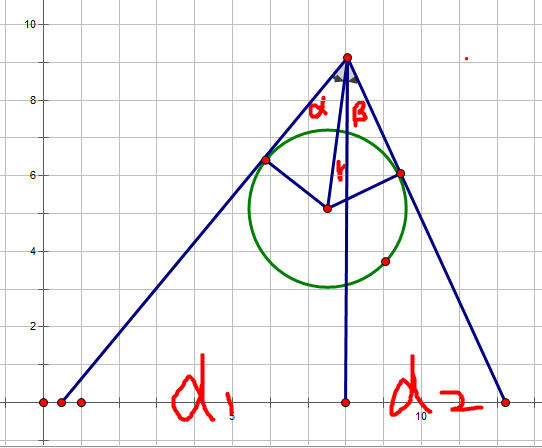
根据距离和半径可以求得角度a、b、r,自然也可以求得d1,d2.

至于方向问题，在求r得时候 可以使r = asin(（p.x-c.x）/d） p为源点，c为圆心 ，d为两点距离。

若在反方向，自然r为负角 ，并不影响最后的结果。

排序后，统计区间就可以了。

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 505
 #define LL long long
 #define INF 0xfffffff
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 struct point
 {
     double x,y;
     double r;
     point(double x=,double y=):x(x),y(y){}
 }p[N];
 struct node
 {
     double l,r;
 }li[N],ans[N];
 typedef point pointt;
 pointt operator -(point a,point b)
 {
     return point(a.x-b.x,a.y-b.y);
 }
 double dis(point a)
 {
     return sqrt(a.x*a.x+a.y*a.y);
 }
 node cal(point a,point b)
 {
     double ang1,ang2,ang3,ang4;
     double d = dis(a-b);
     ang1 = asin(a.r/d);
     ang2 = asin((b.x-a.x)/d);
     ang3 = ang1+ang2;
     ang4 = ang2-ang1;
     //cout<<ang1<<" "<<ang2<<" "<<ang3<<" "<<ang4<<endl;
     node ll;
     double l = b.x-b.y*tan(ang3);
     double r = b.x-b.y*tan(ang4);
     ll.l = min(l,r);
     ll.r = max(l,r);
     return ll;
 }
 bool cmp(node a,node b)
 {
     return a.l<b.l;
 }
 int main()
 {
     int n,i;
     point pp;
     while(scanf("%d",&n)&&n)
     {
         scanf("%lf%lf",&pp.x,&pp.y);
         for(i = ; i <= n; i++)
         scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].r);
         for(i = ; i <= n; i++)
         {
             li[i] = cal(p[i],pp);
         }
         sort(li+,li+n+,cmp);
         int g = ;
         ans[g].l = li[].l;
         double te = li[].r;
         for(i =  ; i <= n; i++)
         {
             if(li[i].l>te)
             {
                 ans[g].r = te;
                 ans[++g].l = li[i].l;
             }
             te = max(te,li[i].r);
         }
         ans[g].r = te;
         for(i = ; i <= g; i++)
         printf("%.2f %.2f\n",ans[i].l,ans[i].r);
         puts("");
     }
     return ;
 }