OpenFOAM——具有压差且平行平板间具有相对运动流动

本算例翻译整理自：http://the-foam-house5.webnode.es/products/chapter-1-plane-parallel-plates-case/

这个算例中两平板间具有相对运动，并且沿x方向存在压力梯度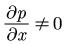（）。针对这个计算，轴线位于两板中间。

连续性方程：

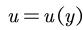
简化x方向的动量方程：

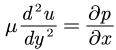
在这个算例中，压力梯度必须被考虑。此外，v=w=0并且根据y轴和z轴的动量方程：

这是具有压力梯度的库埃特流的通解：非对称抛物线的速度分布

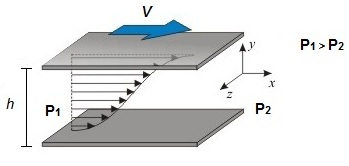
对于OpenFOAM的求解，给定h的值为0.1m，平板的长度设定为2m，移动壁面的水平速度V=10m/s，将通过在出口处施加真空而保持入口处的环境压力而形成压力梯度（P₁=101325Pa和P₂=0Pa）。顶部的壁面速度从1m/s更改为10m/s以后，可以更好的观察到两种边界条件的共同影响。

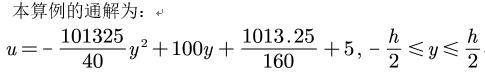
我们利用上次《平行平板间具有相对运动（库埃特流）》的算例新建本次的算例，使用下面的命令在原有算例的基础上新建算例：

foamCloneCase ./plate_two ./plate_combine

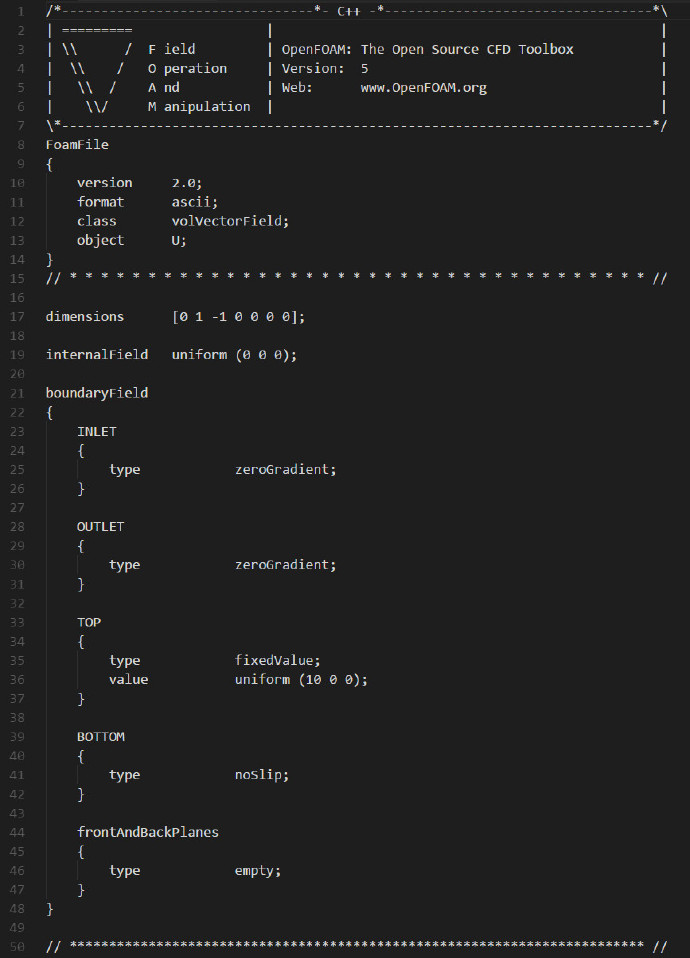
我们只需要修改新算例下0文件夹的U文件，system目录下的controlDict文件，其他保持不变

U文件当中的内容如下：

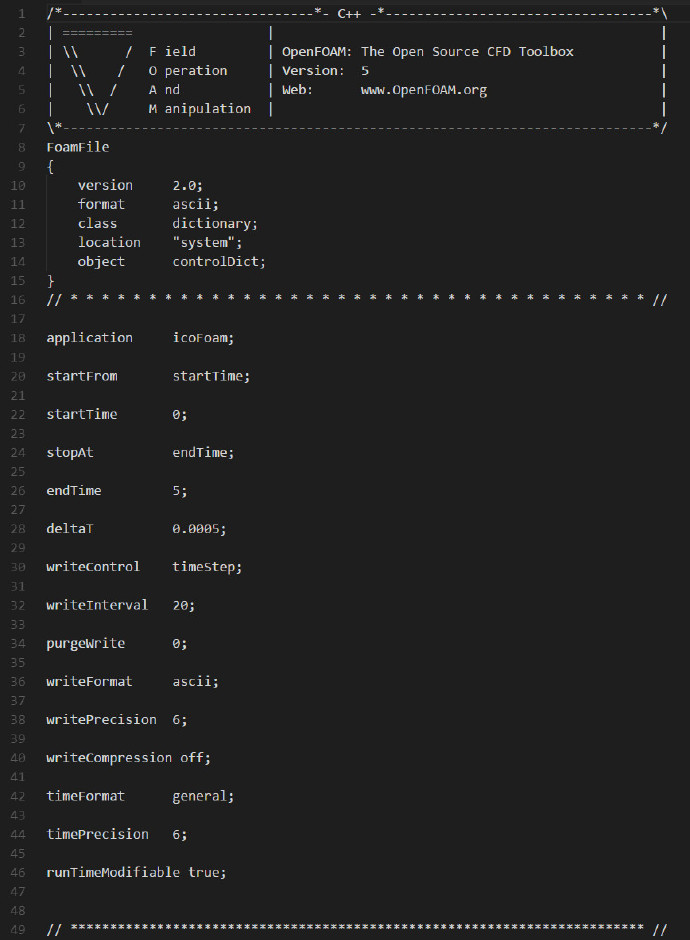
最后我们设置controlDict文件，我们为了保证库朗数小于1，我们只修改时间步长，设置为0.0005，其他的我们保持默认不变

设置好以后，进入算例目录，输入icoFoam开始计算：

等到计算结束

将计算结果导入paraview里面进行处理

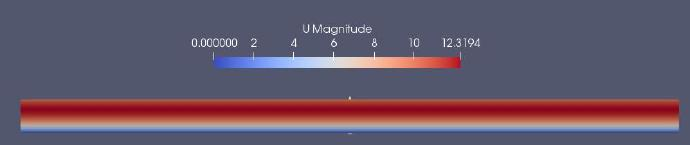
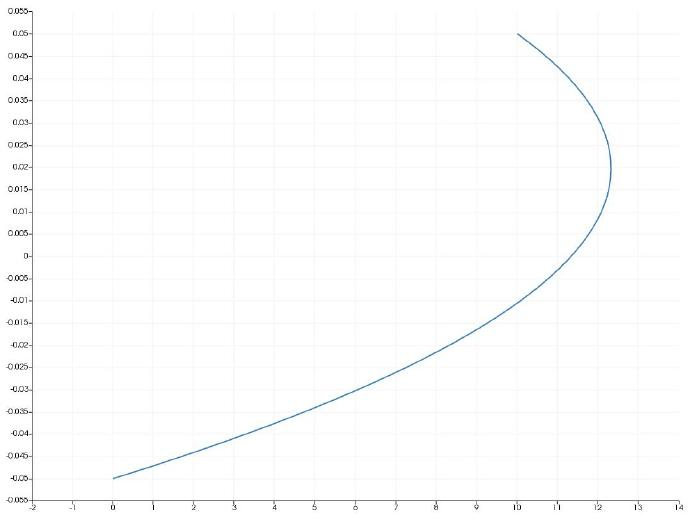
沿竖直方向的速度分布

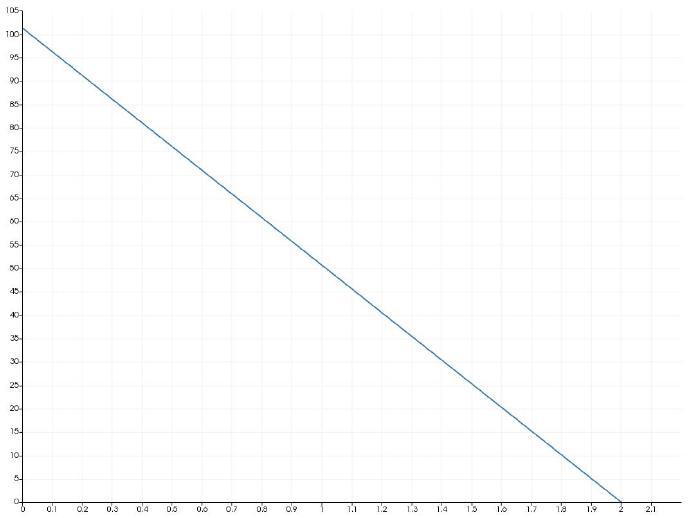
x方向压力分布：

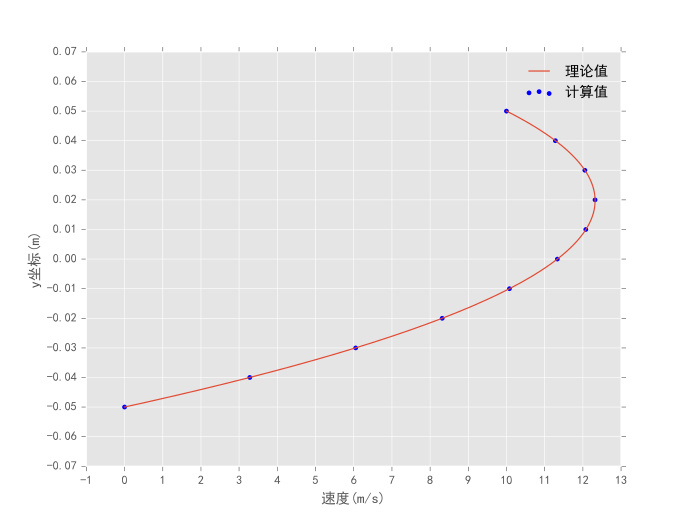
可以看出，解析解和数值结果是一致的