高斯混合模型（GMM）及MATLAB代码

之前在学习中遇到高斯混合模型，卡了很长一段时间，在这里记下学习中的一些问题以及解决的方法。希望看到这篇文章的同学们对高斯混合模型能有一些基本的概念。全文不废话，直接上重点。

本文将从以下三个问题详解高斯混合模型：

1.什么是高斯混合模型？

2.高斯混合模型的数学原理？

3.高斯混合模型在MATLAB中如何使用？

一、什么是高斯混合模型？

高斯混合模型，英文全称：Gaussian mixture model，简称GMM。高斯混合模型就是用高斯概率密度函数（二维时也称为：正态分布曲线）精确的量化事物，将一个事物分解为若干基于高斯概率密度函数行程的模型。这句话看起来有些深奥，这样去理解，事物的数学表现形式就是曲线，其意思就是任何一个曲线，无论多么复杂，我们都可以用若干个高斯曲线来无限逼近它，这就是高斯混合模型的基本思想。那么下图（图1.1）表示的就是这样的一个思想。

图1.1 任意曲线用高斯函数逼近

题外话：又由于高斯函数只要在样本数据点足够大时，可以表征任何一种事物的规律。在信号处理中常用高斯函数来代替冲击函数，用冲击函数的组合重构原始信号。所以用GMM表达任何曲线是可行的。（可能你不知道我这段话在说什么，没关系，这里只是用一个信号重构的实例来说明GMM的可行性）

好，我们继续，对于图1.1，换一种方式理解，曲线是模拟一组数据的结果，而这些数据分布情况如图1.2所示。那么此时GMM模拟出的曲线就有了现实的意义，这时就可以用构造好的GMM模型来表达这些数据，相比于存储数据，使用GMM中的参数来表达数据要方便简单的多，并且是数学上有完整的表达式。

图1.2  数据分布情况

反过来思考，假如先拿到的是图1.2，知道了数据的分布情况。如何用曲线和数学表达式来逼近模拟它呢？答：用高斯混合模型来做，做出来的结果如图1.1所示，图1.1中上方的曲线是由若干个高斯函数叠加而成的。以上就是高斯混合模型的基本概念。

增加数据维度，得到更为复杂一点的结果如图1.3所示，这也是我们经常看到GMM情况。

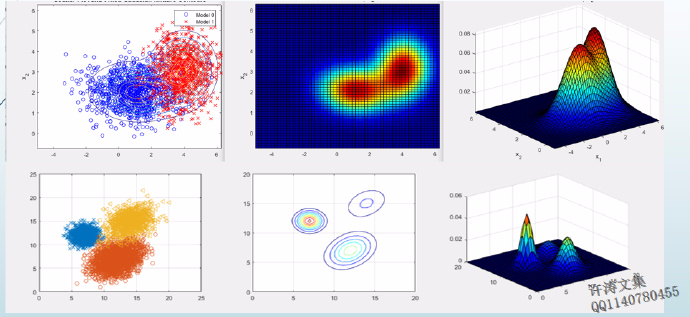图1.3 高斯混合模型拟合结果

题外话：高斯混合模型也被视为一种聚类方法，是机器学习中对“无标签数据”进行训练得到的分类结果。其分类结果由概率表示，概率大者，则认为属于这一类。

二、高斯混合模型的数学原理

在二维的情况下，理解起来很简单，如图1.1表示的那样，一个复杂的曲线可以用若干个组合起来的高斯函数来逼近。

在三维的情况下，同样的理解：任何一个曲面都可以用高斯函数来逼近。

在N维的情况下，任何一个模型都可以用高斯函数来逼近。（当然，这里用到的“高斯函数”的维度是跟着数据的变化而变化的）。好，这里重新复习了一下GMM的概念。数学原理我们从最简单的二维开始来理解，由浅入深。

2.1 二维高斯函数

二维高斯函数的表达式、图形以及似然估计中的3sigma原则，都在图中列出，码字不易，PPT也是自己做的，为了保护版权，添加了水印，如有疑问，可以联系图中QQ在线交流。

图2.1 二维高斯函数

2.2 三维高斯函数

三维高斯函数函数的数学表达式以及其中字母代表的含义，在图2.2中给出。

图2.2 三维高斯函数

由图2.2中的公式，进行绘图，得到如图2.3所示的结果。

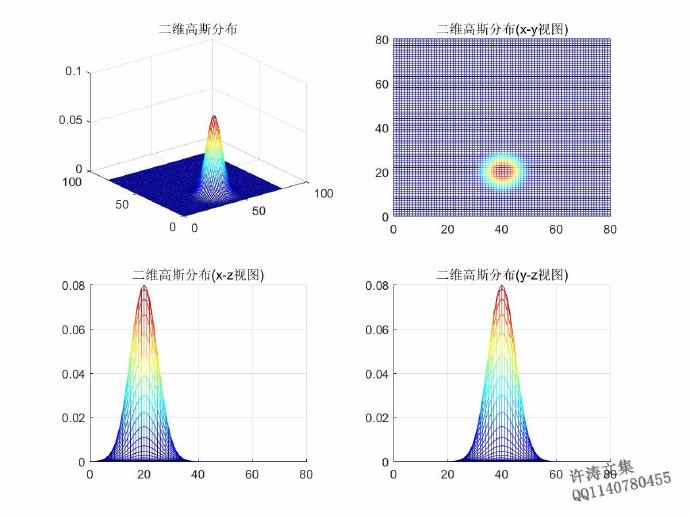图2.3 三维高斯函数绘图结果

（对于图2.3，解释一下，当时理解上出了一点小问题，把图中的二维都视为三维就好了，不影响。）

这里对图2.2和图2.3进行说明，u1和u2是均值，均值u的物理意义就是高斯混合模型的中心，这个中心可以表示为（u1,u2），标准差sigma决定高斯函数的形状，这和二维情况是一样的。在图2.3中下方两个图可以看到，从某一个二维坐标系来看，三维高斯函数可以简化为二维高斯函数。协方差rou表示的是数据的相关性。

2.3 N维高斯函数

N维高斯函数数学表达式由图2.4给出，其协方差的概念由图2.5给出。

图2.4 N为高斯函数

图2.5 N维高斯函数协方差

理解了三维高斯函数中各个参数的物理意义，在N维上面理解起来也就简单了。对于N维高斯函数，其数据的维度也是N维的，此时均值向量u是由N个均值u1,u2,...un组成的，其物理意义仍然是高斯函数的中心，协方差矩阵大sigma依旧表示的是高斯函数的形状，此时的大sigma是N行N列的矩阵，是如图2.5所示的由各个数据的协方差组成的矩阵。

好了，终于了解完一般高斯函数的形式，接下来要进入正题GMM了。

2.4 高斯混合模型的数学原理

前面我们首先了解了高斯混合模型是什么：用高斯函数近似表示曲线或者曲面。然后铺垫了部分数学基础：从二维到N维高斯函数的表达式及其参数的物理意义。下面由图2.6给出高斯混合模型的数学表达式

图2.6 高斯混合模型表达式

看到这个表达式是不是很高兴，没有想象中那么难，很简单的一行。这里说明一下：

（1）X是随机变量，可以理解为维度不定向量，X的维度决定了g(x)的维度，g(x)是单一高斯函数，也就是N维的高斯函数，其中N可以为任意整数，N由X的维度决定。

（2）回到之前的那个问题，用若干个高斯函数近似一个曲线或者曲面，无论这个曲线或者曲面是简单或复杂。要想实现近似，需要确定用多少个高斯函数来近似，这个高斯函数的个数用K表示，K的意义就是：GMM中单一高斯函数的个数。再专业一点，称K为GMM中成分的个数，其中成分指的就是单一高斯函数。【成分这个词在GMM中的由来是因为MATLAB中将GMM中高斯函数个数用“ComponentProportion”来表示，译为“成分”】

（3）混合权重中：每个单一高斯函数在GMM中所起的作用是不一样的，混合权重在决定了单一高斯函数在GMM中起的作用，可以联想本文中图1.1，拟合这条曲线的每个高斯函数的高度都是不一样的。

（4）维度的问题，这个比较好理解。维度就是随机变量X的维度，也就是单一高斯函数g(x)的维度，主要是由随机变量X的维度决定的。当一个高斯混合模型维数为N、成分为K时，我们称之为：K个成分N阶的高斯混合模型。

了解了以上概念之后，要确定一个高斯混合混合模型，要怎么做呢？关键是确定图2.6中的参数，如何确定？这里要用到EM算法【EM算法，指的是最大期望算法（Expectation Maximization Algorithm，又译期望最大化算法），是一种迭代算法，在统计学中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。】

三、高斯混合模型在MATLAB中的使用

在较新的MATLAB版本中，我用的是MATLAB2015A，此版本将关于高斯混合模型内容都集中在一个叫做：gmdistribution的类中。可以在MATLAB中输入：help gmdistribution，查看这个类的详细介绍和帮助文档。下面是对这个类简单的介绍。

gmdistribution类的介绍：

gmdistribution对象存储高斯混合分布, 也称为高斯混合模型 (GMM), 它是由多元高斯分布分量组成的多变量分布。每个分量由其平均值和协方差定义, 混合物由混合比例向量定义。

创造：可以通过两种方式创建gmdistribution模型对象。使用gmdistribution函数 (此处描述) 通过指定分布参数来创建gmdistribution模型对象。使用 fitgmdist 函数可以将gmdistribution模型对象与给定固定数量的组件的数据相匹配。

使用方法：

gm = gmdistribution(mu,sigma)

gm = gmdistribution(mu,sigma,p)

例子：gm = gmdistribution(mu,sigma) 创建一个gmdistribution模型对象使用指定的手段mu和方差sigma以相等的混合的比例。

gm = gmdistribution(mu,sigma,p) 指定多变量高斯分布分量的混合比例。

以上是使用指定的均值和方差构造高斯混合模型类，也就是根据给定的参数得到数据。然而我们常用的是根据数据的分布求得这些参数：均值、协方差、混合权重等，这时就要用到上文提到的fitgmdist函数了。【fitgmdist函数，只有在最新版本里才这么用，之前的版本称为：gmdistribution.fit，当然其在MATLAB里调用方式也不一样】

在MATLAB中输入：hlep gmdistribution，或者输入：help fitgmdist函数可以查看此函数的帮助文档，并且帮助文档中会给出部分例子。下面为对这个函数的介绍：

gmdistribution.fit（高斯混合参数估计）

注意

fit将被删除在未来的版本。改用 fitgmdist。（MATLAB的帮助文档很温馨，特意指出了这个函数在未来的版本可能会被删除，并且给出了修改使用的建议）

语法

obj= gmdistribution.fit(X,k)obj=gmdistribution.fit(...,param1,val1,param2,val2,...)

描述

obj = gmdistribution.fit(X,k) 使用期望最大化 (EM) 算法构造包含最大似然的 gmdistribution 类的对象obj高斯混合模型中的参数的估计与k分量的数据在n-m矩阵X, 其中n是观察的数量和m是数据的维度。gmdistribution将NaN值视为缺少的数据。包含NaN值的X行被排除在合适的范围内。

obj = gmdistribution.fit(...,param1,val1,param2,val2,...) 提供对迭代 EM 算法的控制。由于博客排版会乱，下面截图表示，图3.1为gmdistribution.fit函数的参数及其意义。看不清没关系，可以在MATLAB帮助文档里查找到。

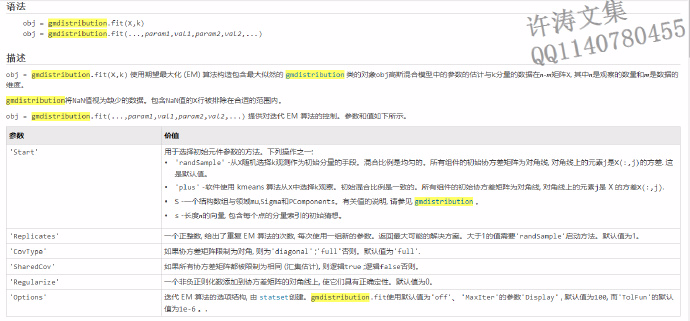图3.1 gmdistribution.fit函数参数意义

在某些情况下, gmdistribution可能收敛到一个或多个元件具有病态或奇异协方差矩阵的解。

下面的问题可能导致病态的协方差矩阵:

（1）数据的维数相对较高, 没有足够的观测。

（2）数据的某些功能 (变量) 是高度相关的。

（3）部分或全部功能是离散的。

（4）您试图将数据与太多组件相匹配。

通常, 通过使用下列预防措施之一, 可以避免获得病态的协方差矩阵:

（1）预处理数据以删除相关功能。

（2）将'SharedCov'设置为true可对每个组件使用相等的协方差矩阵。

（3）将'CovType' " 设置为'diagonal'.

（4）使用'Regularize'将一个非常小的正数添加到每个协方差矩阵的对角线上。

（5）请尝试另一组初始值。

在其他情况下, gmdistribution可能通过中间步骤, 其中一个或多个组件具有病态的协方差矩阵。尝试另一组初始值可能会避免此问题, 而不会更改数据或模型。

仔细看的话，会发现MATLAB帮助文档真的很给力，不仅给出了一系列的温馨提示，而且预知了一些在使用会遇到的问题以及如何去解决。比如上面给出导致协方差矩阵病态的原因以及怎么预防。

当然，使用新版本的我们要使用的函数是fitgmdist。来看一下这个函数：

fitgmdist（拟合高斯混合模型数据）

语法

GMModel = fitgmdist(X,k)

GMModel = fitgmdist(X,k,Name,Value)

描述

例子

GMModel = fitgmdist(X,k) 返回一个高斯混合分布模型 (GMModel), 其中k个成分适合数据 (X).

例子

GMModel = fitgmdist(X,k,Name,Value) 返回一个具有指定附加选项的高斯混合分布模型由一个或多个Name,Value对参数。例如, 可以指定正则值或协方差类型。

这里注意：虽然给出了两种函数，但是其使用方法都是一样的。使用起来也很简单，给出了两种调用方式，一种是简单的只要给定输入的随机变量，成分个数。另一种是可以指定具体参数如：协方差矩阵是否为对角等。

我们来运行一下MATLAB帮助文档给出的例子，看一看得到的结果里是什么情况。例子如图3.2所示，是MATLAB帮助文档给出的一个简单使用。

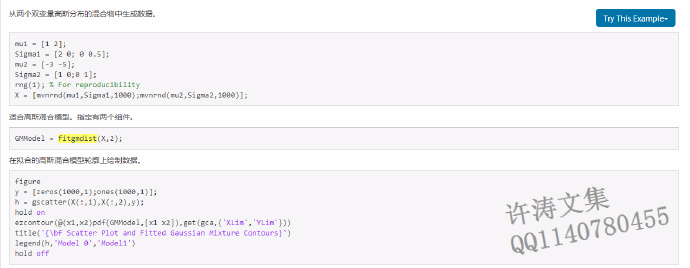图3.2 fitgmdist使用例子

图可能看不清，代码再次列出（代码换了一种颜色，以免混淆）：

mu1 = [1 2];

Sigma1 = [2 0; 0 0.5];

mu2 = [-3 -5];

Sigma2 = [1 0;0 1];

rng(1); % For reproducibility

X = [mvnrnd(mu1,Sigma1,1000);mvnrnd(mu2,Sigma2,1000)];

%适合高斯混合模型。指定有两个组件。

GMModel = fitgmdist(X,2);

%在拟合的高斯混合模型轮廓上绘制数据。

figure

y = [zeros(1000,1);ones(1000,1)];

h = gscatter(X(:,1),X(:,2),y);

hold on

ezcontour(@(x1,x2)pdf(GMModel,[x1 x2]),get(gca,{'XLim','YLim'}))

title('{\bf Scatter Plot and Fitted Gaussian Mixture Contours}')

legend(h,'Model 0','Model1')

hold off

将以上这段代码复制到MATLAB中运行，我们就成功使用了一次高斯混合模型，那么得到的结果图是什么意思呢。先来看下结果图3.3

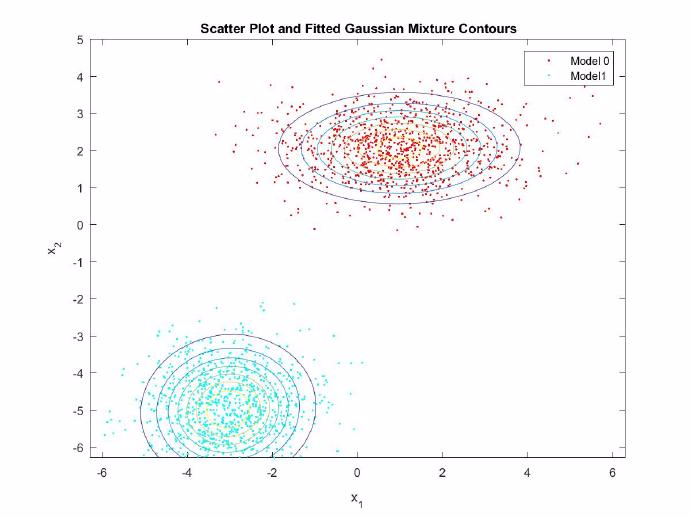图3.3 GMM例子结果图

这个图的表达的是，有两堆数据，可以用2个成分的高斯混合模型来描述。当然也可以用3个成分的或者4个成分或者任意自己想用的成分来描述，这里可以自己尝试，只要修改fitgmdist(X,K)中K的值就可以了。结果图是得到了，那么拟合后我们得到了什么呢？由于程序中这一句GMModel = fitgmdist(X,2);把结果存在GMModel变量中，可以在MATLAB工作区中查看GMModel。查看GMModel中的内容见图3.4。

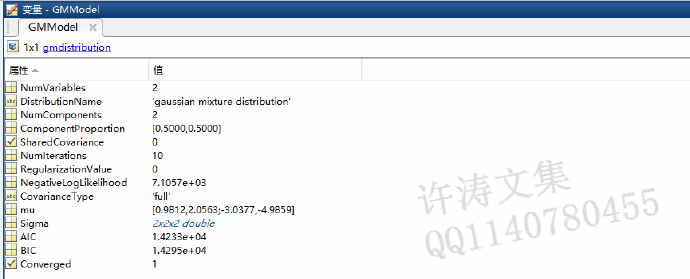图3.4 GMModel中的内容

由图可知，GMModel是gmdistribution类的一个数据，其中包含了许多类成员：如成分个数、分部名称、均值向量、协方差矩阵、协方差矩阵类型、是否正则化等等，具体列出关于确定这个高斯混合模型的所有参数以及参数的内容。

看到这里，恭喜你终于看完了高斯混合模型，是否对高斯混合模型有了初步的概念呢，如果还没有的话，可以把文档多看几遍、里面的代码自己敲一敲、函数的帮助文档自己查看一番。如果还有疑问，可以加图片水印中的QQ与我交流。【由于博文访问量变大，QQ消息也越来越多，有疑问的小伙伴可以整理好问题，发到我的邮箱：1140780455@qq.com，我看到后会逐一回复。】

一个例子回顾总结高斯混合模型

最后，用一个例子回顾并且总结一下高斯混合模型：

米饭的例子

最后用一个例子来总结一下我们今天一起学习的高斯混合模型，这个例子是我在食堂吃饭的时候突然想起的。

假如现在在食堂吃饭，找了张桌子，我打了一碗饭，往这里一坐，碗放在桌上。以俯视的角度从上往下看，此时把桌子看做坐标轴，米饭为数据点，这是在二维平面上，那么数据点是由二维坐标确定的。那么碗就可以看做GMM模型二维聚类俯视图的圈，聚类的中心点自然就是在碗里。此时的桌子、碗、米饭组成的整体，就可以称之为二维平面上的一成分高斯混合模型。

这个时候，突然来了个同学，也正好端着一碗米饭，在我对面坐下了，也把碗往桌上这么一放。此时平面上就有两堆数据点了，这就可以看做是两个成分的高斯混合模型。此时的桌子、碗、米饭组成的整体，就可以称之为二维平面上的二成分高斯混合模型。如果这个时候，我发现桌上有一粒米饭，我就想啊，这粒米饭到时是你碗里的呢，还是我碗里的呢，诶，这时就需要用到高斯混合模型估计了。步骤如下：1.根据两堆数据点确定高斯混合模型的参数均值向量和协方差矩阵，确定参数可以使用EM期望最大算法；这里最终得到描述两碗米饭的两个GMM。2.将桌上的这粒米饭以二维坐标表示，输入到我们计算好的两个高斯混合模型。得出在每个GMM下概率，一般情况下，哪个概率大，就认为属于哪一堆数据。一般的看来，会认为，这里米饭离谁近就是谁的，没错确实是这样。但是也有这样的可能，米饭是离我比较近，但是我打的是三毛的米饭，而你打的是两块的米饭，我的少，你的多，这个时候就不一定了，那么这就关系到GMM权重的设置了。

同样的，把食堂看做一个平面，把一个桌子上的碗装着的米饭，看做一堆数据。假设食堂有N张桌子，那么就有N堆数据，这时如果地上有一粒米饭，就需要对这N堆数据建模，然后根据此米饭的坐标确定大概是属于哪张桌子掉下来的。那么此时的模型就成为二维N成分高斯混合模型。

类似的，假设描述每粒米饭的参数不止是2个信息，还有其他像重量啊、米饭多长、多宽等N个参数，那么再来对刚刚讲的数据进行建模，此时就是N维空间中N个成分的高斯混合模型了。

以上我们假设碗是圆的，也就是高斯模型的协方差矩阵是对角化后的；假设用的是椭圆的盘子，椭圆时盘子不同的摆法就不一样了，情况复杂很多，此时就是协方差矩阵没对角化的情况。为什么呢，之前介绍过，因为任何一个非奇异矩阵，都可以对他进行分解，分解为一个对角阵乘以一个一般矩阵，这就是矩阵的奇异值分解，此时这个一般矩阵又可以称为旋转因子，因为图像的旋转几何运算都可以用矩阵的乘法来表示，换句话说，一副二维平面上的图像乘以一个矩阵，可以看做是把这个图形进行旋转了，最大奇异值对应的右特征向量是偏离原点最历害的方向。这只是针对这一种情况，当然还有平移因子，缩放因子等等，不同的变换因子矩阵形式是不一样的。

最后的最后，总结一下本篇博文遗留下来的问题：

1.高斯混合模型是否为全局最优？

2.如果数据不充分高斯混合模型的使用意义在哪？

3.面对维数灾难时，高斯混合模型该何去何从？

这些问题我也还没有弄清楚，欢迎大家一起讨论。

---摘自《许涛文集 学习笔记》

来源： http://blog.sina.com.cn/s/blog_a36a563e0102y2ec.html