Linear Discriminant Analysis Algorithm

线性判别分析算法。

逻辑回归是一种分类算法，传统上仅限于两类分类问题。

如果有两个以上的类，那么线性判别分析算法是首选的线性分类技术。LDA的表示非常直接。它包括数据的统计属性，为每个类计算。对于单个输入变量，这包括:

• 每个类的平均值。
• 在所有类中计算的方差。

通过计算每个类的判别值并对具有最大值的类进行预测，可以做出预测。

                                  

基本计算方法：

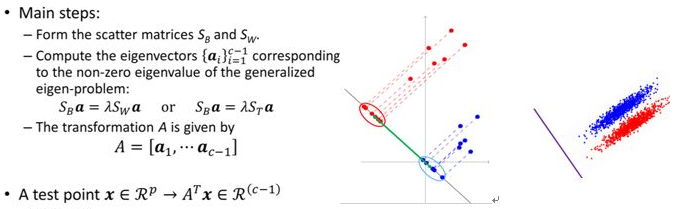
该方法假定数据具有高斯分布(钟形曲线)，因此，最好先从数据中删除异常值。这是一种简单而强大的分类预测建模问题的方法。

判别分析的典型例子是线性判别分析(Linear discriminant analysis)，简称LDA。（这里注意不要和隐含狄利克雷分布(Latent Dirichlet allocation)弄混，虽然都叫LDA但说的不是一件事。）

LDA的核心思想是把高维的样本投射(project)到低维上，如果要分成两类，就投射到一维。要分三类就投射到二维平面上。这样的投射当然有很多种不同的方式，LDA投射的标准就是让同类的样本尽量靠近，而不同类的尽量分开。对于未来要预测的样本，用同样的方式投射之后就可以轻易地分辨类别了。

使用情景：

• 判别分析适用于高维数据需要降维的情况，自带降维功能使得我们能方便地观察样本分布。它的正确性有数学公式可以证明，所以同样是很经得住推敲的方式。
• 但是它的分类准确率往往不是很高，所以不是统计系的人就把它作为降维工具用吧。
• 同时注意它是假定样本成正态分布的，所以那种同心圆形的数据就不要尝试了。

更多可以参考：https://www.cnblogs.com/pinard/p/6244265.html