SIGAI机器学习第二十三集 高斯混合模型与EM算法

讲授高斯混合模型的基本概念，训练算法面临的问题，EM算法的核心思想，算法的实现，实际应用。

大纲：

高斯混合模型简介
实际例子
训练算法面临的困难
EM算法
应用-视频背景建模
总结

高斯混合模型简写GMM，期望最大化算法EM。概率分布要确定里边的参数有两种手段，即据估计、最大似然估计。

高斯混合模型简介：

高斯分布也叫正态分布，在机器学习的一些书和论文里边，一般把它称为高斯分布，尤其是老外习惯这样写。

高斯混合模型是多个高斯分布的一个叠加，它的概率密度函数可以写成：

其中x肯定是一个连续性的随机变量，一般x∈Rⁿ，每一个Ni()都是Rⁿ的正态分布，即N维空间的一个正态分布（多元正态分布），需要注意的是高斯分布权重之和wi加起来要等于1（为什么要加起来等于1呢？因为一个函数要是能充当概率密度函数它有两个要求，p(x)≥0和实数范围积分为1），所以对上边式子积分，必然得到Ni()积分为1，所以wi之和也为1。

高斯混合模型它就是多个高斯分布的叠加，就像信号处理里边的任何一个信号可以看成多个各种频率和相位的正弦波的叠加，傅里叶变换和傅里叶级数就是干这样的一个事情的。可以给高斯混合模型一个很直观的解释，任意一个样本可以看作是先从 个高斯分布中选择出一个，选择第 个高斯分布的概率为 ，再由这个个高斯分布产生出样本数据x，对应的权重为wi。

高斯混合模型可以逼近任何一个连续的概率分布，任何一个连续性的随机变量我们都可以用高斯混合模型去拟合它，因此它可以看做是连续性概率分布的万能逼近器。前边神经网络它有万能逼近定理，它可以拟合任何一个连续函数。高等数学中，用三角级数或者用多项式的函数可以来逼近任何一个连续函数。这都是类似的道理，这里是用高斯分布来逼近任何一个连续的分布。如果你有一个概率密度函数不知道长什么样子，采了一组样本的话，你完全可以用高斯分布去拟合它，达到任何一个指定的精度。

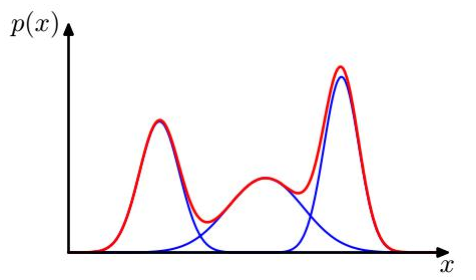
x是一维向量，它的概率密度函数可以看成是三个高斯分量的叠加，高斯分布方差越大图像越宽。

实际例子：

肤色建模：

不同人种的皮肤颜色差异很大，如果是彩色图像，在RGB空间中肤色会聚集成多个团，此时用高斯混合模型来表示是非常合适的。
可能有白人、黄人、黑人，他人服从的分布肯定是不一样的，三维空间中分布在不同的地方呈现不同的三维正态分布。

训练算法面临的困难：

前边说了高斯混合模型的定义以及实际的例子，接下来就要解决一个核心的问题，   高斯混合模型它的参数是怎么得到的，和其他一些机器学习算法一样，或者说和其他一些参数估计方法像概率统计中最大似然估计估计概率密度函数的参数其实他也是一种机器学习的算法，它是通过训练样本得到的，通过一组训练样本，把它的均值和协方差估计出来，比如说正态分布而言，这里高斯分布模型在正态分布的基础之上又多了一组东西，除了有k组分量（均值和方差）外多了一组权重wi，训练算法要同时确定k个分量的权重、协方差、均值，这里k是人工指定的不需要算法来自动确定。接下来看算法是怎么做的。

这里要通过最大似然估计来确定它的参数，最大似然估计是，给定一组训练样本xi,i=1,2...,l，先构造一个对数似然函数，然后去最大化它，可以估计出均值和协方差，对数似然函数就是在似然函数的基础之上取了一个对数而已，连乘变成连加的形式，当然这些样本是独立同分布的，那么最后要求解的就是下边这样的一个最大化问题：

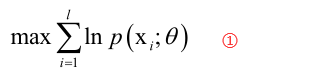
其中θ是我们要确定的参数，如均值和方差。对于高斯混合模型套用上边的公式变为：

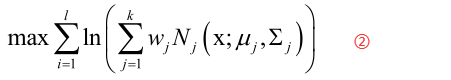
对于任意一个连续性的分布我们都可以用最大似然估计把参数给确定出来，比如说对于正态分布通过求似然函数①式的极值，其实就是对协方差矩阵Σ和均值向量μ求偏导数然后等于0最后把它接出来，那么就套用这个方法，用②式对所有的参数wj、μj、Σj求偏导令其等于0然后解方程，但是最后式借不出来的，核心的问题是②式中多了一个求和项，这样直接算的话是不能算出他的一个精确解。问题是多了一个权重系数wj，假设我们知道所有的样本的每一个样本服从什么分布，假设这个高斯混合模型它有三个高斯分布N1、N2、N3，假设我们有100个训练样本，我们知道1-30个样本属于第一个高斯分布、31-60个样本是属于第二个高斯分布的，61-100个样本是属于第三个高斯分布的，那么这个问题也可以解决，就用1-30个样本来训练第一个高斯分量，可以用最大似然估计把它的μ和Σ给算出来，同样的用各自的样本把各自分布的μ和Σ给算出来，但是现在的问题是我们不知道每个样本它是属于哪个高斯分量的，也就是说这里边存在一个隐变量，比如说这个隐变量叫zi，zi表示第i个样本它是属于第几个高斯分量的，如属于第一个高斯分量它的值为1、属于第二个高斯分量它的值为2，但是这个值我们是不知道的，最根本的困难就是这个东西所导致的，一旦我们知道每个样本是属于哪个高斯分量的，不光我们可以把高斯分布的μ和Σ算出来，我们还可以把它的权重算出来，因为如果我们已经明确的知道100个训练样本里边有30个是属于N1（第一个高斯分量），那就可以用30/100，得到第一个高斯分量的权重是0.3，但现在的问题是，不幸的是并不知道这100个样本它分别都属于哪一个高斯分量。

EM算法：

既然我们用最大似然估计求不出我们的μ、Σ、w的，这时候EM期望最大化算法登场了，这节课只是讲一下它在高斯混合模型中的一个实际的应用，我们给它一个直观的解释但是我们不做理论上的推导和证明，理论上的推导和证明我们会放在后边的聚类算法里边去深讲，所以先建立一个直观的概念对以后理解后边的推导和证明过程会有好处的，它的算法思想怎么做的呢？

尽然要估计权重系数，均值向量，协方差矩阵的话，那我就像梯度下降法一样用迭代法，先猜一个值出来，猜一组权重、一组协方差矩阵、一组均值向量出来，然后作为一个初始估计值，除了猜这个东西以外，我们还要猜每个样本他都属于第几个高斯分量的，我们真正实现的时候，如像刚才那个例子，该高斯混合模型它有三个高斯分量N1、N2、N3，我们有100个训练样本，我们干脆就把前边30个样本分配到N1分量中去、中间30个分配到N2分量里边去、最后40个分配给N3，随机分配之后就可以算出一个均值向量、协方差矩阵出来，接下来依靠μ、Σ来计算每个样本属于每个高斯分量的概率值，其实就相当于把w给算出来了即算了一个分配方案Γ出来，Γij是第i个样本属于第j个分量的概率，算出来之后就知道每个样本属于哪个高斯分量了，反过来就可以计算每个分量的μ、Σ、w，这样的话就破除了这样的一个依赖，困难就是先有鸡还是先有蛋这样一个循环依赖的存在，并不知道每一个样本它是属于第几个高斯分量的，也就是说它属于每个高斯分量的概率我们是不知道的，但是我们算每个高斯分量它的均值μ、协方差矩阵、权重，我们又依赖这个分配方案即依赖于要知道每个样本它属于第几个高斯分量的，这样就形成了一个相互依赖，我们计算高斯分量的参数需要依赖这个分配方案，但是样本属于第几个高斯分量又依赖于我们的均值μ、Σ、w，因为我们只有根据权重、均值μ、协方差矩阵Σ才能把样本属于每个高斯分量的概率算出来，才能知道样本是属于哪个分量的，因此这里我们就破除这样的一个循环圈的依赖，给他们一个出事的猜测值，然后再转起来，最后收敛到一个最优解上面去，这就是EM算法的核心思想，就是给样本一个初始化的分配方案出来，其实就是给各个高斯分量分配一下样本，根据这些样本来计算它的均值、协方差矩阵、它的权重系数，完成之后，我们根据当前的猜测值u、Σ、w可以计算样本属于每个高斯分量的概率值，然后又可以根据这样一个概率值更新均值、协方差矩阵、权重系数。

具体算法流程：

整个EM算法分两步：

E步：我们给每个分量一个μi、Σi、wi一个不太靠谱的猜测值，把一堆样本随机的分配到每个高斯分量中去，根据这样的一个初始值来计算每个样本属于每个分量的概率值Γij。

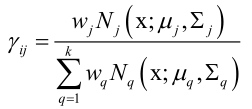
分子是权重乘以每个高斯分量发生的概率值。然后根据该概率Γij估计高斯模型的参数。.

M步，计算模型的参数：

如果是正常的高斯分布，它的均值等于所有样本之和除以样本总数，但是有了样本的权重之后，均值、协方差同理：

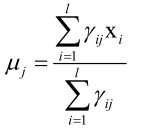
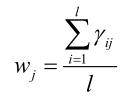
怎么判断算法最后收敛没有？由参数组成的向量两次迭代变化非常小时算法收敛：

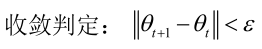
算法的收敛性是有保证的，后边讲聚类算法的时候会做一个严格的证明的。

EM算法实现细节与面临的问题：

参数初始化问题，wi、μi、Σi是随机初始化的，其实初始化的值是不靠谱的，但是神奇的是即使初始化的值不太靠谱算法同样的会收敛到一个解上边去。高斯分量的个数k是人工指定的，各个类的均值和协方差可以按对训练样本随机分配的方案进行计算，同样的，权重也按照随机分配的方案进行计算。

算法的收敛性问题，只能保证收敛到局部最优解，这个局部最优解是和初始值的选定有关的，初始值是随机化的初始值，所以说随机到不同的地方的话最后它收敛到的局部最优解是不一样的，所以一定要小心，EM算法从理论上没法保证收敛到一个全局最优解上边去的。

应用-视频背景建模：

前面讲完了理论，这里讲一下高斯混合模型在视频背景建模方面的应用。背景建模就是，如视频监控中，对运动的东西如人、车进行监控，对于不动的东西如墙、桌子等我们是不监控的。

背景建模的目标：根据历史帧学习得到一个背景模型，从而分割出前景运动目标，被广泛应用于智能视频监控，是整个智能视频监控里边最核心最基础的一个算法。

本质上是机器学习里边的一个二分类问题，判断每个像素是前景还是背景，前提条件是摄像机固定不动。

P. KaewTraKulPong and R. Bowden. An improved adaptive background mixture model for real-time tracking with shadow detection. in European Workshop on Advanced Video Based Surveillance Systems,(London, UK), September 2001.

为什么要用多个正态分布来表示每个像素颜色值的概率分布，因为单纯用一个高斯分布的话是不合适的，其实和前边介绍的白人、黑人、黄人肤色分布是一样的道理，比如说画面中同样的一个位置，当有阴影的时候、白天的时候、晚上的时候、日出日落的时候，它的状态的不一样的，包括被树叶刮风震荡档住，所以只用一个高斯分布来表示是不行的，得用多个来表示，可能有多种不同的状态，在每种状态下它都服从一种高斯分布，那看这个模型是怎么建立起来的：

在每个时刻t，一个像素的颜色的概率用高斯混合模型表示：

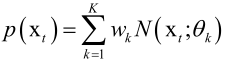
这里每个高斯分布都是一个三维的正态分布：

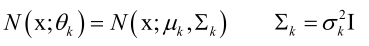，RGB各有一个均值然后它们组成均值向量μk，为了问题的简化这里协方差矩阵做了一个偷懒，表示RGB三个分量之间是没有任何关系的，但是实际上它是有关系的，RGB三个颜色值之间肯定是有关系的他们之间是相关的，因此这里这种假设是有损失的，而且这三个分量的协方差是一样的，按照这样来做的，这样可以简化问题的求解。

假设任意一个像素值可以用k个高斯分量来表示，这些高斯分量按照w_k/σ_k的值(实际上这个就代表该高斯分量它的一个置信度，它的权重越大、变化范围越小，它的置信度会越大)从大到小排序，然后这k个高斯分量的前面的B个分量被用来作为背景分量。根据置信度对高斯分量排序，第一个置信度最高，依次递减，比如人工指定参数k为5，可能选前四个高斯分量作为背景模型，另外一个作为前景的模型，前边4个代表着这个像素处于背景状态的时候它的各种不同的概率分布。B是怎么确定的呢？前边最大的B个它累加起来的概率值要大于给定的阈值T，因为所有的wi加起来等于1，T如果取0.9，则以0.9的概率是背景，所有时刻的统计有0.9的概率该像素是处于背景状态的。

那怎么具体做背景建模呢，怎么把前景给分割出来的。来了一个当前帧（一张图像），我们就一次处理他的每个像素值，从左到右从上到下，把每个位置的像素拿来判断一下，拿一个位置的像素和它的每个高斯分量比较一下，如果和前面B个高斯分量中的任何一个匹配((x-μ)/σ<2.5σ成立则匹配成功，认定为该像素是一个背景像素)，则被认为是背景像素；否则是前景像素。

然后根据上边的分类结果，更新我们的高斯分布，分两种情况，如果一个像素被判定为背景像素，则更新与它匹配的那个高斯分量的参数。

如果一个像素被判定为前景像素，则将最后一个高斯分量替换掉，用当前像素进行初始化。

网上是有很多开源的代码实现高斯混合模型的背景建模的，像MoG的背景建模，opencv中有对应的实现。

本集总结：

首先介绍了GMM的基本思想和原理。

接下来用了一个肤色的实际例子做了说明加深对算法的理解。

然后介绍这种算法在训练的时候估计它的参数θ面临的问题。

接下来介绍了EM算法。

介绍完算法原理以后，用了一个实际的例子MoG的背景建模（高斯混合模型的背景建模）来讲了它的一个实际的应用。