NLP中一些数学知识

1.所谓概率函数就是要在整个样本空间分配概率值，概率值总和为1

2.一个完备的概率空间应该由样本空间，概率函数和事件域这三部分组成，在统计自然语言处理中，我们的目标就是为建立的模型定义一个符合上述条件的概率空间。

3.随机变量有一个取值的范围，因此我们避免了直接和事件本身打交道，而是处理代表它们的随机变量的值，为了更清楚的描述随机变量的特性，我们引入概率密度函数的概念，它表示随机变量取不同值的概率。

4.期望值是一个随机变量的各个取值的平均值。一个随机变量的方差描述该随机变量的值偏离其期望值的程度。在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。 假设一个质地均匀的骰子，即每一面出现的概率都为1/6，则它的期望值为21/6，这个期望值表示多次掷骰子实验得到的总点数和除以实验的次数。（相当于均值）

5.我们用联合概率分布来描述样本空间中多个随机变量的分布，设两个离散型随机变量X和Y，他们的联合密度函数可写为

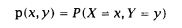
条件概率密度公式

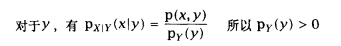
6.离散分布函数：二项分布 当重复一个只有两种输出（假设0和1）的实验，并且各次实验之间相互独立时，我们就说实验的结果服从二项分布。二项分布在统计自然语言处理中应用的很广泛，例如估计英文文本中含有单词the的句子所占的百分比。

7.连续分布函数：二项分布

当重复一个只有两种输出（假设0和1）的实验，并且各次实验之间相互独立时，我们就说实验的结果服从二项分布。二项分布在统计自然语言处理中应用的很广泛，例如估计英文文本中含有单词the的句子所占的百分比。

8.极大似然估计 仍以抛硬币为例，假设我们重复10次，其中8次结果是正面朝上的，从一个频度论者的角度来看，他会认为10次实验中8次正面朝上是一种极大似然估计。

9.熵表示单个随机变量的不确定性的均值，随机变量的熵越大，它的不确定性越大，也就是说能正确估计其值的概率越小。熵值度量了随机变量所包含的信息量的大小。熵可以用于衡量事件不确定的大小，事件所透漏出来的信息越多，其熵值会越小。

10.词干提取不注意词法会丢失一些信息

11.应该用什么特征来指导设计标注集呢？通常，一个标注集同时依据分类目标特征和预测特征来进行编码，分类目标特征告诉用户关于一个词的语法类别的有用信息，预测特征是对预测上下文中其它词语特性有用的特征，他们通常是相互交叉的，但是没有必要等同看待。

12.联合分布函数（联合概率分布）

联合分布函数(joint distribution function)亦称多维分布函数。以二维情形为例，设（X，Y）是二维随机变量，x，y是任意实数，二元函数：F(x,y)=P({X≤x∩Y≤y})=P(X≤x,Y≤y)，被称二维随机变量(X，Y)的分布函数，或称为X和Y的联合分布函数。

在许多生产实际与理论研究中，一个随机现象常常需要同时用几个随机变量去描述，所以要使用联合密度函数。

13、联合概率分布和概率分布

多维随机变量的分布才被称为联合概率分布，普通的一维随机变量其分布一般称为概率分布。所以，只是多维和一维情形下不同的叫法而已。

14.边缘分布函数

如果二维随机变量X,Y的分布函数F{x,y}为已知，那么随机变量x，y的分布函数F�{x}和Fʏ{y}可由F{x,y}求得。则F�{x}和Fʏ{y}为分布函数F{x,y}的边缘分布函数

15.欧式距离、余弦相似度、余弦距离

公式见：https://zhuanlan.zhihu.com/p/84643138

区别见：https://www.cnblogs.com/chaosimple/p/3160839.html

余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。

借助三维坐标系来看下欧氏距离和余弦距离的区别：

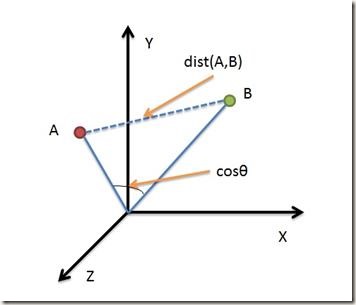
从上图可以看出，欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。如果保持A点位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦距离 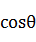 是保持不变的（因为夹角没有发生变化），而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦距离之间的不同之处。

欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：

欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。

余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

欧式距离越小越相似，余弦相似度越大越相似，余弦相似度取值范围为[-1,1]

余弦距离=1-余弦相似度，取值为[0,2]