P5025 [SNOI2017]炸弹

原题链接  https://www.luogu.org/problem/P5025

闲话时刻：

第一道 AC 的黑题，虽然众人皆说水。。。

其实思路不是很难，代码也不是很难打，是一些我们已经学过的东西凝合在一起，只要基础扎实的话，做出这道题目来说也就很简单了（不包括我）；

题目大意：

有 n 个点，每个点可影响到它左右各 R [ i ] 范围内的点，并且影响到的点会产生连锁反应，求每个点能影响到多少个点；

题解：

一个很简单的思路：

向每个炸弹爆炸范围内的其他炸弹连一条有向边 < u , v >，表示 u 能炸到 v，最后我们从每个点开始跑 dfs，看看能到达多少个点就好了；

但是。。。

这样连边的话，最劣情况下会连 n² 条边，看一眼 n 的范围：N ≤ 500000，嗯，显然不行 ~o(*￣▽￣*)o；

考虑建边优化：

不难想到一个炸弹的爆炸范围是一个长度为 2 * R [ i ] 的区间，这个区间内的所有炸弹都会被引爆，因此被引爆的炸弹也是一个连续的区间；

区间操作？你想到了什么？

线段树优化建边

假如说一个炸弹 x 能炸到第 2~6 个炸弹，考虑怎么建边：

一般操作：

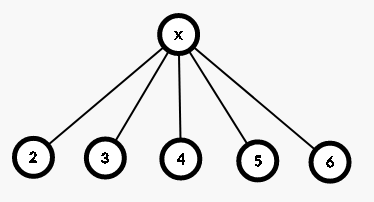
线段树优化建边：

建了 5 条边？看我的！

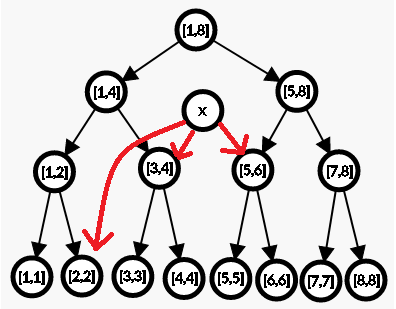
我们发现，这种建边方式只需要建 ⌈ log₂ 5 ⌉ = 3 条边；

看了上面的图，应该对线段树优化建边有了一个初步的认识了：

我们将线段树上原有的边也看作是我们建边的一部分，每次单点向区间建边时，向线段树区间查询那样，一直递归下去形成若干个小区间，向这些小区间建边；查询的话可以通过线段树原有的边来访问到叶子节点；

再具体一点，假如第 2 个炸弹能炸到第 4~8 个炸弹，那么建边就是这样的：

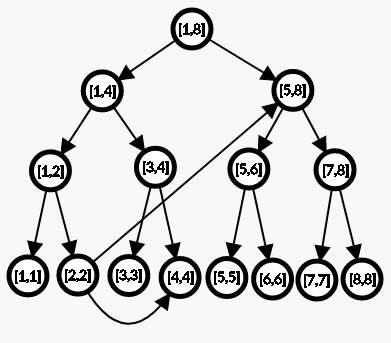
这样虽然 2 连向了 [ 5 , 8 ] 这个节点，但是我们能通过继续往下递归找到 5，6，7，8 点，从而达到优化建边的目的；

建完边了，但是这边还是有点多哦，看起来很乱，缩点试试？

缩点是可以的，假如一个环内的任意一个炸弹被引爆了，那么整个环内的所有炸弹都会被引爆，所以我们不妨将这一环内的炸弹看作是一个大炸弹；

然后我们就又用到了 tarjan 缩点；

这个就不多说了，大家应该都会；

然后对于每个强联通分量，我们都 dfs 一遍累加它能到达的所有强联通分量的大小，这个题就做完了；

woc？这么简单？

没错就是这么简单qwq！

细节提示

这道题思路挺简单的，但是里面的坑真不少，归结一下我掉进的坑，顺便提醒您们一下哦：

1. 每个强联通分量的大小不是里面的节点个数，而是里面的叶子节点个数（炸弹数），那些区间节点是不能被包含在内的；

2. dfs 的过程中，强联通分量之间可能会有重边，记得记录一下，防止重复计算；

在这里解释一下为什么有重边：

比如说这个缩点之前的奇奇怪怪的图：

嗯，是没有重边，缩完点之后呢？

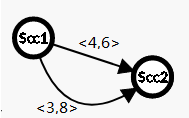
对吧。

3. 注意开 long long！

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const int N=;
const long long mod=;
long long n,tim,top,maxn,scc_sum,edge_sum,Edge_sum;
long long zb[N],R[N],num[N],where[N],head[N],Head[N],dfn[N],low[N],vis[N],st[N],scc[N];
long long ans[N],sum,size[N];
vector<int> son[N<<];
struct node
{
    int to,from,next;
}a[N<<],b[N<<];
void add(int from,int to)    //链表建图,应用于线段树上
{
    edge_sum++;
    a[edge_sum].next=head[from];
    a[edge_sum].to=to;
    a[edge_sum].from=from;
    head[from]=edge_sum;
}
void build(long long node,int l,int r)
{
    if(l==r)
    {
        where[l]=node;       //坐标为l的炸弹在线段树的第node个节点
        maxn=max(maxn,node); //记录线段树上最大的节点编号是多少
        num[node]=;         //表示线段树上的第node个节点是叶子节点
        return ;
    }
    int mid=(l+r)>>;
    add(node,node<<);
    add(node,node<<|);      //向左右子树建边
    build(node<<,l,mid);     //递归
    build(node<<|,mid+,r);
}
void Add(int node,int l,int r,int x,int y,int v)
{
    if(x<=l&&r<=y)
    {
        add(v,node);          //点向区间连边
        return ;
    }
    int mid=(l+r)>>;
    if(x<=mid) Add(node<<,l,mid,x,y,v);
    if(y>mid)  Add(node<<|,mid+,r,x,y,v);
}
void tarjan(int u)            //tarjan缩点
{
    dfn[u]=low[u]=++tim;
    st[++top]=u;
    vis[u]=;
    for(int i=head[u];i;i=a[i].next)
    {
        int v=a[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        scc_sum++;
        while(st[top]!=u)
        {
            vis[st[top]]=;
            scc[st[top]]=scc_sum;
            size[scc_sum]+=num[st[top]];  //坑点1:注意只记录叶子节点(炸弹)个数,而不是节点个数,num只有叶子节点才有值
            top--;
        }
        //把u弹出去(表示不会do while)
        vis[st[top]]=;
        scc[st[top]]=scc_sum;
        size[scc_sum]+=num[st[top]];
        top--;
    }
}
void rebuild()
{
    for(int i=;i<=edge_sum;i++)         //线段树上所有的边
    {
        int u=a[i].from;
        int v=a[i].to;
        if(scc[u]!=scc[v])
        son[scc[u]].push_back(scc[v]);     //vector存图,比较方便
    }
}
void dfs(int u)
{
    if(ans[u]) return ;                  //记搜
    ans[u]=size[u];                      //首先一个强联通分量里的点都能互相到达
    for(int i=;i<son[u].size();i++)
    {
        int v=son[u][i];
        dfs(v);
    //这里有个vis数组判重边用的特别精髓,给大家解释下:
    //vis[i]:表示本轮从哪个点到的i
    //想一想:假如u->v有两条边,那么在走第一条边的时候,vis[v]就会被标记u,那么在遍历第二遍的时候就直接continue了,不会重复计算
    //vis数组可以不用清空
        if(vis[v]==u) continue;
        vis[v]=u;
        ans[u]=(ans[u]+ans[v])%mod;
    }
}
int main()
{
    n=read();                    //n个炸弹
    for(int i=;i<=n;i++)
    {
        zb[i]=read();            //炸弹的位置,题目保证是严格递增的了
        R[i]=read();             //炸弹的爆炸半径
    }
    build(,,n);                //线段树建树
    for(int i=;i<=n;i++)        //将每个炸弹与能炸到的炸弹区间连边
    {
        long long l=lower_bound(zb+,zb++n,zb[i]-R[i])-zb;  //找到能炸到的最左边的炸弹
        long long r=upper_bound(zb+,zb++n,zb[i]+R[i])-zb-;//找到能炸到的最右边的炸弹
        Add(,,n,l,r,where[i]); //连边,where[i]表示炸弹i在线段树上是哪个节点,不懂的结合上面的图体会一下
    }
    for(int i=;i<=maxn;i++)     //缩点操作,注意这里是对线段树上的所有点进行缩点,不单单是叶子节点
    {
        if(!dfn[i]) tarjan(i);   //图不一定联通,多进行几次
    }
    rebuild();                   //对缩完点后的DAG进行重新建图
    for(int i=;i<=scc_sum;i++) dfs(i);  //dfs求每个强联通分量能够到达多少个炸弹
    for(int i=;i<=n;i++)        //求答案
    {
        sum=(sum+i*ans[scc[where[i]]]%mod)%mod;
        //where[i]:炸弹i在线段树上是第几个节点
        //scc[i]:编号为i的点在哪个强联通分量里
        //ans[i]:编号为i的强联通分量能够到达多少个炸弹
        //合起来就是:炸弹i在线段树上所对应的节点所在的强联通分量能到达多少个炸弹,are you ok?
    }
    printf("%lld\n",sum%mod);
    return ;
}

然后发现跑的有点慢能A不就行了嘛：

主要是在 dfs 的时候 vector 就显得很慢了，所以我们重建图的时候可以先用链表建图，等跑完 dfs 之后再用 vector 存儿子判重边就好了：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const int N=;
const long long mod=;
long long n,tim,top,maxn,scc_sum,edge_sum,Edge_sum;
long long zb[N],R[N],num[N],where[N],head[N],Head[N],dfn[N],low[N],vis[N],st[N],scc[N];
long long ans[N],sum,size[N];
struct node
{
    int to,from,next;
}a[N<<],b[N<<];
void add(int from,int to)    //链表建图,应用于线段树上
{
    edge_sum++;
    a[edge_sum].next=head[from];
    a[edge_sum].to=to;
    a[edge_sum].from=from;
    head[from]=edge_sum;
}
void readd(int from,int to)
{
    Edge_sum++;
    b[Edge_sum].from=from;
    b[Edge_sum].to=to;
    b[Edge_sum].next=Head[from];
    Head[from]=Edge_sum;
}
void build(long long node,int l,int r)
{
    if(l==r)
    {
        where[l]=node;       //坐标为l的炸弹在线段树的第node个节点
        maxn=max(maxn,node); //记录线段树上最大的节点编号是多少
        num[node]=;         //表示线段树上的第node个节点是叶子节点
        return ;
    }
    int mid=(l+r)>>;
    add(node,node<<);
    add(node,node<<|);      //向左右子树建边
    build(node<<,l,mid);     //递归
    build(node<<|,mid+,r);
}
void Add(int node,int l,int r,int x,int y,int v)
{
    if(x<=l&&r<=y)
    {
        add(v,node);          //点向区间连边
        return ;
    }
    int mid=(l+r)>>;
    if(x<=mid) Add(node<<,l,mid,x,y,v);
    if(y>mid)  Add(node<<|,mid+,r,x,y,v);
}
void tarjan(int u)            //tarjan缩点
{
    dfn[u]=low[u]=++tim;
    st[++top]=u;
    vis[u]=;
    for(int i=head[u];i;i=a[i].next)
    {
        int v=a[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        scc_sum++;
        while(st[top]!=u)
        {
            vis[st[top]]=;
            scc[st[top]]=scc_sum;
            size[scc_sum]+=num[st[top]];  //坑点1:注意只记录叶子节点(炸弹)个数,而不是节点个数,num只有叶子节点才有值
            top--;
        }
        //把u弹出去(表示不会do while)
        vis[st[top]]=;
        scc[st[top]]=scc_sum;
        size[scc_sum]+=num[st[top]];
        top--;
    }
}
void rebuild()
{
    for(int i=;i<=edge_sum;i++)         //线段树上所有的边
    {
        int u=a[i].from;
        int v=a[i].to;
        if(scc[u]!=scc[v])
        //son[scc[u]].push_back(scc[v]);     //vector存图,比较方便
        readd(scc[u],scc[v]);
    }
}
void dfs(int u)
{
    /*if(ans[u]) return ;                  //记搜
    ans[u]=size[u];                      //首先一个强联通分量里的点都能互相到达
    for(int i=0;i<son[u].size();i++)
    {
        int v=son[u][i];
        dfs(v);
    //这里有个vis数组判重边用的特别精髓,给大家解释下:
    //vis[i]:表示本轮从哪个点到的i
    //想一想:假如u->v有两条边,那么在走第一条边的时候,vis[v]就会被标记u,那么在遍历第二遍的时候就直接continue了,不会重复计算
    //vis数组可以不用清空
        if(vis[v]==u) continue;
        vis[v]=u;
        ans[u]=(ans[u]+ans[v])%mod;
    }*/
    if(ans[u]) return ;
    ans[u]=size[u];
    vector<int> son;
    for(int i=Head[u];i;i=b[i].next)
    {
        int v=b[i].to;
        dfs(v);son.push_back(v);      //把点u的所有儿子放进vector里
    }
    for(int i=;i<son.size();i++)
    {
        if(vis[son[i]]==u) continue;
        vis[son[i]]=u;
        ans[u]=(ans[u]+ans[son[i]])%mod;
    }
}
int main()
{
    n=read();                    //n个炸弹
    for(int i=;i<=n;i++)
    {
        zb[i]=read();            //炸弹的位置,题目保证是严格递增的了
        R[i]=read();             //炸弹的爆炸半径
    }
    build(,,n);                //线段树建树
    for(int i=;i<=n;i++)        //将每个炸弹与能炸到的炸弹区间连边
    {
        long long l=lower_bound(zb+,zb++n,zb[i]-R[i])-zb;  //找到能炸到的最左边的炸弹
        long long r=upper_bound(zb+,zb++n,zb[i]+R[i])-zb-;//找到能炸到的最右边的炸弹
        Add(,,n,l,r,where[i]); //连边,where[i]表示炸弹i在线段树上是哪个节点,不懂的结合上面的图体会一下
    }
    for(int i=;i<=maxn;i++)     //缩点操作,注意这里是对线段树上的所有点进行缩点,不单单是叶子节点
    {
        if(!dfn[i]) tarjan(i);   //图不一定联通,多进行几次
    }
    rebuild();                   //对缩完点后的DAG进行重新建图
    for(int i=;i<=scc_sum;i++) dfs(i);  //dfs求每个强联通分量能够到达多少个炸弹
    for(int i=;i<=n;i++)        //求答案
    {
        sum=(sum+i*ans[scc[where[i]]]%mod)%mod;
        //where[i]:炸弹i在线段树上是第几个节点
        //scc[i]:编号为i的点在哪个强联通分量里
        //ans[i]:编号为i的强联通分量能够到达多少个炸弹
        //合起来就是:炸弹i在线段树上所对应的节点所在的强联通分量能到达多少个炸弹,are you ok?
    }
    printf("%lld\n",sum%mod);
    return ;
}

嗯，果然在时间和空间上都有很大的优化哦~