算法(贪心|BF|KMP)

贪心算法

前置知识

const Greedy = num => {
//贪心
  let arr = [100, 20, 10, 5, 2, 1]
  let count = 0;
  for (let i = 0; i < arr.length; i++) {
    let use = Math.floor(num / arr[i])
    count += use;
    num = num - arr[i] * use
    console.log('需要面额为' + arr[i] + '有' + count + '张')
    count = 0;
  }
}
Greedy(120)

一群孩子吃糖果

// 孩子,糖果,
const findContent = (g, s) => {
  g.sort()
  s.sort()
  let child = 0;
  let cookie = 0;
  while (child < g.length && cookie < s.length) {
    if (g[child] <= s[cookie]) {
      child++
    }
    cookie++;//无论成功或者失败,每个糖果只尝试一次,cookie向后移动
  }
  return child
}
let g = [2, 4, 5, 6, 7]
let s = [1, 3, 4, 6, 7]
console.log(findContent(g, s))

摇摆序列(LeetCode376)

举例子

[1,17,5,10,13,15,10,5,16,8]

​ [5,10,13,15] 属于递增序列

也就是[小大小大...]或者[大小大小...]

求最长的摇摆序列

const wiggleMax = nums => {
  let n = nums.length
  if (n < 2) {
    return n
  }
  let up = 1;
  let down = 1;
  for (let i = 1; i <n ; i++) {
    if (nums[i] > nums[i - 1]) {
      up=down+1;
    }
    if (nums[i] < nums[i - 1]) {
      down=up+1;
    }
  }
  return Math.max(up, down)
}
console.log(wiggleMax([1, 17, 5, 10, 13, 15, 10, 5, 16, 8,1,9]))

402移掉k位数字

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小

初始化一个栈

记得打断点就懂了

class Stack {
  constructor() {
    this.items = []
  }

  push(element) {
    this.items.push(element)
  }

  //移除栈中的元素,遵循先进后出原则
  pop() {
    return this.items.pop()
  }

  //返回栈顶
  peek() {
    return this.items[this.items.length - 1]
  }

  //判断栈是否为空,为空为true,不为空为false
  isEmpty() {
    return this.items.length == 0
  }

  size() {
    return this.items.length
  }

  //清除栈
  clear() {
    this.items = [];
  }

  print() {
    console.log(this.items)
  }
}

const removeK = (num, k) => {
  //存在的栈
  const stack = new Stack();
  //贪心算法+栈
  if (k >= num.length || num.length == 0) return '0';
  //栈顶始终是最大值
  stack.push(+num.charAt(0));
  for (let i = 1; i < num.length; i++) {
    let now = +num.charAt(i);
    //当前栈不为空的时候,而且k>0,当前值小于栈顶,就删除栈中的一个元素
    while (!stack.isEmpty() && k > 0 && now < stack.peek()) {
      stack.pop();
      k--;
    }
    //不等于0可以添加进去,
    //等于0，栈不为空可以填进去，
    if (now != 0 || !stack.isEmpty()) {
      stack.push(now);
    }
  }
  //56789去掉后面添加的个人
  while (k > 0) {
    k--;
    stack.pop();
  }
  //10，1(当now=0时，满足条件，去掉1，但now为0，且为空。)
  if (stack.isEmpty()) {
    return '0';
  }
  //把栈中元素放到数组中
  let sb = [];
  while (!stack.isEmpty()) {
    sb.push(stack.pop());
  }
  //还原成字符串
  let sub = '';
  sb.reverse().map(val => sub += val)
  return sub
}
console.log(removeK('9234567', 3))

跳跃游戏

给出一个非负整数数组，你最初定位在数组的第一个位置。

数组中的每个元素代表你在那个位置可以跳跃的最大长度。

判断你是否能到达数组的最后一个位置。

样例

A = [2,3,1,1,4]，返回 true.

A = [3,2,1,0,4]，返回 false.

const canJump = maxSteps => {
  if (maxSteps == null || maxSteps.length == 0) {
    return false;
  }
  let meetIndex = maxSteps.length - 1;
  for (let i = maxSteps.length - 1; i >= 0; i--) {
    if (i + maxSteps[i] >= meetIndex) {
      meetIndex = i;
    }
  }
  return meetIndex == 0;
}
console.log(canJump([0,2,0,1,4]))

C++基础

>> 赋值

<< 打印

-> .

直方图中最大矩形面积

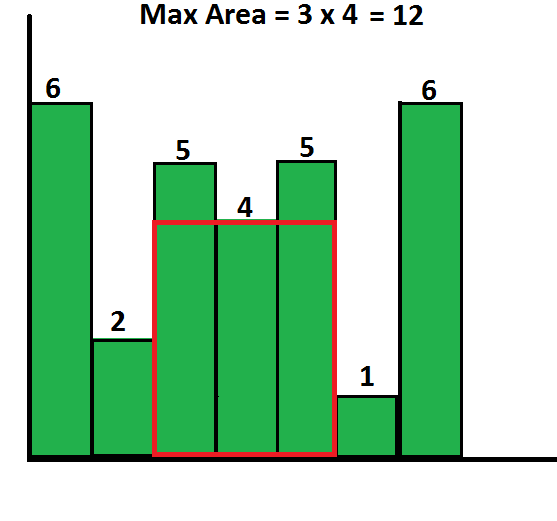
const getAnswer = h => {
  let n = h.length;
  let ans = 0;
  for (let i = 1; i < n; i++) {
    let a = Infinity;
    for (let j = i; j < n; j++) {
      a = Math.min(a, h[j])
      ans = Math.max(ans, (j - i + 1) * a)
    }
  }
  return ans
}
console.log(getAnswer([1, 8, 3, 4, 8]))

请n项的和

递归版

const sum2=num=>{
  if (num < 1) {
    return 0
  }
  return sum2(num-1)+num
}
console.log(sum2(100))

非递归版

const sum1=n=>{
  let result=0;
  for (let i = 0; i <=n; i++) {
    result+=i;
  }
  return result
}
console.log(sum1(100))

线性表

顺序存储是顺序表

链表是线性表的链式存储方式,不连续的

-数据的元素|下一个元素的地址

字符串

字符串的存储可以使用顺序存储和链式存储两种方式

BF算法: BF是蛮力,暴力穷举

BF算法 O(m*n)

const BF = (s, t, pos) => {
  let i = pos,
    j = 1,
    sum = 0;
  let slen = s.length
  let tlen = s.length
  while (i <= slen && j <= tlen) {
    sum++
    //如果相等,则继续比较后面的字符
    if (s[i - 1] == t[j - 1]) {
      i++
      j++
    } else {
      //i回退到上一轮开始比较的下一个字符
      i = i - j + 2
      //j回退到第1个字符
      j = 1;
    }
  }
  return '一共比较了' + sum + '次'

}
console.log(BF('abcbcd', 'bcd', 0))

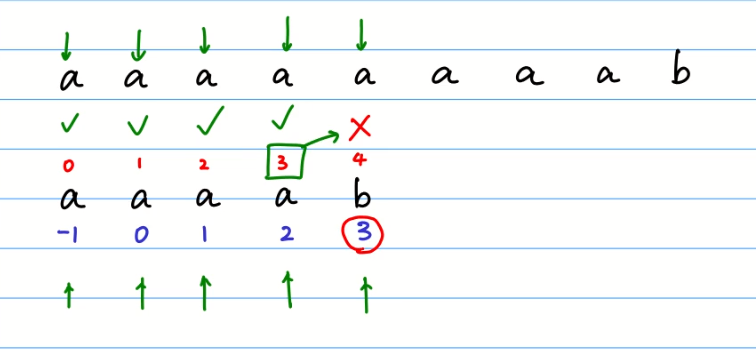
KMP算法 O(n+m)

使用动态规划解决

真前缀 除了自身以外,一个字符串的全部头部组合

后前缀 除了自身之外,一个字符串的全部尾部组合

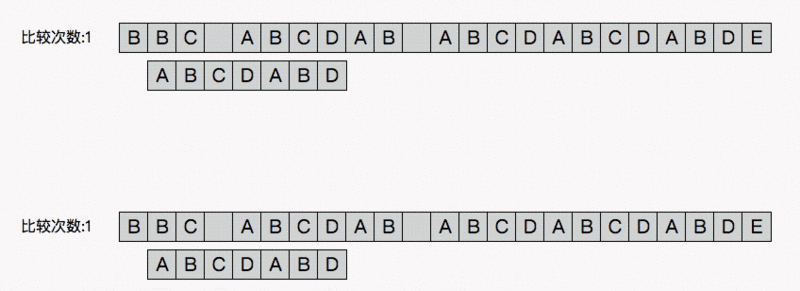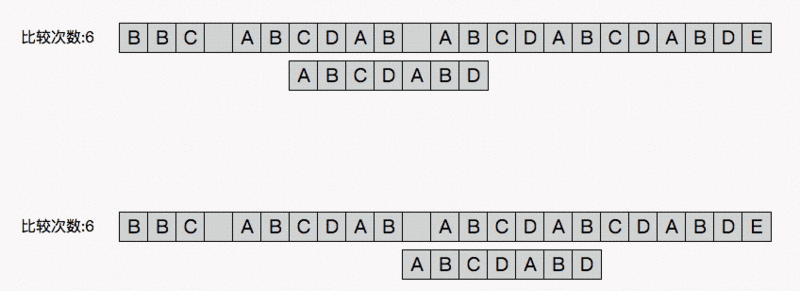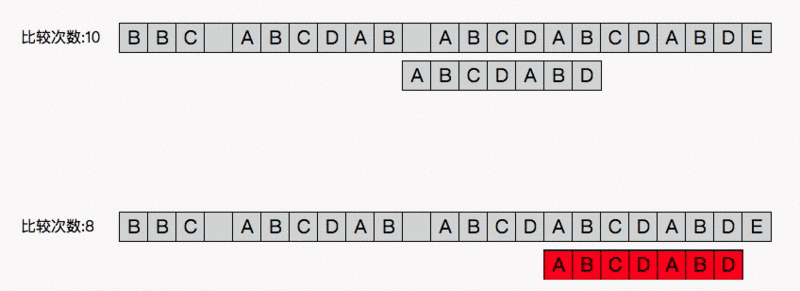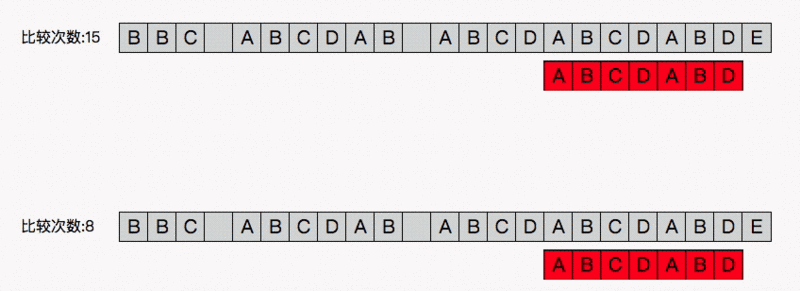
动画

算出最长公共前后缀的长度(重复的长度)

开始比较(把数组下标为3的向前走一位)

写的很乱,现在重新分析下

移动的位数=匹配的字符数-对应的部分匹配值 //4-3=1 ,移动一位

我们算算匹配表的分解,p表示前缀,n表示后缀,r表示结果

a,         p=>0, n=>0  r = 0

aa,        p=>[a]，n=>[a] , r = a.length => 1

aar,       p=>[a,aa], n=>[r,ar]  ,r = 0

aaro,      p=>[a,aa,aar], n=>[o,ra,aro] ,r = 0

aaron      p=>[a,aa,aar,aaro], n=>[n,on,ron,aron] ,r = 0

aarona,    p=>[a,aa,aar,aaro,aaron], n=>[a,na,ona,rona,arona] ,r = a.lenght = 1

aaronaa,   p=>[a,aa,aar,aaro,aaron,aarona], n=>[a,aa,naa,onaa,ronaa,aronaa] ,  r = Math.max(a.length,aa.length) = 2

aaronaac   p=>[a,aa,aar,aaro,aaron,aarona], n=>[c,ac,aac,naac,onaac,ronaac]  r = 0

终于找到了看着比较舒服的完整代码了,不多说直接上代码

const getNext = str => {
    let next = [-1]
    let k = -1
    for (let i = 1; i < str.length; i++) {
           //第一次不执行且从前缀开始,判断不同的把-1赋值上
        while (k != -1 && str[k + 1] != str[i]) {
            k = next[k]
        }
         //然后判断相同的,让k自增
        if (str[k + 1] == str[i]) {
            k++
        }
        //这是最开始将k赋值到数组中,然后依次判断把值赋值上
        next[i] = k
    }
    return next
}

const KMP = (str1, str2) => {
    let next = getNext(str2)
    let j = 0

    for (let i = 0; i < str1.length; i++) {
        while (j > 0 && str1[i] != str2[j]) {
            j = next[j - 1] + 1 // j 更新为最长可匹配前缀子串的长度 k
        }
        if (str1[i] == str2[j]) j++
        if (j == str2.length) return i - str2.length + 1
    }
    return -1
}
console.log(KMP('abcdacbcdababc', 'ababc'))

##########################..........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................