Stacked Autoencoders

转自：http://www.cnblogs.com/tornadomeet/archive/2013/03/25/2980357.html

如果使用多层神经网络的话，那么将可以得到对输入更复杂的函数表示，因为神经网络的每一层都是上一层的非线性变换。当然，此时要求每一层的activation函数是非线性的，否则就没有必要用多层了。

Deep networks的优点：

一、比单层神经网络能学习到更复杂的表达。比如说用k层神经网络能学习到的函数（且每层网络节点个数时多项式的）如果要用k-1层神经网络来学习，则这k-1层神经网络节点的个数必须是指数级庞大的数字。

二、不同层的网络学习到的特征是由最底层到最高层慢慢上升的。比如在图像的学习中，第一个隐含层层网络可能学习的是边缘特征，第二隐含层就学习到的是轮廓什么的，后面的就会更高级有可能是图像目标中的一个部位，也就是是底层隐含层学习底层特征，高层隐含层学习高层特征。

三、这种多层神经网络的结构和人体大脑皮层的多层感知结构非常类似，所以说有一定的生物理论基础。

Deep networks的缺点：

一、网络的层次越深，所需的训练样本数越多，如果是用有监督学习的话，那么这些样本就更难获取，因为要进行各种标注。但是如果样本数太少的话，就很容易产生过拟合现象。

二、因为多层神经网络的参数优化问题是一个高阶非凸优化问题，这个问题通常收敛到一个比较差的局部解，普通的优化算法一般都效果不好。也就是说，参数的优化问题是个难点。

三、梯度扩散问题。因为当网络层次比较深时，在计算损失函数的偏导时一般需要使用BP算法，但是这些梯度值随着深度慢慢靠前而显著下降，这样导致前面的网络对最终的损失函数的贡献很小。这样的话前面的权值更新速度就非常非常慢了。一个理论上比较好的解决方法是将后面网络的结构的神经元的个数提高非常多，以至于它不会影响前面网络的结构的学习。但这样岂不是和低深度的网络结构一样了吗？所以不妥。

所以一般都是采用的层次贪婪训练方法来训练网络的参数，即先训练网络的第一个隐含层，然后接着训练第二个，第三个…最后用这些训练好的网络参数值作为整体网络参数的初始值。这样的好处是数据更容易获取，因为前面的网络层次基本都用无监督的方法获得，很容易，只有最后一个输出层需要有监督的数据。另外由于无监督学习其实隐形之中已经提供了一些输入数据的先验知识，所以此时的参数初始化值一般都能得到最终比较好的局部最优解

A stacked autoencoder is a neural network consisting of multiple layers of sparse autoencoders in which the outputs of each layer is wired to the inputs of the successive layer.

Formally, consider a stacked autoencoder with n layers. Using notation from the autoencoder section, let W^(k,1),W^(k,2),b^(k,1),b^(k,2) denote the parameters W⁽¹⁾,W⁽²⁾,b⁽¹⁾,b⁽²⁾ for kth autoencoder. Then the encoding step for the stacked autoencoder is given by running the encoding step of each layer in forward order:

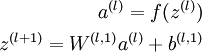
The decoding step is given by running the decoding stack of each autoencoder in reverse order:

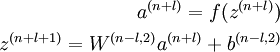
The information of interest is contained within a⁽ⁿ⁾, which is the activation of the deepest layer of hidden units. This vector gives us a representation of the input in terms of higher-order features. —— 高层次特征

Training

A good way to obtain good parameters for a stacked autoencoder is to use greedy layer-wise training. To do this, first train the first layer on raw input to obtain parameters W^(1,1),W^(1,2),b^(1,1),b^(1,2). Use the first layer to transform the raw input into a vector consisting of activation of the hidden units, A. Train the second layer on this vector to obtain parametersW^(2,1),W^(2,2),b^(2,1),b^(2,2). Repeat for subsequent layers, using the output of each layer as input for the subsequent layer.

This method trains the parameters of each layer individually while freezing parameters for the remainder of the model. To produce better results, after this phase of training is complete,fine-tuning using backpropagation can be used to improve the results by tuning the parameters of all layers are changed at the same time.

Example

To give a concrete example, suppose you wished to train a stacked autoencoder with 2 hidden layers for classification of MNIST digits

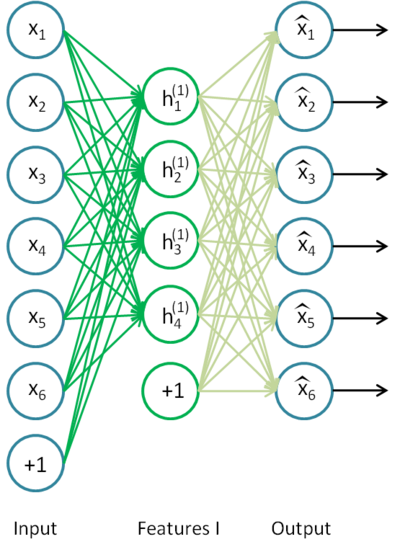
First, you would train a sparse autoencoder on the raw inputs x^(k) to learn primary features h^(1)(k) on the raw input.

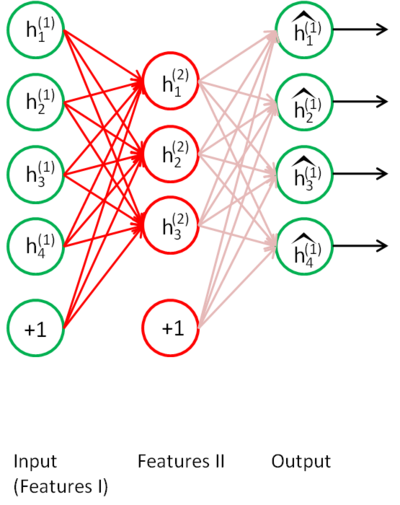
Next, you would feed the raw input into this trained sparse autoencoder, obtaining the primary feature activations h^(1)(k)for each of the inputs x^(k). You would then use these primary features as the "raw input" to another sparse autoencoder to learn secondary features h^(2)(k) on these primary features.

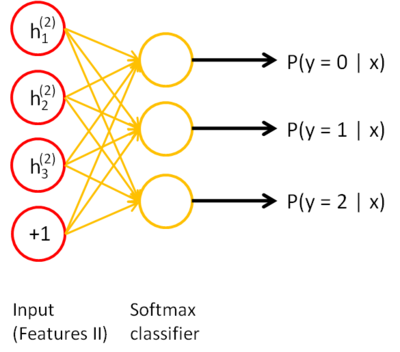
Following this, you would feed the primary features into the second sparse autoencoder to obtain the secondary feature activations h^(2)(k) for each of the primary features h^(1)(k) (which correspond to the primary features of the corresponding inputs x^(k)). You would then treat these secondary features as "raw input" to a softmax classifier, training it to map secondary features to digit labels.

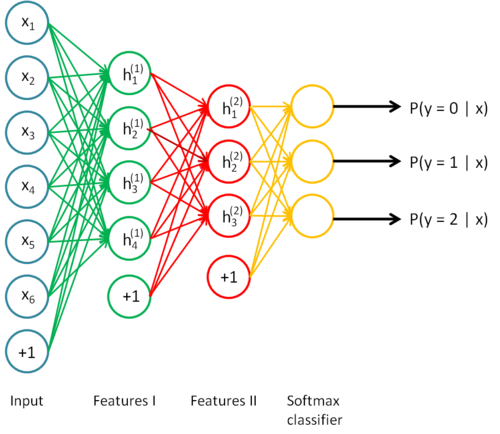
Finally, you would combine all three layers together to form a stacked autoencoder with 2 hidden layers and a final softmax classifier layer capable of classifying the MNIST digits as desired.

由此，层层深入，从发掘简单特征到发掘复杂特征，识别~~