洛谷P3381 【模板】最小费用最大流(dijstra费用流)

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

输入样例#1：复制

输出样例#1：复制

50 280

说明

时空限制：1000ms,128M

（BYX：最后两个点改成了1200ms）

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

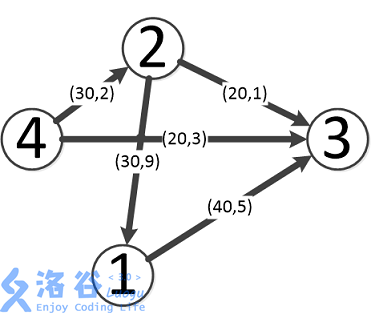
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

dijstra费用流真的不是一般的快

直接吊打SPFA

有一篇写的不错的博客

http://www.yhzq-blog.cc/%E6%9C%80%E5%B0%8F%E8%B4%B9%E7%94%A8%E6%9C%80%E5%A4%A7%E6%B5%81%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93/

另外就是最后一句话为什么是*h，而不是*dis

我个人的理解，因为在求最短路的时候有h的存在，所以这里的dis已经不是实际上的dis，而h才是实际上的dis

// luogu-judger-enable-o2

#include<cstdio>

#include<cstring>

#include<queue>

#define Pair pair<int,int>

#define fi first

#define se second

#define AddEdge(x,y,f,z) add_edge(x,y,f,z);add_edge(y,x,0,-z);

#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++)

char buf[<<],*p1=buf,*p2=buf;

using namespace std;

const int MAXN=1e6+,INF=1e8+;

inline int read()

{

    char c=getchar();int x=,f=;

    while(c<''||c>''){if(c=='-')f=-;c=getchar();}

    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}

    return x*f;

}

int N,M,S,T;

struct node

{

    int u,v,f,w,nxt;

}edge[MAXN];

int head[MAXN],num=;

inline void add_edge(int x,int y,int f,int z)

{

    edge[num].u=x;

    edge[num].v=y;

    edge[num].f=f;

    edge[num].w=z;

    edge[num].nxt=head[x];

    head[x]=num++;

}

int h[MAXN],dis[MAXN],PrePoint[MAXN],PreEdge[MAXN];

Pair Dij()

{

    int ansflow=,anscost=;

    while()

    {

        priority_queue<Pair>q;

        memset(dis,0xf,sizeof(dis));

        dis[S]=;

        q.push(make_pair(,S));

        while(q.size()!=)

        {

            Pair p=q.top();q.pop();

            if(-p.fi!=dis[p.se]) continue;

            if(p.se==T) break;

            for(int i=head[p.se];i!=-;i=edge[i].nxt)

            {

                int nowcost=edge[i].w+h[p.se]-h[edge[i].v];

                if(edge[i].f>&&dis[edge[i].v]>dis[p.se]+nowcost)

                {

                    dis[edge[i].v]=dis[p.se]+nowcost;

                    q.push(make_pair(-dis[edge[i].v],edge[i].v));

                    PrePoint[edge[i].v]=p.se;

                    PreEdge[edge[i].v]=i;

                }

            }

        }

        if(dis[T]>INF) break;

        for(int i=;i<=N;i++) h[i]+=dis[i];

        int nowflow=INF;

        for(int now=T;now!=S;now=PrePoint[now])

            nowflow=min(nowflow,edge[PreEdge[now]].f);

        for(int now=T;now!=S;now=PrePoint[now])

            edge[PreEdge[now]].f-=nowflow,

            edge[PreEdge[now]^].f+=nowflow;

        ansflow+=nowflow;

        anscost+=nowflow*h[T];

    }

    return make_pair(ansflow,anscost);

}

int main()

{

    #ifdef WIN32

    freopen("a.in","r",stdin);

    #endif

    memset(head,-,sizeof(head));

    N=read(),M=read(),S=read(),T=read();

    for(int i=;i<=M;i++)

    {

        int x=read(),y=read(),f=read(),z=read();

        AddEdge(x,y,f,z);

    }

    Pair ans=Dij();

    printf("%d %d",ans.fi,ans.se);

    return ;

}