Leetcode 230.二叉搜索树第k小的数

二叉搜索树第k小的数

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:

输入: root = [3,1,4,null,2], k = 1

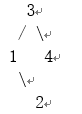
输出: 1

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3

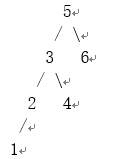
输出: 3

进阶：
如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化 kthSmallest 函数？

提示让用BST的性质来，那就是BST数值大小是：左<根<右，用中序遍历所有的节点就会得到一个有序数组，如果只求第k小的数，还可以用一个计数器记录已经遍历的节点数，只遍历到第k个节点返回即可。

 class Solution {

     List<Integer> list=new ArrayList<Integer>();
     public int kthSmallest(TreeNode root, int k) {
         IBTS(root);
         return list.get(k-1);
     }

     public void IBTS(TreeNode root){
         if(root==null) return;
         IBTS(root.left);
         list.add(root.val);
         IBTS((root.right));
     }
 }