poj 2104 K-th Number（主席树，详细有用）

poj 2104 K-th Number（主席树）

主席树就是持久化的线段树，添加的时候，每更新了一个节点的线段树都被保存下来了。

查询区间[L,R]操作的时候，只需要用第R棵树减去第L-1棵树就是区间[L,R]中增加的元素对应的树，然后查询这棵两棵树的差值对应的树就可以达到我们的目的。

每增加一个节点，必然有一条边被改变，那条边上的所有节点都会被改变。除这条边之外的其它节点用的是上一棵树的。

K-th Number

Time Limit: 20000MS		Memory Limit: 65536K
Total Submissions: 62232		Accepted: 21860
Case Time Limit: 2000MS

Description

You are working for Macrohard company in data structures department. After failing your previous task about key insertion you were asked to write a new data structure that would be able to return quickly k-th order statistics in the array segment. 
That is, given an array a[1...n] of different integer numbers, your program must answer a series of questions Q(i, j, k) in the form: "What would be the k-th number in a[i...j] segment, if this segment was sorted?" 
For example, consider the array a = (1, 5, 2, 6, 3, 7, 4). Let the question be Q(2, 5, 3). The segment a[2...5] is (5, 2, 6, 3). If we sort this segment, we get (2, 3, 5, 6), the third number is 5, and therefore the answer to the question is 5.

Input

The first line of the input file contains n --- the size of the array, and m --- the number of questions to answer (1 <= n <= 100 000, 1 <= m <= 5 000). 
The second line contains n different integer numbers not exceeding 10⁹ by their absolute values --- the array for which the answers should be given. 
The following m lines contain question descriptions, each description consists of three numbers: i, j, and k (1 <= i <= j <= n, 1 <= k <= j - i + 1) and represents the question Q(i, j, k).

Output

For each question output the answer to it --- the k-th number in sorted a[i...j] segment.

Sample Input

7 3
1 5 2 6 3 7 4
2 5 3
4 4 1
1 7 3

Sample Output

5
6
3

Hint

This problem has huge input,so please use c-style input(scanf,printf),or you may got time limit exceed.

Source

Northeastern Europe 2004, Northern Subregion

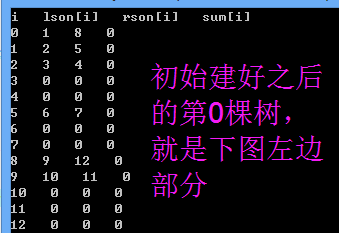
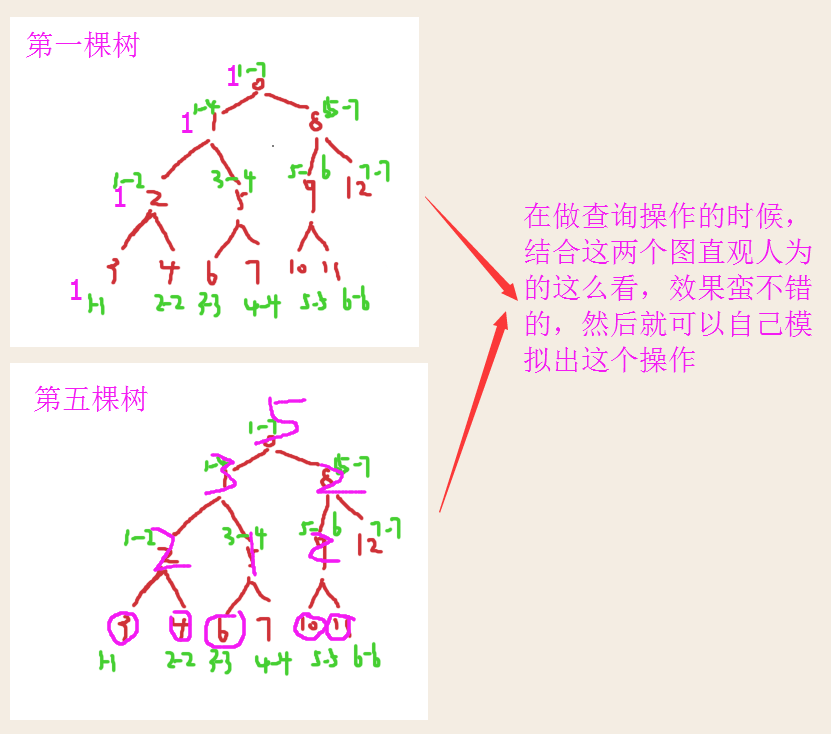
添加的这个节点离散化之后是1，也就是最左下角的那个节点。

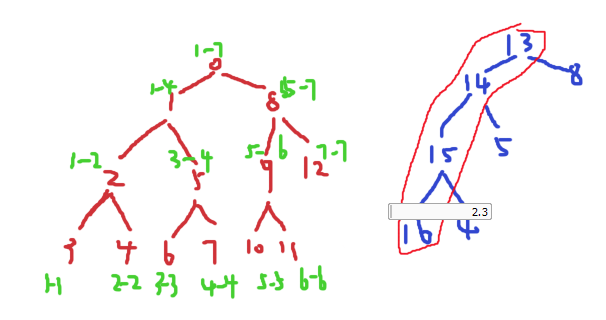
总共是7个数，离散化管它有几个不重复的数，按照最大情况7个个数来算就对了。

所以这7个数是依次会被放到这7个叶子节点上面的来。

数的序列是1 5 2 6 3 7 4

第一个数是1，离散化之后也是1，所以会被放到最左下角3那个位置，所以就是上图右边更新的情况，（注意看节点的下标）。

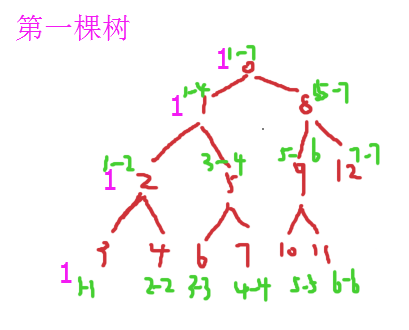
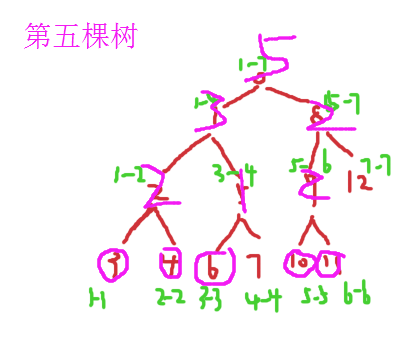
第5棵树根节点的左边有3个，第一棵树根节点左边只有一个，多3-1=2个，但是我要找的是3大的，所以必定在第五棵树减去第一颗树的右边的第一个。

测试代码（后面有AC代码）

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <vector>
 #include <algorithm>
 using namespace std;
 const int  MAXN = ;
 const int N = MAXN*;
 int n,m,q,tot;
 int T[MAXN],A[MAXN],t[MAXN];
 //详单于结构体
 int lson[N],rson[N],sum[N];
 vector<int>V;
 int getid(int x) //离散化
 {
     return lower_bound(V.begin(),V.end(),x)-V.begin()+;
 }
 int build(int l,int r)  //建立一棵空树
 {
     int rt = tot++;
     sum[rt] = ;//初始化，相当于初始化结构体中的sum元素
     //不是叶子节点
     if(l!=r){
         int mid=(l+r)>>;
         lson[rt] = build(l,mid);
         rson[rt] = build(mid+,r);
     }
     return rt;
 }

 //比如说第一组数是（0,1），表示继承的第0棵树，然后插入的那个数的id是1
 int update(int rt,int pos)  //把数组中的元素一次加入新的线段树中
 {
     int nrt = tot++;//相当于节点13
     int tmp = nrt;
     //sum[13]=sum[0]+1，这是插入第一个点的情况，表示sum[13]第一棵树比 sum[0]第0棵树多了一个元素
     sum[nrt]  = sum[rt]+;
     int l=,r=m;//相当于从根节点开始更新
     while(l<r) {//不停的从上往下（二分）去更新到那条路径的叶子节点
         int mid = (l+r)>>;
         //插入节点在线段树的左边
         if(pos<=mid) {
             lson[nrt] = tot++;//左边的节点就是我们新创建的这个节点，相当于节点14
             rson[nrt] = rson[rt];//右边节点就直接继承前一棵树 ，相当于节点8
             nrt = lson[nrt];//让13节点向下走到14号节点
             rt = lson[rt];//前一棵树继续往下走，把前一棵树0号节点的左孩子的值赋值给rt，方便让新的这棵树找得到5号节点，4号节点
             r = mid;//二分
         }else {
             rson[nrt] = tot++;
             lson[nrt] = lson[rt];//左边直接继承前一棵树
             nrt = rson[nrt];
             rt = rson[rt];
             l=mid+;
         }
         sum[nrt] = sum[rt]+;//节点在前一棵树的基础上面个数+1
     }
     return tmp;
 }

 //第y棵树减第x-1棵树就是xy之间的元素，然后找到第k大的即可
 //printf("%d\n",V[query(T[x-1],T[y],k)-1]);
 //相当于是在两棵树的差树的那颗树上面找
 int query(int lrt,int rrt,int k)
 {
     int l=,r=m;//从根节点开始找
     while(l<r) {//二分找
         int mid = (l+r)>>;
         int cnt = sum[lson[rrt]] - sum[lson[lrt]];//找到有多少个数目
         if(cnt>=k) {
             r = mid;
             lrt = lson[lrt];
             rrt = lson[rrt];
         } else {
             l = mid+;
             k-=cnt;//跑到右边去就要把左边的减掉
             lrt = rson[lrt];//第一棵树和第五课树都去右孩子，然后是找差值
             rrt = rson[rrt];
         }
     }
     return l;
 }
 //测试主席树
 void print(){
     cout<<"i"<<"   "<<"lson[i]"<<"   "<<"rson[i]"<<"   "<<"sum[i]"<<"   "<<endl;
     for(int i=;i<=*n;i++){
         cout<<i<<"   "<<lson[i]<<"   "<<rson[i]<<"   "<<sum[i]<<"   "<<endl;
     }
 }
 //测试T数组
 void printT(){
     cout<<"i"<<"   "<<"T[i]"<<"   "<<endl;
     for(int i=;i<=n;i++){
         cout<<i<<"   "<<T[i]<<"   "<<endl;
     }
 }
 int main()
 {
     freopen("in.txt","r",stdin);
     freopen("out.txt","w",stdout);
     //n个数q个操作
     scanf("%d%d",&n,&q);tot=;
     //A[i]存那些数
     for(int i=;i<=n;i++) {
         scanf("%d",&A[i]);
         V.push_back(A[i]);
     }
     sort(V.begin(),V.end());
     V.erase(unique(V.begin(),V.end()),V.end());
     //上面一部分是离散化
     m=V.size();//找到不重复的元素的个数
     cout<<m<<endl;

     T[] = build(,m);//建1到m的树
     cout<<"tot: "<<tot<<endl;
     print();
 //    cout<<T[0]<<endl;
     printT();
     for(int i=;i<=n;i++) {
         T[i] = update(T[i-],getid(A[i]));
         cout<<i<<"   "<<getid(A[i])<<endl;
     }
     printT();
     while(q--) {
         int x,y,k;
         scanf("%d%d%d",&x,&y,&k);
         //第y棵树减第x-1棵树就是xy之间的元素，然后找到第k大的即可
         //最后一个-1是因为V是从0开始
         printf("%d\n",V[query(T[x-],T[y],k)-]);
     }
     print();
     return ;
 }

AC代码

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <vector>
 #include <algorithm>
 using namespace std;
 const int  MAXN = ;
 const int N = MAXN*;
 int n,m,q,tot;
 int T[MAXN],A[MAXN],t[MAXN];
 int lson[N],rson[N],sum[N];
 vector<int>V;
 int getid(int x) //离散化
 {
     return lower_bound(V.begin(),V.end(),x)-V.begin()+;
 }
 int build(int l,int r)  //建立一棵空树
 {
     int rt = tot++;
     sum[rt] = ;
     if(l!=r){
         int mid=(l+r)>>;
         lson[rt] = build(l,mid);
         rson[rt] = build(mid+,r);
     }
     return rt;
 }

 int update(int rt,int pos)  //把数组中的元素一次加入新的线段树中
 {
     int nrt = tot++;
     int tmp = nrt;
     sum[nrt]  = sum[rt]+;
     int l=,r=m;
     while(l<r) {
         int mid = (l+r)>>;
         if(pos<=mid) {
             lson[nrt] = tot++;
             rson[nrt] = rson[rt];
             nrt = lson[nrt];
             rt = lson[rt];
             r = mid;
         }else {
             rson[nrt] = tot++;
             lson[nrt] = lson[rt];
             nrt = rson[nrt];
             rt = rson[rt];
             l=mid+;
         }
         sum[nrt] = sum[rt]+;
     }
     return tmp;
 }

 int query(int lrt,int rrt,int k)
 {
     int l=,r=m;
     while(l<r) {
         int mid = (l+r)>>;
         int cnt = sum[lson[rrt]] - sum[lson[lrt]];
         if(cnt>=k) {
             r = mid;
             lrt = lson[lrt];
             rrt = lson[rrt];
         } else {
             l = mid+;
             k-=cnt;
             lrt = rson[lrt];
             rrt = rson[rrt];
         }
     }
     return l;
 }
 int main()
 {//freopen("in.txt","r",stdin);
     scanf("%d%d",&n,&q);tot=;
     for(int i=;i<=n;i++) {
         scanf("%d",&A[i]);
         V.push_back(A[i]);
     }
     sort(V.begin(),V.end());
     V.erase(unique(V.begin(),V.end()),V.end());
     m=V.size();
     T[] = build(,m);
     for(int i=;i<=n;i++) {
         T[i] = update(T[i-],getid(A[i]));
     }
     while(q--) {
         int x,y,k;
         scanf("%d%d%d",&x,&y,&k);
         printf("%d\n",V[query(T[x-],T[y],k)-]);
     }
     return ;
 }