浅谈算法——splay

BST（二叉查找树）是个有意思的东西，种类巨TM多，然后我们今天不讲其他的，我们今天就讲splay

---

首先，如果你不知道Splay是啥，你也得知道BST是啥

如上图就是一棵优美的BST，它对于每个点保证其左子树内所有点小于自己，右子树内所有点大于自己，而且这棵树高只有\(\log n\)，所以找一个点只需要\(O(\log n)\)的时间

但是如果这个图长得极端一点就会变成这样……

这棵树就非常的不优美，每次查找的复杂度为\(O(n)\)，然后就\(O(n^2)\)了……

---

然后各种大佬们为了解决这个蓝瘦的事情，纷纷想出了一些解决方案，其中有个叫Tarjan的大佬，弄出了一个名叫Splay的玩意，然后我们来讲一下Splay的一些操作

---

1.旋转

旋转式BST（Splay是其中的一种）基本上都有此操作，不然不叫作旋转式，像fhqtreap那种非旋转式BST则没有该操作。网上大部分将旋转分为两个，ZIG与ZAG



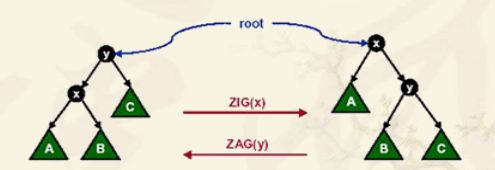
感觉这张图一点都不清楚。。。其实是我懒得画一张了

左边到右边的是ZIG(x)，右边到左边是ZAG(y)

ZIG和ZAG的结合也有几种情况





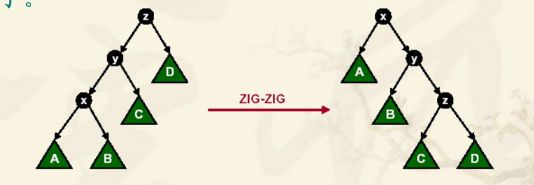
你发现它们这样转来转去，这棵树依然满足BST性质的，而且上图ZIG-ZAG操作中，还减少了树的高度，所以旋转式BST就是基于ZIG，ZAG以及组合操作，通过不断旋转自身来保证其树高，使得其非常优美

但是，写4个旋转实在是太麻烦了，于是我们将其简化为一个函数

首先我们需要明白，splay的旋转操作只会影响到3个点



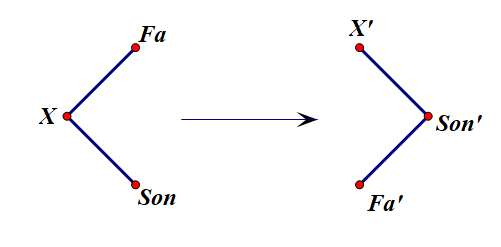
将x旋到根之后，其父亲和其儿子会如上图般变化，其他点都不会受到影响。那么这个旋转如何用一个函数来实现呢？

#define ls(x) tree[x][0]
#define rs(x) tree[x][1]
#define T(x) (rs(f[x])==x)
void move(int x){
	int fa=f[x],son=tree[x][T(x)^1];
	tree[x][T(x)^1]=fa;
	tree[fa][T(x)]=son;
	if (son)	f[son]=fa;
	f[x]=f[fa];
	if (f[x])   tree[f[x]][T(fa)]=x;
	f[fa]=x;
}

首先记录一下当前点的父亲，和其拐角后的儿子节点（先不管有没有父亲和儿子），然后将x的儿子改成fa，把fa的儿子改成son（记得改成拐角状）。

然后判断son是否存在，若存在，则f[son]=fa。

将x的父亲指向fa的父亲，不管fa的父亲是否存在（f[x]为零也可以）。

然后判断是否真正有f[x]（连边之后的父亲），如果有，那么将f[x]的儿子指向x，由于此时f[x]和fa的关系未断，因此可以直接用T(fa)，最后将fa的父亲指向x即可。

---

然后我们来看个有意思的东西

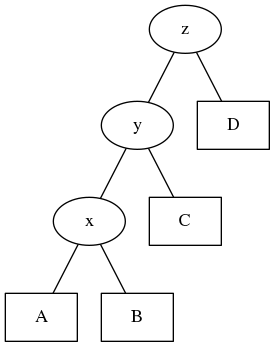
现在我们要把\(x\)旋到根上去，然后按照之前的旋转方法就有

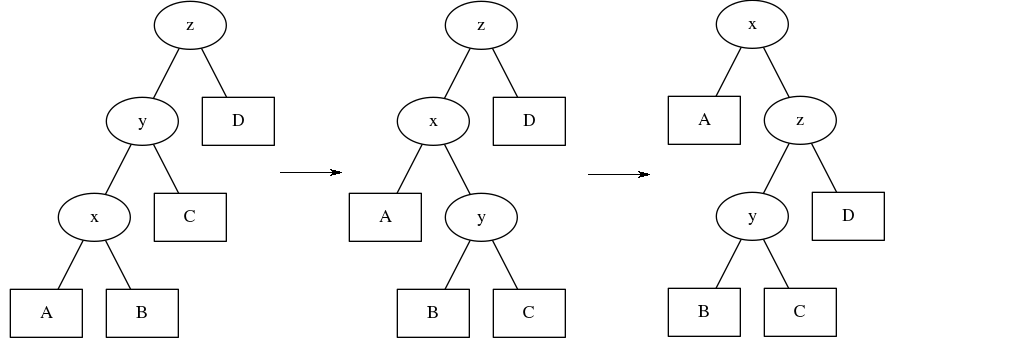
然后我们把图中的一条链标记出来

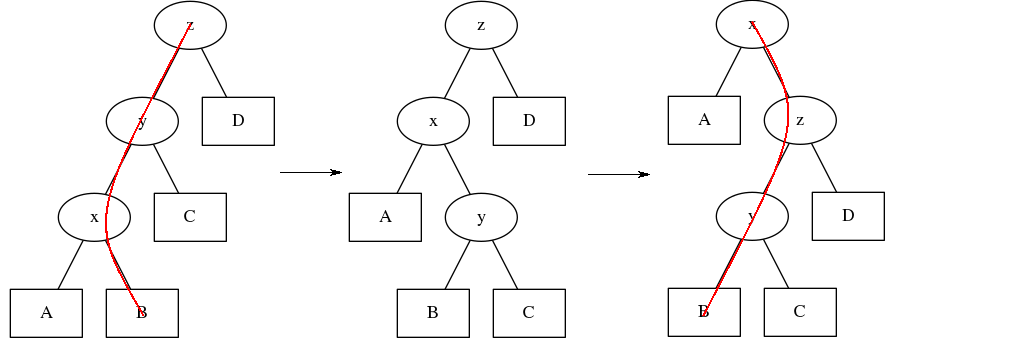
也就是说你只对着\(x\)旋转的话，很有可能被卡，所以我们就要进行一些优化，我们在旋转的时候进行讨论，如果x-y-z在同一直线上，我们就先旋y再旋x，否则直接旋x，这个方法就是双旋，代码实现也非常简单

一般来讲，单旋速度优于双旋，但容易被卡（你可以试着画一跳长链，然后分别用双旋和单旋将链底的点旋上来，然后看一下树的形态）

void splay(int x){
	while (f[x]){
		if (f[f[x]])	T(x)==T(f[x])?move(f[x]):move(x);
		move(x);
	}
	root=x;
}

Attention:move函数中的#define，对于之后的函数一直有效

---

2.插入

插入一个点的时候，从根节点找起，看要插入的点是要插在当前点的左边还是右边，如果要插在某一边且那一边刚好空着，就直接加进去即可，否则继续找。最后把插入的点splay到根，维护平衡

void insert(int x){
	val[++len]=x;
	if (!root){
		size[root=len]=1;
		return;
	}
	int i=root;
	while (true){
		size[i]++;
		if (x<=val[i]){
			if (!ls(i)){f[ls(i)=len]=i;break;}
			i=ls(i);
		}else{
			if (!rs(i)){f[rs(i)=len]=i;break;}
			i=rs(i);
		}
	}
	splay(len);
}

---

3.找前驱/后继

由于splay是一棵BST，因此找前驱的话，我们只需要找root的左儿子中，最右边的叶子节点；后继同理

int get_pre(){
	int x=ls(root);
	while (rs(x))   x=rs(x);
	return x;
}
int get_suc(){
	int x=rs(root);
	while (ls(x))   x=ls(x);
	return x;
}

---

4.查询

由于splay是棵二叉树，记录一下size之后便可以很容易找到排第k个的数是谁了

int find(int x,int i){
	if (!i) return 0;
	if (size[ls(i)]+1==x)   return i;
	if (x<=size[ls(i)])  return find(x,ls(i));
	return find(x-size[ls(i)]-1,rs(i));
}

---

5.删除

在通过某些特殊的方法得到需要删除的点的编号后（特殊方法什么的根据题意来），现将该点splay到根，如果左右儿子有一个空了，那么直接将那个没空的挪上来就好；否则就将其前驱/后继旋上来，然后判断一下x是new_root的左儿子还是右儿子，将x相应方向的儿子和new_root建立新的关系即可

void Delete(int x){
	splay(x);
	if (!(ls(x)&&rs(x))){
		f[root=ls(x)+rs(x)]=0;
		clear(x);
		return;
	}
	int i=get_pre();
	splay(i);
	size[f[rs(i)=rs(x)]=i]--;
	clear(x);
}

---

6.区间操作

多了区间操作的splay，为了防止越界，我们可以在最前面和最后面加上两个不动点，每次需要对区间[l,r]进行修改时，我们先把编号为l的点splay到根，再把编号为r+2的点splay到根，在旋的时候，l可能会变成r+2的孙子，我们把l单旋一下即可。这样子的话，l的左儿子就为我们需要求的那段区间了。



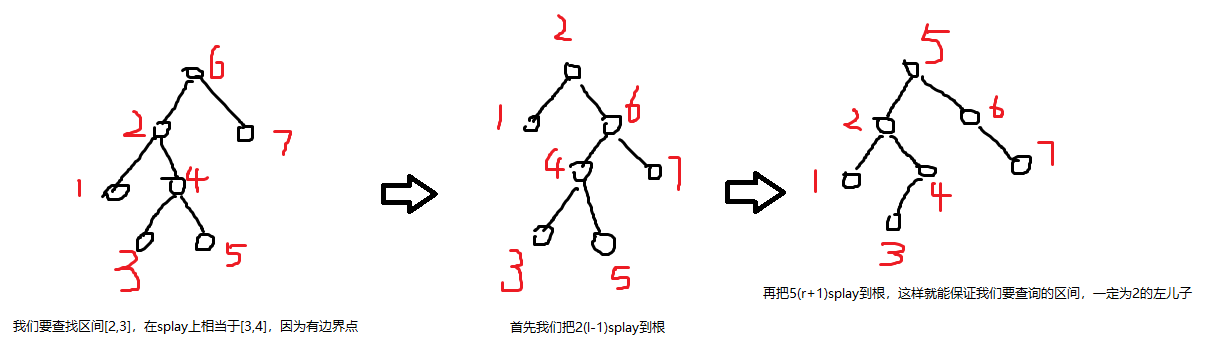
双旋的时候，2可能会变成5的孙子，那么我们把2单旋一下即可

---

splay的基本操作也就这些，下面我们来讲讲一个例题

例题

Tyvj 1728 普通平衡树

Description

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

Input

第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号(1<=opt<=6)

Output

对于操作3,4,5,6每行输出一个数，表示对应答案

Sample Input

10

1 106465

4 1

1 317721

1 460929

1 644985

1 84185

1 89851

6 81968

1 492737

5 493598

Sample Output

106465

84185

492737

HINT

1.n的数据范围：n<=100000

2.每个数的数据范围：[-2e9,2e9]

splay经典板子题，用到之前说的所有操作。删点的话，先找排名，然后找点删除。至于查询排名，由于BST的优美性质，所以判断一下往左右递归即可

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())  x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline void write(int x){
	if (x>=10)   write(x/10);
	putchar(x%10+'0');
}
const int N=1e5;
struct Splay{
	#define ls(x) tree[x][0]
	#define rs(x) tree[x][1]
	#define T(x) (rs(f[x])==x)
	int tree[N+10][2],f[N+10],size[N+10],val[N+10],root,len;
	void updata(int x){size[x]=size[ls(x)]+size[rs(x)]+1;}
	void clear(int x){f[x]=size[x]=ls(x)=rs(x)=0;}
	void move(int x){
		int fa=f[x],son=tree[x][T(x)^1];
		tree[x][T(x)^1]=fa;
		tree[fa][T(x)]=son;
		if (son)	f[son]=fa;
		f[x]=f[fa];
		if (f[x])   tree[f[x]][T(fa)]=x;
		f[fa]=x;
		updata(fa),updata(x);
	}
	void splay(int x){
		while (f[x]){
			if (f[f[x]])	T(x)==T(f[x])?move(f[x]):move(x);
			move(x);
		}
		root=x;
	}
	int get_pre(){
		int x=ls(root);
		while (rs(x))   x=rs(x);
		return x;
	}
	int get_suc(){
		int x=rs(root);
		while (ls(x))   x=ls(x);
		return x;
	}
	void Delete(int x){
		splay(x);
		if (!(ls(x)&&rs(x))){
			f[root=ls(x)+rs(x)]=0;
			clear(x);
			return;
		}
		int i=get_pre();
		splay(i);
		size[f[rs(i)=rs(x)]=i]--;
		clear(x);
	}
	void insert(int x){
		val[++len]=x;
		if (!root){
			size[root=len]=1;
			return;
		}
		int i=root;
		while (true){
			size[i]++;
			if (x<=val[i]){
				if (!ls(i)){f[ls(i)=len]=i;break;}
				i=ls(i);
			}else{
				if (!rs(i)){f[rs(i)=len]=i;break;}
				i=rs(i);
			}
		}
		splay(len);
	}
	int find(int x,int i){
		if (!i) return 0;
		if (size[ls(i)]+1==x)   return i;
		if (x<=size[ls(i)])  return find(x,ls(i));
		return find(x-size[ls(i)]-1,rs(i));
	}
	int get_rank(int x){
		int res=0;
		for (int i=root;i;) val[i]<x?res+=size[ls(i)]+1,i=rs(i):i=ls(i);
		return res+1;
	}
	void DELETE(int x){Delete(find(get_rank(x),root));}
	void GETRANK(int x){printf("%d\n",get_rank(x));}
	void RANK_GET(int x){printf("%d\n",val[find(x,root)]);}
	void GET_PRE(int x){printf("%d\n",val[find(get_rank(x)-1,root)]);}
	void GET_SUC(int x){printf("%d\n",val[find(get_rank(x+1),root)]);}
}Tree;
int main(){
	int n=read();
	for (int i=1;i<=n;i++){
		int flag=read(),x=read();
		if (flag==1)	Tree.insert(x);
		if (flag==2)	Tree.DELETE(x);
		if (flag==3)	Tree.GETRANK(x);
		if (flag==4)	Tree.RANK_GET(x);
		if (flag==5)	Tree.GET_PRE(x);
		if (flag==6)	Tree.GET_SUC(x);
	}
	return 0;
}