idea 解决git更新冲突

转载请注明出处：

　　对使用idea工具解决git冲突，最近有发现不同的解决冲突的方法，都很快捷方便，记录一下。

　　1.先commit 再pull，然后手动进行merge

　　

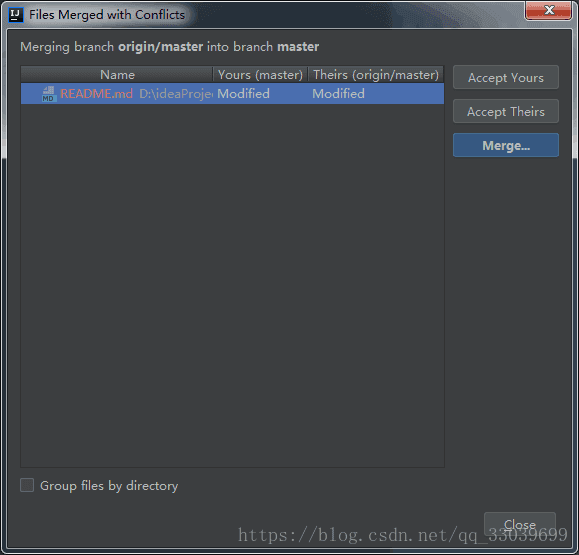
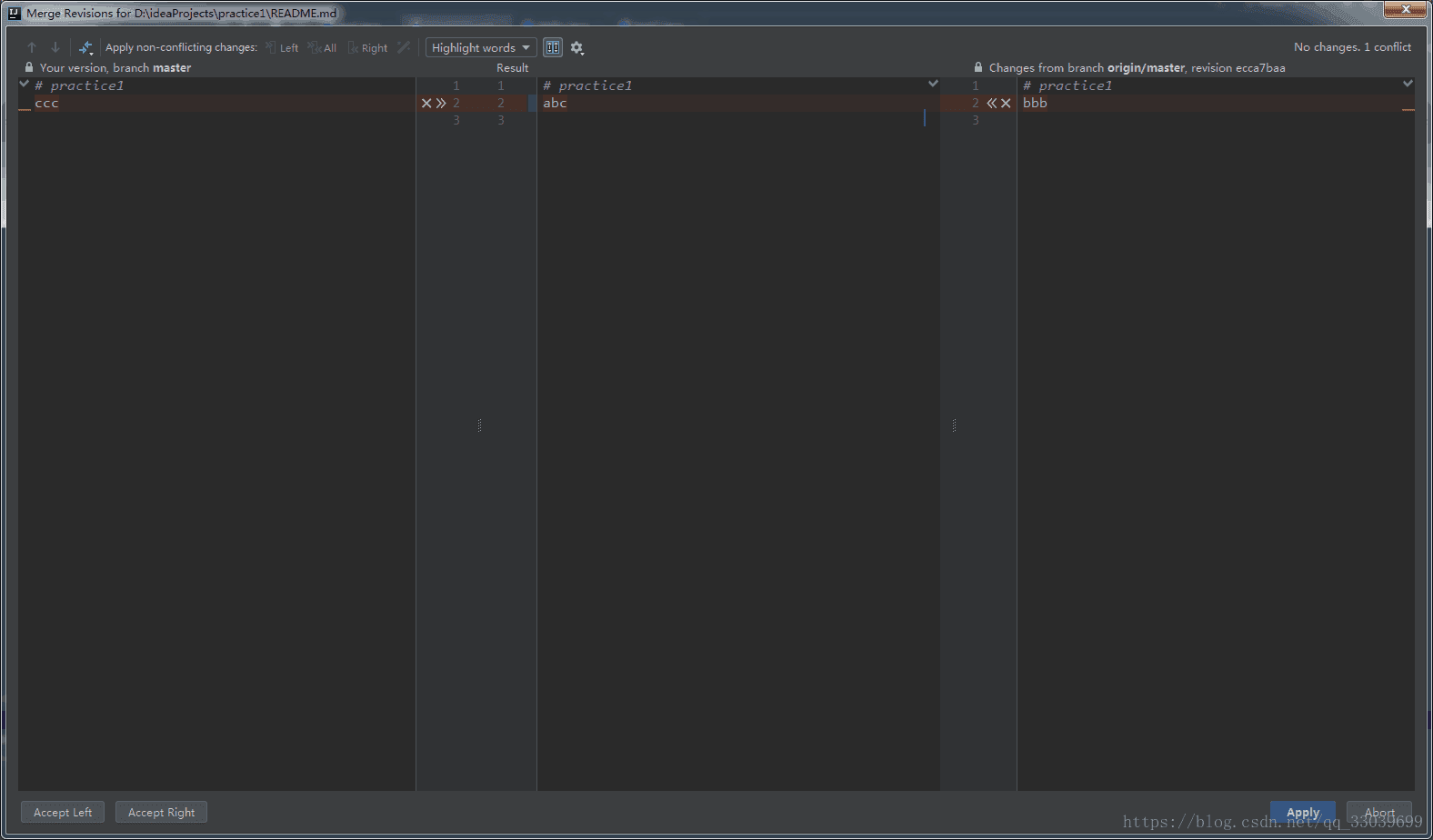
左边部分是本地仓库的代码，右边部分是远程仓库的代码，中间的result就是修改解决冲突之后的结果，点击箭头可以控制代码移动。

在result中修改好自己想要merge代码，然后点击apply。

点yes，这样就解决了冲突，解决完冲突后记得要commit一次，分别更新本地和远程仓库的代码。

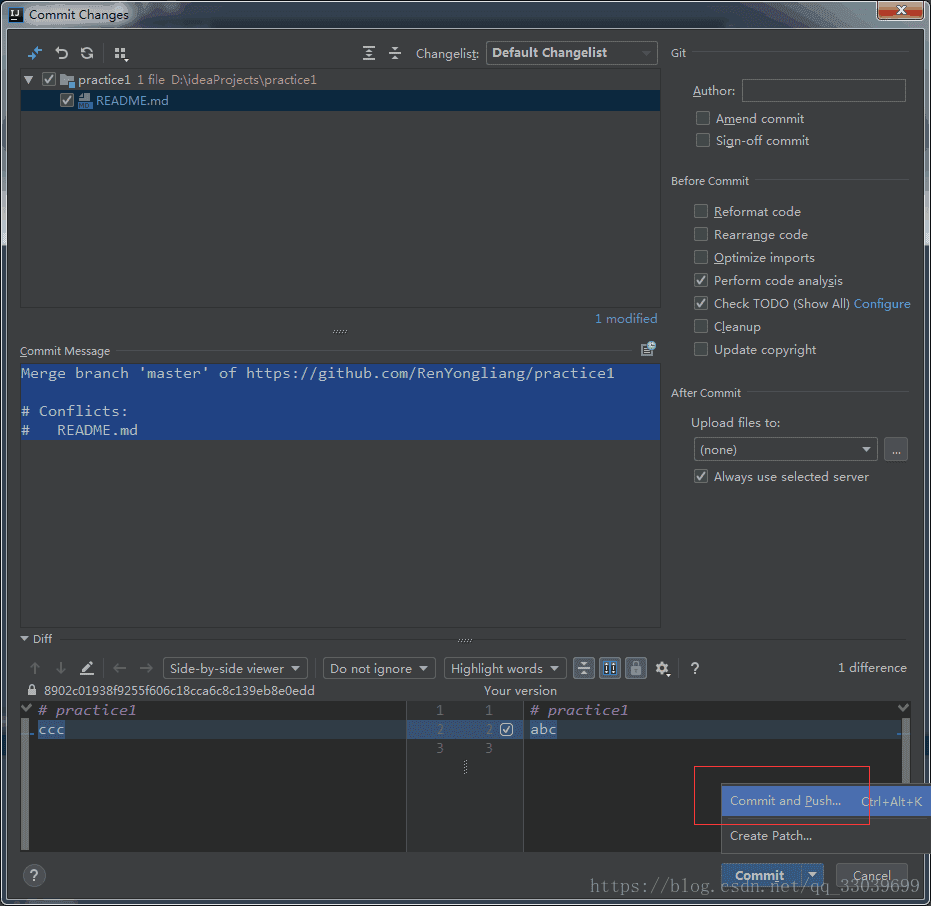
选择commit and push，点击push即可完成冲突解决和提交。

2.使用 stash 先保存本地更改，再使用 pull 同步git远程仓库代码到本地，然后使用unstash之前保存的标签，

选择项目右键---Git---Repository--Stash Changes

项目右键--Git--Repository--pull 同步远程代码到本地。

然后使用项目右键----Git ---Repository---unstash changes,选择对应的标签，并apply stash.

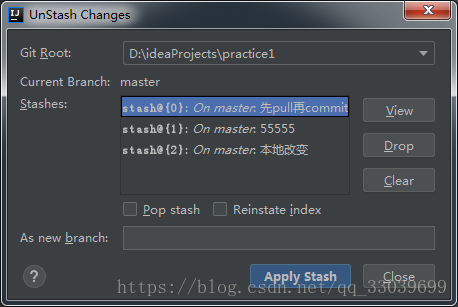
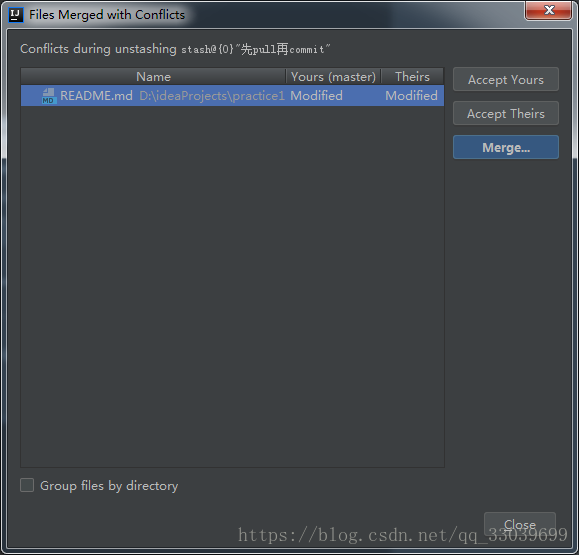
选择弹框中的冲突文件双击或Merge

此merge更改冲突方法如同第一步中的merge，解决冲突完成之后就可以commit and push.