CF1921F Sum of Progression 题解

题目链接：CF 或者洛谷

一道经典的类型题，把这种类型的题拿出来单独说一下。

注意到问题中涉及到需要维护 $a_{x+k\times step}$ 这样的信息，这样的信息很难用树型结构维护，比较容易用块级结构维护，我们注意到其实是每次这种步长 $+step$ 的信息很难维护，我们考虑一类特殊的分块：如果 $step$ 恰好为块长。

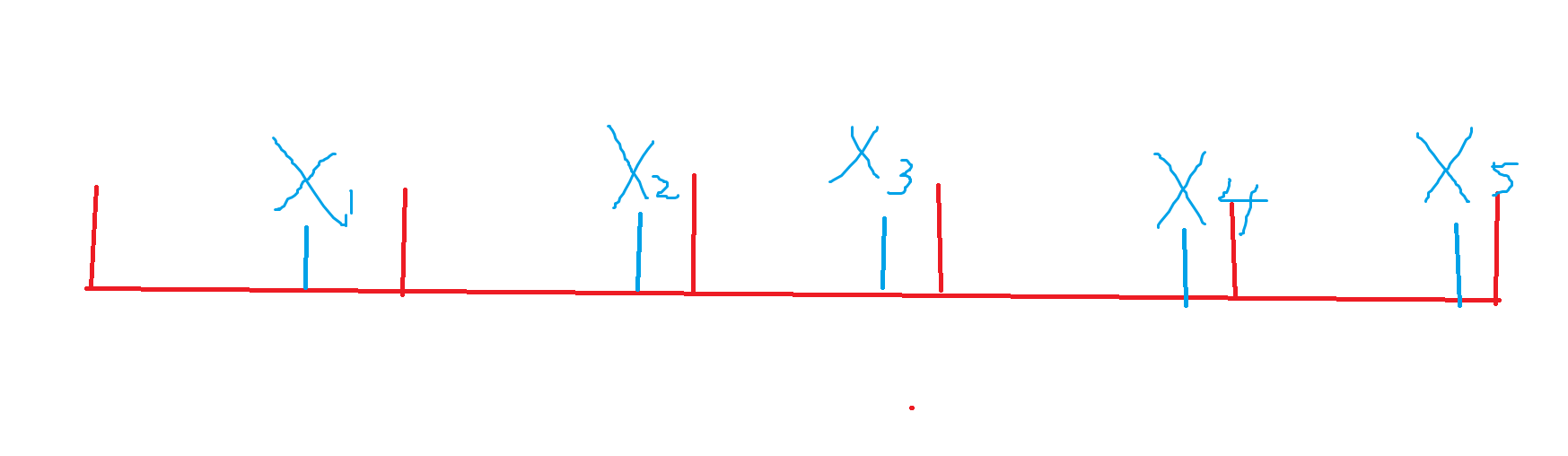
我们会惊讶地发现，从某个位置往后不断地走 $step$ 就是说不断地恰好跨过一个块长，它的路径上的每个点的信息在块里都是同一个位置，这样一来其实我们可以为每一种块长分块的结果维护它特有的一些信息。

注意到一点，在预处理时，每一种块长如果我们都暴力的情况下，从小块长开始，比如从块长为 $1$ 开始，显然处理的复杂度是 $O(n)$，这样一来，其实我们能处理最多 $\sqrt{n}$ 种块长，预处理的复杂度最多为 $n\sqrt{n}$，如果更长的块长我们注意到，如果暴力地从 $1$ 位置开始跳，那么最多也就跳 $\sqrt{n}$ 次，此时每个 $\ge \sqrt{n}$ 的块长其实是都是能直接暴力处理，这启发我们使用根号分治解决这类问题：

$块长 < \sqrt{n}$，考虑为这类所有块长分块维护统一的信息。
$块长 \ge \sqrt{n}$，考虑直接暴力。

这就是这类问题的模版框架。如果出现修改，我们对于查询的调整可能发生调整，比如有时候查询的是具体的值，那么可以考虑每种块长的贡献即可，最后会给出例题。

回到本题，我们需要对小块长维护怎样的信息，考虑到查询直接维护 $a_i \times 当前查询中的下标$ 是困难的，注意到阿贝尔求和的方式，我们可以把它拆成若干个前缀和做差的方式：

\[
a_{s}\times 1+a_{s+d}\times 2+a_{s+2d}\times 3+a_{s+3d} \times 4....a_{s+(k-1)\times d}\times k
\]

先考虑简单情形：

如果 $d==1$：

\[上式=a_s+2\times a_{s+1}+3\times a_{s+2}....k \times a_{s+k-1}
\]

类似于阿贝尔求和假如知道：

\[pre[x]=a_{1}+....a_s+a_{s+1}+a_{s+2}+....a_{x}
\]

那么很显然有原式子拆成如下图求和：

可以看出每一行都是一个区间和，借助前缀和，不妨设当前查询的最后一个数为 $end$：

\[ 原式=(pre[end]-pre[s-1])+(pre[end]-pre[s-2])+.....(pre[end]-pre[end-1])
\]

\[=k\times pre[end]-(pre[s-1]+pre[s-2]....pre[end-1])
\]

很容易看出，前面其实就为一个前缀和，后面则是“前缀和数组”的区间和形式，显然维护前缀和数组的前缀和就能办到了。

现在抽象一下，如果 $d \neq 1$，怎么解决：

事实上，我们把上式改写一下：

\[pre[d][idx]=a_{start}+a_{start+d}+a_{start+2d}+....a_{idx}
\]

其中 $start$ 为从 $idx$ 往前不断走 $d$ 长度能达到的最早起点，换句话来说，就是最开始我们提到的那张图：

$idx$ 此时可能不位于第一个块处，比如 $idx=x_2$，那么 $x_1$ 就是它在第一个块的相对位置，也即是 $start$，我们维护的就是这一步所有 $x$ 之和。

那么上面的式子显然可以改写为：

\[k\times pre[end]-(pre[s-d]+pre[s]+pre[s+d]+pre[s+2d]....pre[end-d])
\]

这里的 $pre$ 第一维取 $d$，省略第一维为上述形式。那么我们可以维护两个数组：

$pre[d][idx]$ 表示 $d$ 长度的块的这些 $x$ 的前缀和信息。
$Prepre[d][idx]$ 表示 $d$ 长度的这些 $pre[d][idx]$ 的前缀和信息。

其中易知道 $Prepre[d][idx]=pre[d][start]+pre[d][start+d].....pre[d][idx]$。

那么上述式子就可以轻易改写了：

\[=k \times pre[d][end]-(Prepre[d][end-d]-Prepre[d][s-2\times d])
\]

其实只需要注意到，前缀和作差中后一项不再是 $-1$，改为 $-d$ 即可。

最后的细节

注意到有类似 $s-2\times d$ 这类下标，我们最好和 $0$ 取个 $max$，防止出现负数，究其原因可能这个块就是第一项了。然后注意到块比较小的时候，如果 $k$ 比较小也可以暴力，那么我们可以对这两类情况同时走暴力分支也行。当然改写成后缀和也是可以的，不用怎么需要考虑越界问题，因为超过的部分你数组开大点直接能取值为 $0$ 的后缀和了。记得多测情空。

带注释参考代码

#include <bits/stdc++.h>

// #pragma GCC optimize("Ofast,unroll-loops")

// #pragma GCC optimize(2)

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/tree_policy.hpp>

#include <ext/pb_ds/trie_policy.hpp>

#include <ext/pb_ds/tag_and_trait.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/list_update_policy.hpp>

#include <ext/pb_ds/assoc_container.hpp>

#include <ext/pb_ds/exception.hpp>

#include <ext/rope>

#endif

using namespace std;

using namespace __gnu_cxx;

using namespace __gnu_pbds;

typedef long long ll;

typedef long double ld;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

typedef tuple<int, int, int> tii;

typedef tuple<ll, ll, ll> tll;

typedef unsigned int ui;

typedef unsigned long long ull;

typedef __int128 i128;

#define hash1 unordered_map

#define hash2 gp_hash_table

#define hash3 cc_hash_table

#define stdHeap std::priority_queue

#define pbdsHeap __gnu_pbds::priority_queue

#define sortArr(a, n) sort(a+1,a+n+1)

#define all(v) v.begin(),v.end()

#define yes cout<<"YES"

#define no cout<<"NO"

#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);

#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);

#define forn(i, a, b) for(int i = a; i <= b; i++)

#define forv(i, a, b) for(int i=a;i>=b;i--)

#define ls(x) (x<<1)

#define rs(x) (x<<1|1)

#define endl '\n'

//用于Miller-Rabin

[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>

int disc(T* a, int n)

{

    return unique(a + 1, a + n + 1) - (a + 1);

}

template <typename T>

T lowBit(T x)

{

    return x & -x;

}

template <typename T>

T Rand(T l, T r)

{

    static mt19937 Rand(time(nullptr));

    uniform_int_distribution<T> dis(l, r);

    return dis(Rand);

}

template <typename T1, typename T2>

T1 modt(T1 a, T2 b)

{

    return (a % b + b) % b;

}

template <typename T1, typename T2, typename T3>

T1 qPow(T1 a, T2 b, T3 c)

{

    a %= c;

    T1 ans = 1;

    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;

    return modt(ans, c);

}

template <typename T>

void read(T& x)

{

    x = 0;

    T sign = 1;

    char ch = getchar();

    while (!isdigit(ch))

    {

        if (ch == '-')sign = -1;

        ch = getchar();

    }

    while (isdigit(ch))

    {

        x = (x << 3) + (x << 1) + (ch ^ 48);

        ch = getchar();

    }

    x *= sign;

}

template <typename T, typename... U>

void read(T& x, U&... y)

{

    read(x);

    read(y...);

}

template <typename T>

void write(T x)

{

    if (typeid(x) == typeid(char))return;

    if (x < 0)x = -x, putchar('-');

    if (x > 9)write(x / 10);

    putchar(x % 10 ^ 48);

}

template <typename C, typename T, typename... U>

void write(C c, T x, U... y)

{

    write(x), putchar(c);

    write(c, y...);

}

template <typename T11, typename T22, typename T33>

struct T3

{

    T11 one;

    T22 tow;

    T33 three;

    bool operator<(const T3 other) const

    {

        if (one == other.one)

        {

            if (tow == other.tow)return three < other.three;

            return tow < other.tow;

        }

        return one < other.one;

    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)

    {

    }

};

template <typename T1, typename T2>

void uMax(T1& x, T2 y)

{

    if (x < y)x = y;

}

template <typename T1, typename T2>

void uMin(T1& x, T2 y)

{

    if (x > y)x = y;

}

constexpr int N = 1e5 + 10;

constexpr int Size = ceil(sqrt(N));

constexpr int CNT = (N + Size - 1) / Size + 1;

int n, q;

ll a[N];

ll pre[CNT + 1][N];

ll Prepre[CNT + 1][N];

inline void solve()

{

    cin >> n >> q;

    forn(i, 1, n)cin >> a[i];

    int siz = sqrt(n);

    forn(i, 1, siz)

    {

        forn(j, 1, n)

        {

            pre[i][j] = a[j];

            if (j > i)pre[i][j] += pre[i][j - i];

            Prepre[i][j] = pre[i][j];

            if (j > i)Prepre[i][j] += Prepre[i][j - i];

        }

    }

    forn(i, 1, q)

    {

        ll s, d, k;

        cin >> s >> d >> k;

        ll ans = 0;

        if (k <= siz or d >= siz)forn(i, 1, k)ans += a[s + (i - 1) * d] * i;

        else

        {

            int end = s + (k - 1) * d;

            int endpre = end - d;

            ans = k * pre[d][end] - (Prepre[d][endpre] - Prepre[d][max(s - 2 * d, 0ll)]);

        }

        cout << ans << " ";

    }

    forn(i, 1, siz)forn(j, 1, n)pre[i][j] = Prepre[i][j] = 0;

    cout << endl;

}

signed int main()

{

    // MyFile

    Spider

    //------------------------------------------------------

    // clock_t start = clock();

    int test = 1;

    //    read(test);

    cin >> test;

    forn(i, 1, test)solve();

    //    while (cin >> n, n)solve();

    //    while (cin >> test)solve();

    // clock_t end = clock();

    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;

}

\[最终单个\ Test\ 的时间复杂度为预处理加若干次查询: O(n\sqrt{n}+q\sqrt{n})
\]

推荐经典题：P5309 [Ynoi2011] 初始化题解