【验证码逆向专栏】最新某验三代滑块逆向分析，干掉所有的 w 参数！

声明

本文章中所有内容仅供学习交流使用，不用于其他任何目的，不提供完整代码，抓包内容、敏感网址、数据接口等均已做脱敏处理，严禁用于商业用途和非法用途，否则由此产生的一切后果均与作者无关！

本文章未经许可禁止转载，禁止任何修改后二次传播，擅自使用本文讲解的技术而导致的任何意外，作者均不负责，若有侵权，请在公众号【K哥爬虫】联系作者立即删除！

前言

最近很多粉丝反馈，某验三代的滑块一直返回 forbidden，不知道为什么通过不了，尝试了很多方法都不行。其实是因为之前只校验了第三个 w 参数的值，现在官网加强了校验，前面两个 w 参数也需要逆出来，三个 w 参数相互关联，有一个不对，就无法通过验证。目前只发现官网做了更新，今后其他网站可能也会再上点强度。本文将会对每个 w 参数逐一逆向分析。

逆向目标

目标：最新某验 3 代滑块分析
网址：aHR0cHM6Ly93d3cuZ2VldGVzdC5jb20vZGVtby8=

抓包分析

刷新页面，通过抓包发现， register-slide 接口会返回 challenge 和 gt 值，为接口 get.php 的主要请求参数：

get.php 接口会返回 c 和 s，后面会用到，新版界面此接口里的 w 不可以置空，旧版则可以置空：

点击按键验证，会弹出滑块窗口，同时抓到了一个 ajax.php 接口，这个接口会返回验证码的类型，虽然没用，但是如果不请求或者请求不带 w 后面都会报错。旧版的话这个接口也是必须请求，但是 w 也是可以置空，且后面不会报错：

紧着着，我们要又抓到一个 get.php 接口，这个接口仍然给我们返回 c 和 s，请求不一样的是，这个接口里面还给我们返回滑块图片以及底图：

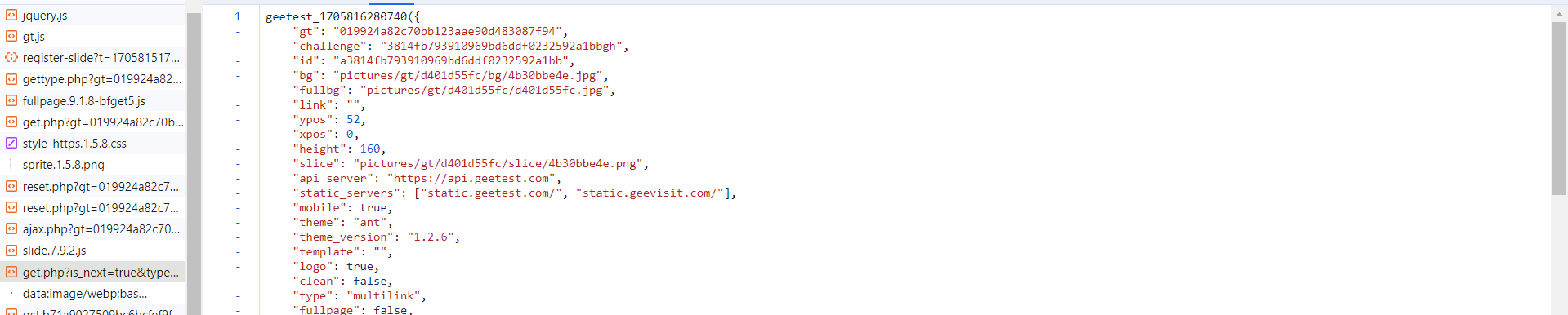
紧接着，我们滑动完成拼图，得到验证结果 validate 参数，这个参数就是后续登录的令牌，在后续操作的请求中会用到：

逆向分析

第一个 w

从 get.php 接口处跟栈，或者直接搜 "\u0077" 即可成功定位，w=i+r：

关键代码如下：

var r = t[$_CEFDY(1196)]()

o = $_BEH()[$_CEFCV(1127)](fe[$_CEFDY(431)](t[$_CEFCV(370)]), t[$_CEFDY(1143)]()) i = R[$_CEFDY(1197)](o)

很明显，这几个参数对于我们都不陌生了，我们进入 l 参数，发现 this[$_CGHDO(1143)](e) 为 16 位随机字符串将 new G()[$_CGHDO(93)] 这个函数扣一下即可，这里很明显，构造了一个 G 函数，所以我们只需要把 G 函数扣一下即可：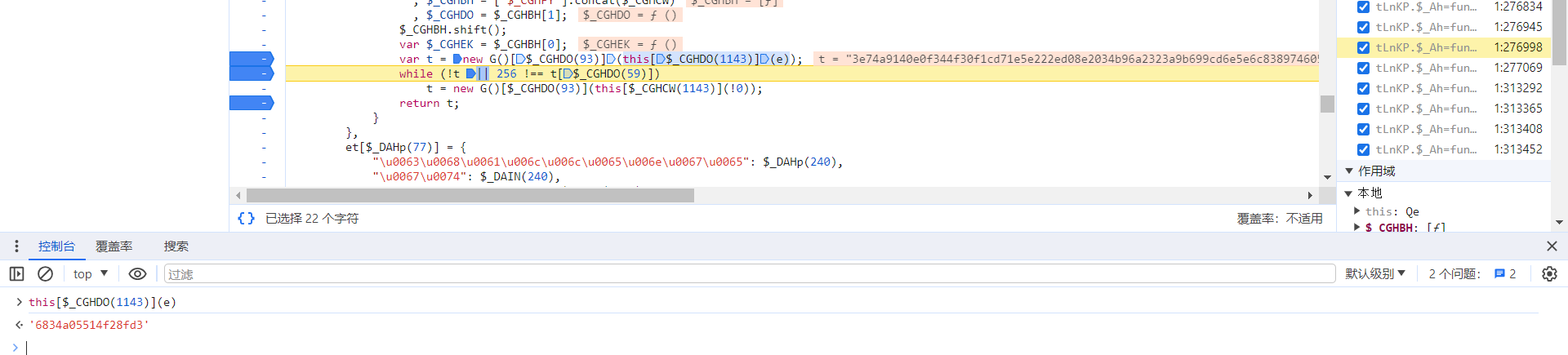

或者我们进入 G 的原型链 set_public 中，下断点，将他的 RSA 公钥和模值找到即可。所以 r 为 RSA 加密 16 位随机字符串。至此 r 值已经分析完毕。

接下来是 o 值，加密方法为 $_BEH()[$_CEFCV(1127)]，传入参数为 t[$_CEFDY(1143)]() 和 fe[$_CEFDY(431)](t[$_CEFCV(370)])。我们发现 t[$_CEFDY(1143)]() 为 rsa 加密的 key，t[$_CEFDY(1143)]() 和 fe[$_CEFDY(431)](t[$_CEFCV(370)]) 为明文参数。进入加密方法，打断点调试，我们发现是 AES 加密，同时初始向量是 0000000000000000：

直接扣代码，或者引库复现即可：

function Aes_encrypt(text, key_value) {

    var key = CryptoJS.enc.Utf8.parse(key_value);

    var iv = CryptoJS.enc.Utf8.parse("0000000000000000");

    var srcs = CryptoJS.enc.Utf8.parse(text);

    var encrypted = CryptoJS.AES.encrypt(srcs, key, {

        iv: iv,

        mode: CryptoJS.mode.CBC,

        padding: CryptoJS.pad.Pkcs7

    });

    for (var r = encrypted, o = r.ciphertext.words, i = r.ciphertext.sigBytes, s = [], a = 0; a < i; a++) {

        var c = o[a >>> 2] >>> 24 - a % 4 * 8 & 255;

        s.push(c);

    }

    return s;

}

现在，我们来分析一下明文的关键参数，这里我们采用 K 哥工具站，来解析一下，关键参数如下：

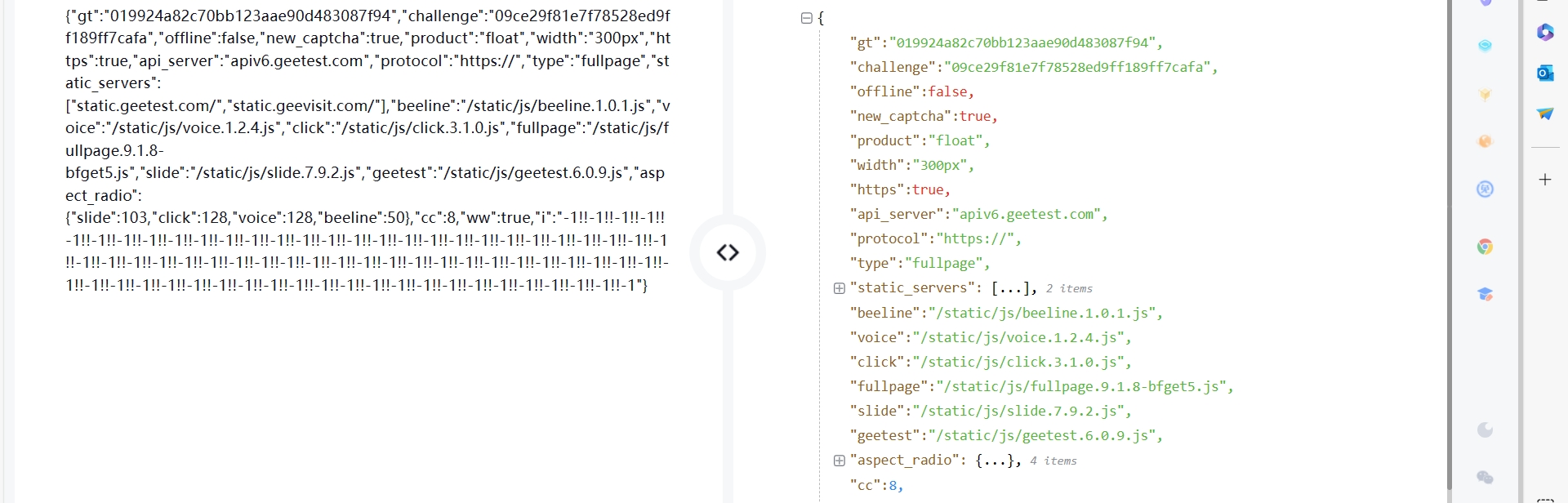
gt，challenge：第一个接口 /register-slider 返回；
offline， static_servers ： static_servers 其他参数固定即可。

至此我们 o 就分析完毕，终于只剩下一个 i 值，接下来我们分析一下 i 值，我们进入 R[$_CEFDY(1197)] 函数，发现 i 值为 t 中的俩个 value 值相加，t 的定义在断点上方：

传入的参数 e 为我们上一个步骤 aes 加密后的值，跟进到 this[$_IJDN(480)] 中，我们发现他属于 m 模块下的函数：

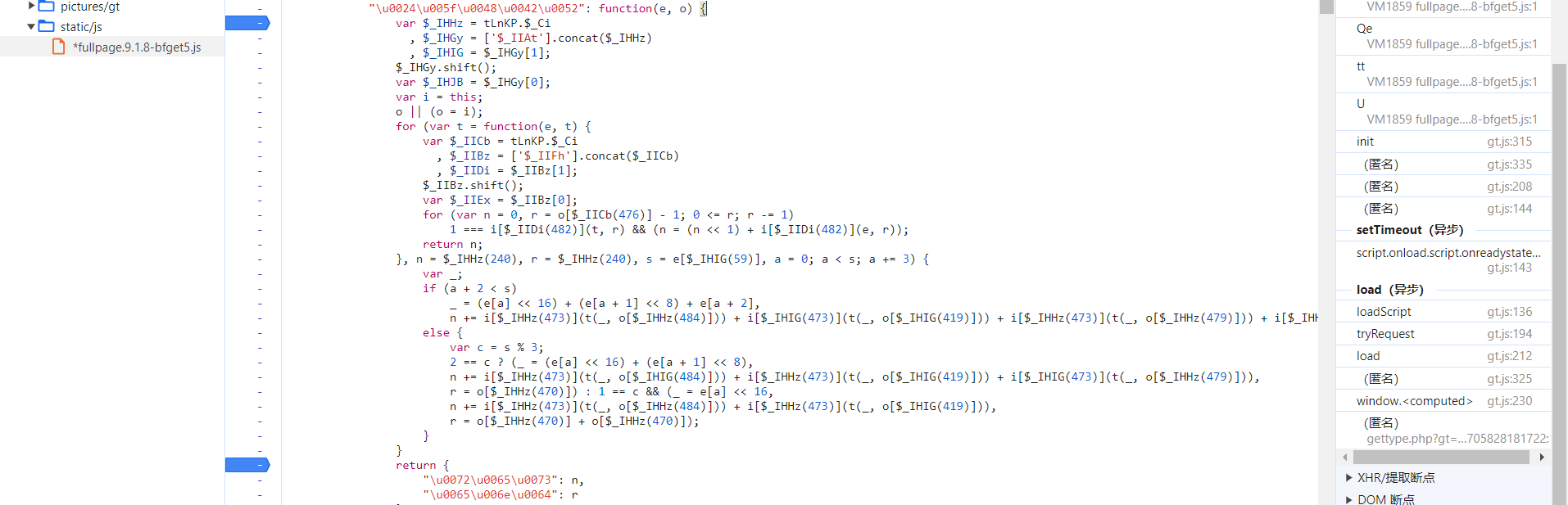
将整个 m 扣下来，复现如下：

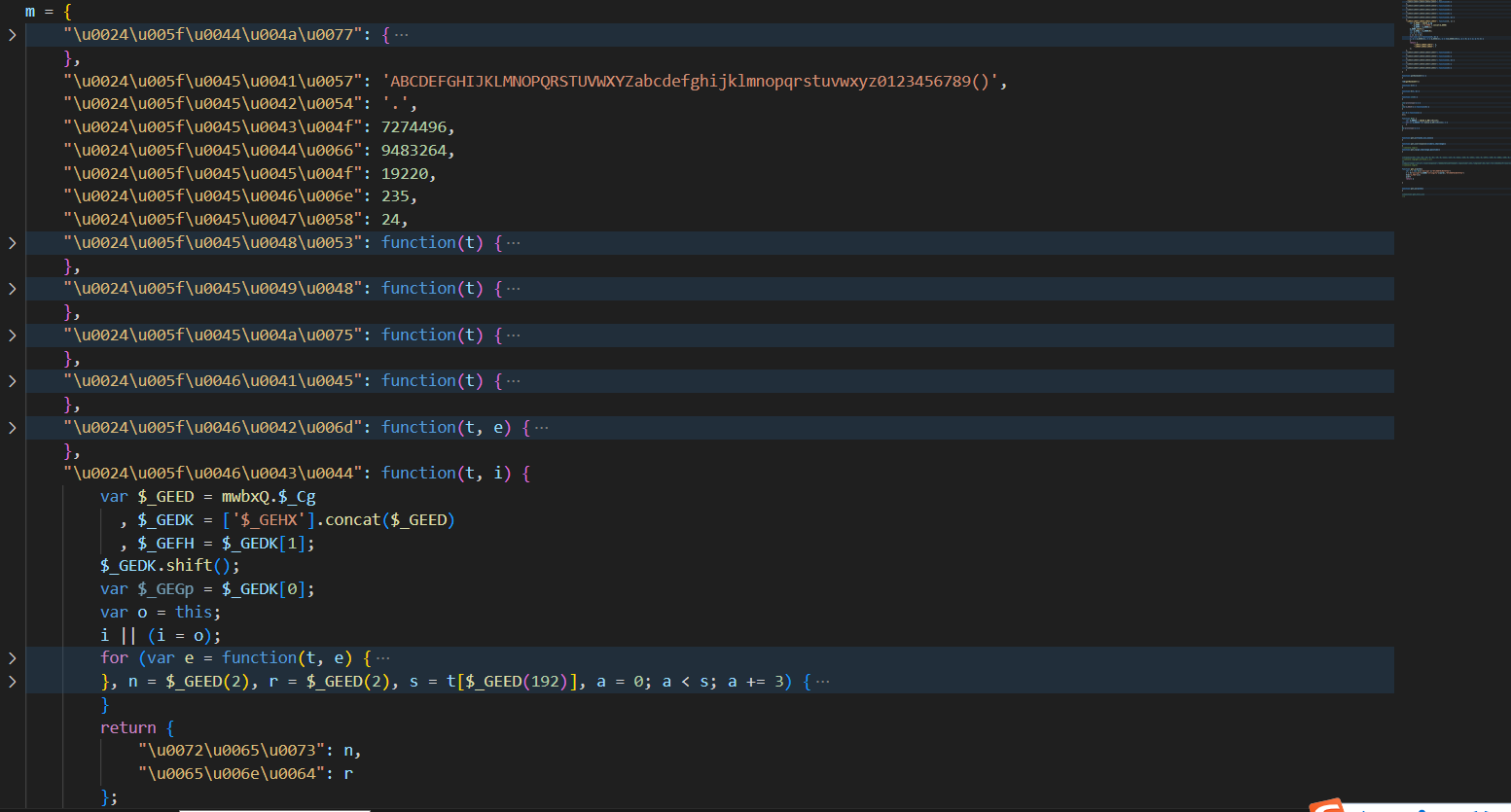
小结：第一个 w 和以前扣法基本一致，只是明文上有参差之分。

第二个 w

目前，我们第一个接口已经完成，拿到了返回的 s 和 c，接下来我们进入 ajax.php 接口，还是跟栈进入。

我们依然搜索定位参数"\u0077" ，发现并没有搜到，所以这个 w 和我们以前的扣法有点不一样！！！不过通过，跟栈的方式，我们找到正确位置。位置的话在 var n = {}; 这个地方，我们下断点：

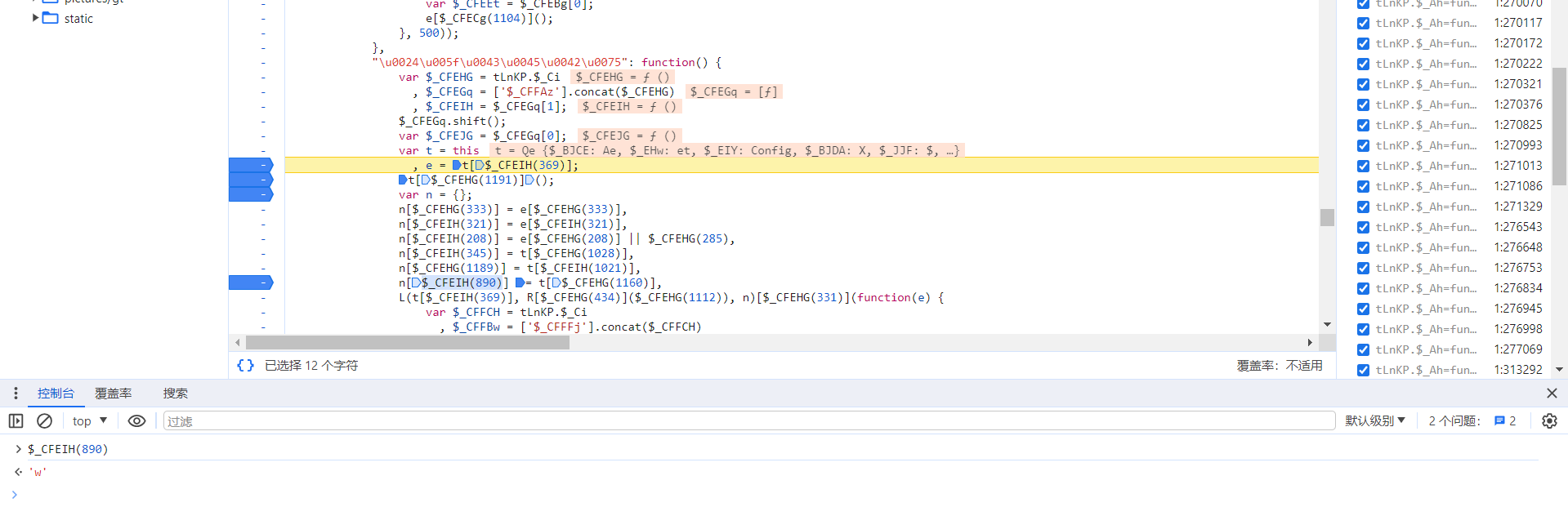
w 值就是 t[$_CFEHG(1160)]，前面我们发现 var t=this，然后经过 t[$_CFEHG(1191)]()，我们的 w 值就生成了。我们进入这个函数之中，进入以后发现异常的熟悉，这不就是无感系列的 w 吗？

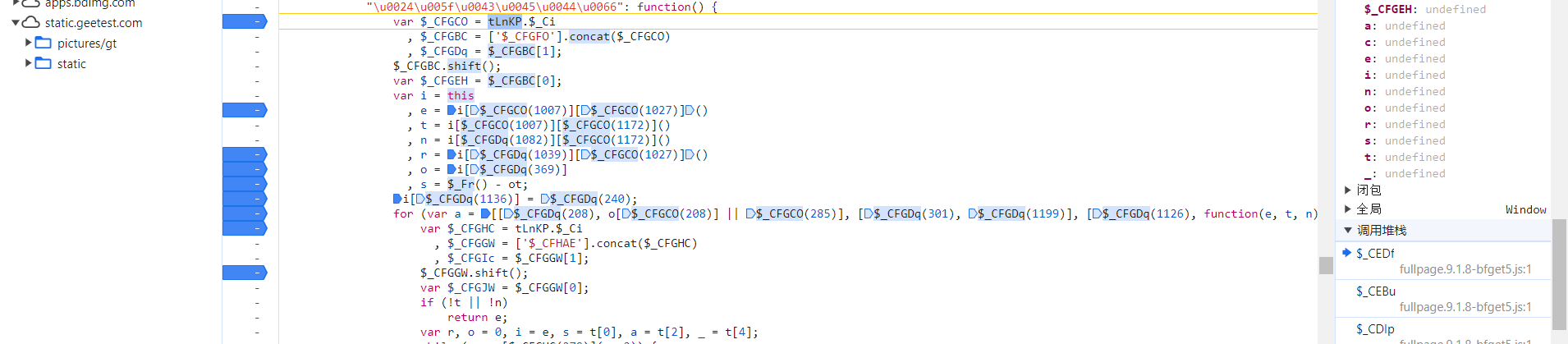
当然如果你是第一次扣，也不要心急，我们找到 w 定位的地方：

i[$_CFHIs(1160)] = R[$_CFHIs(1197)](c[$_CFHIs(93)](r, i[$_CFHIs(1143)]()))

我们简单修改一下代码，大概如下 w=R["encrypt"](r,key)，没错这个 R 方法其实与第一个 w 中 i 生成方式一样。所以现在，我们只需要解决 r 参数就可以完成第二个 w 的逆向。我们看一下 r 参数包括那些，我们依旧使用 K 哥工具站进行解析：

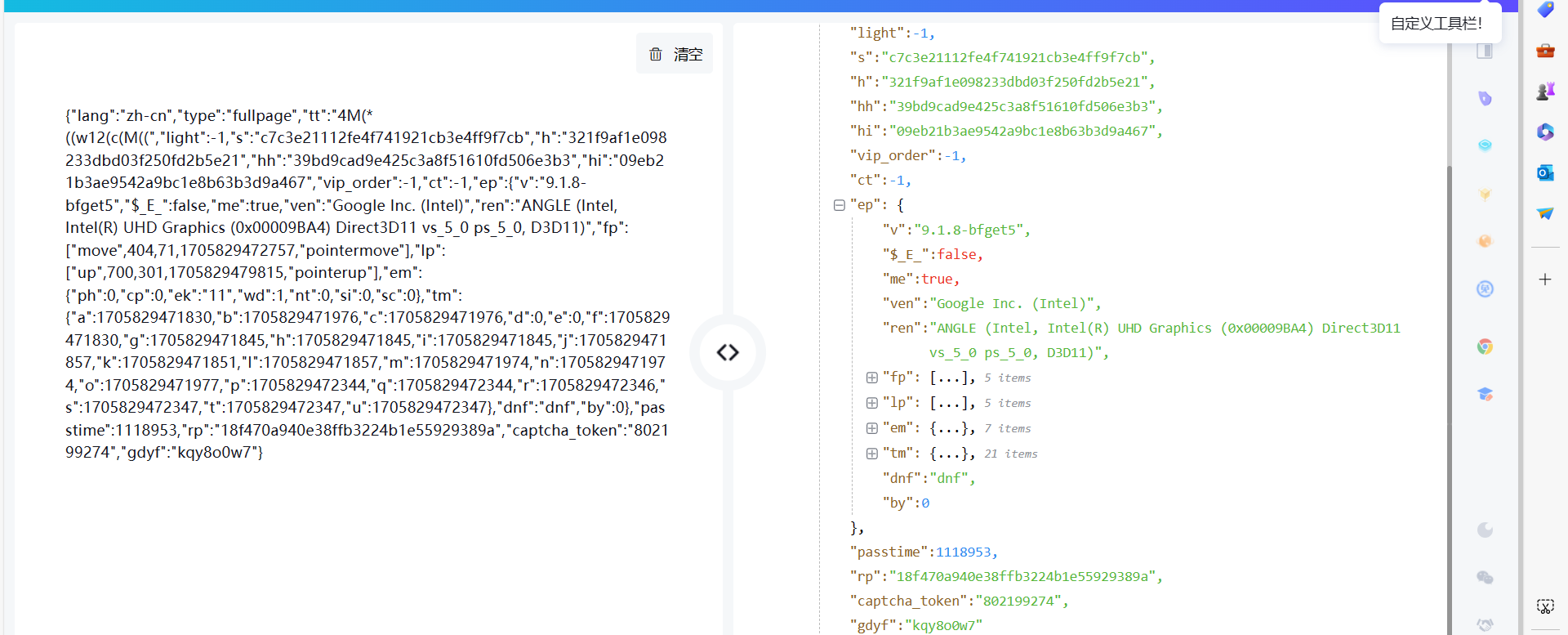
nr = {

    "lang": "zh-cn",

    "type": "fullpage",

    "tt": "M3*8Pjp8Pj9HbUp8PN9U),,:A(,(5(,(m-BJBFB:bgfA9/1O6*:I:JkNjRj31RkK**2KDRjE1S0OMM9*)-2.k6h)).E-:-)-9-:(:5b9-:1Mal2UK1RjY1I****)*:F3)pM0/JBBBA(((((,((iB9(((((,(5bn)BBBo95(,(qcjc*)R)fM2*QWU3cUA.N9?-G5N(:(?-N6,B1-2OUS_M9b?M:(A-)19d_cUS/BTF@AfC*Mf5?M95U-)1E1*OE(mj@.NQJ2@(g5@Acb?T)0N5u9khbE6,:CX)*E/B5-*Mb*)ME-((((M(((((((Lqqqp(Df((((((bb55,55(5((,((n-.(--88e(qR@).?2WE-Q(c19M9-)M919/)MM/)(P-U-(/)M*/.M*-)4)M@-N9d5Y-,-d(?b9/,M1AB9*nF)2(J*Df*M9/)MfN9*)(UU(0)(N1I-*b9/)(0qqM)qqp(-n",

    "light": "SPAN_0",

    "s": "c7c3e21112fe4f741921cb3e4ff9f7cb",

    "h": "321f9af1e098233dbd03f250fd2b5e21",

    "hh": "39bd9cad9e425c3a8f51610fd506e3b3",

    "hi": "09eb21b3ae9542a9bc1e8b63b3d9a467",

    "vip_order": -1,

    "ct": -1,

    "ep": {

        "v": "9.1.8-bfget5",

        "$_E_": false,

        "me": true,

        "ven": "Google Inc. (Intel)",

        "ren": "ANGLE (Intel, Intel(R) HD Graphics 520 Direct3D11 vs_5_0 ps_5_0, D3D11)",

        "fp": ["move", 483, 149, 1702019849214, "pointermove"],

        "lp": ["up", 657, 100, 1702019852230, "pointerup"],

        "em": {"ph": 0, "cp": 0, "ek": "11", "wd": 1, "nt": 0, "si": 0, "sc": 0},

        "tm": {

            "a": 1702019845759,

            "b": 1702019845951,

            "c": 1702019845951,

            "d": 0,

            "e": 0,

            "f": 1702019845763,

            "g": 1702019845785,

            "h": 1702019845785,

            "i": 1702019845785,

            "j": 1702019845845,

            "k": 1702019845812,

            "l": 1702019845845,

            "m": 1702019845942,

            "n": 1702019845946,

            "o": 1702019845954,

            "p": 1702019846282,

            "q": 1702019846282,

            "r": 1702019846287,

            "s": 1702019846288,

            "t": 1702019846288,

            "u": 1702019846288

        },

        "dnf": "dnf",

        "by": 0

    },

    "passtime": 5365,

    "rp": "0d51406b2c658811294a91e9ea533bed",

    "captcha_token": "541381339",

    "gdyf": "kqy8o0w7"

}

很明显，这里面有很多参数，一眼看起来很多参数像 md5 加密，我们向上调试进行分析，就可以找到参数定义的地方。这里的 e，t，n，t 是浏览器环境的计算以及一些鼠标的移动轨迹，实测这 4 个值固定或者随机生成即可，再往下走会遇到给变量去赋值的情况，这里的 V 就是 md5 方法：

这里主要说一下 rp 参数以及 tt 参数是怎么生成的，其他参数可以固定，向上观察，找到明显的+号地方，我们发现 rp 参数是这样定义的：

直接引库复现即可：

const CryptoJS = require("crypto-js");

let gtt = '019924a82c70bb123aae90d483087f94';

let challenge = '7d59427b8c64734df3d8aa8585311fac';

let rp = CryptoJS.MD5(gtt + challenge + 1986).toString();

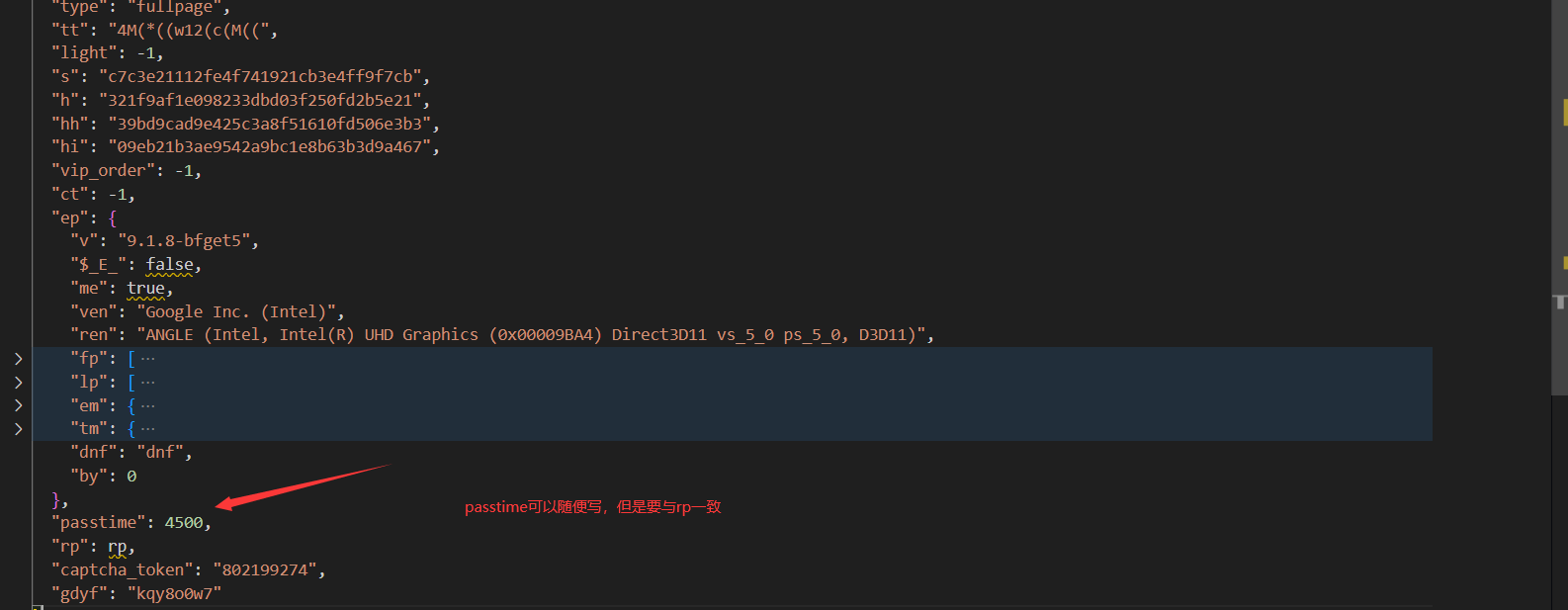
至此，我们的 nr 分析到此结束，第二个 w 复现如下：

nr = {"自行生成"};

# nr 如上，ot 为上一个 w 的 key，保持一致！

w2 = R['$_HDZ'](c['encrypt'](fe['stringify'](nr), Ot));

第三个 w

最后一个 w 大伙都很熟悉了，没有研究过的可以阅读下这篇文章【验证码逆向专栏】某验三代滑块验证码逆向分析，讲解的更为详细，本文简单分析一下。

走到这里，我们已经成功百分之 80 了，我们依旧从栈的入口进入，搜索关键参数"\u0077" ，果然，峰回路转，又回到了这里：

明显，这个和我们第一个 w 生成的方式是一模一样的：

u = r[$_CAHJS(737)]()

l = V[$_CAHJS(392)](gt[$_CAIAK(254)](o), r[$_CAIAK(744)]())

h = m[$_CAIAK(792)](l)

w = h + u

可以直接按第一个 w 的方法直接引库，或者直接扣下整个模块即可。

这里，我们打印 o 参数，看看 o 参数中哪些是固定不变的，哪些是动态变化的：

userresponse：滑动距离 + challenge 的值；
passtime：滑块滑动时间；
imgload：图片加载时间；
aa：轨迹加密；
h9s9：每天 key、value 会变，固定即可；
rp：gt + 32 位 challenge + passtime，再经过 MD5 加密。

发现这里有我们上面扣过的 rp，我们直接用上面的代码复现即可，不懂观察的，无脑去扣，只会影响我们拔刀的速度：

var CryptoJS = require("crypto-js");

gt = '019924a82c70bb123aae90d483087f94'

challenge = '7d59427b8c64734df3d8aa8585311fac'

var rp = CryptoJS.MD5(gtt + challenge + 476).toString()

再往上，我们就可以看到 userresponse 与 aa 参数定义的部分：

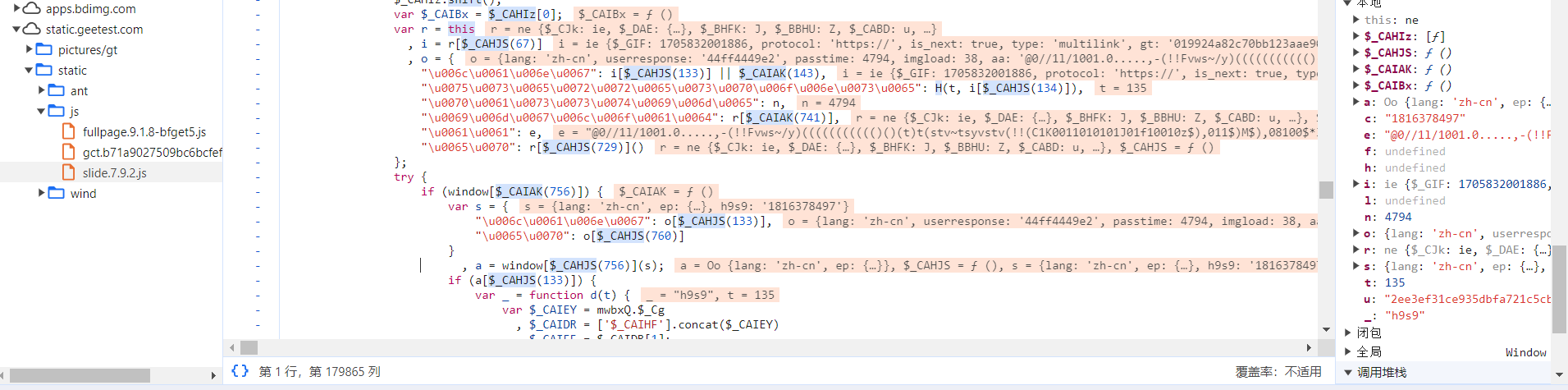
// t 为滑动距离，i[$_CAHJS(134)] 为最新的 challenge

var userresponse = H(t, i[$_CAHJS(134)])

进入 H 函数，将 H 函数扣下来即可：

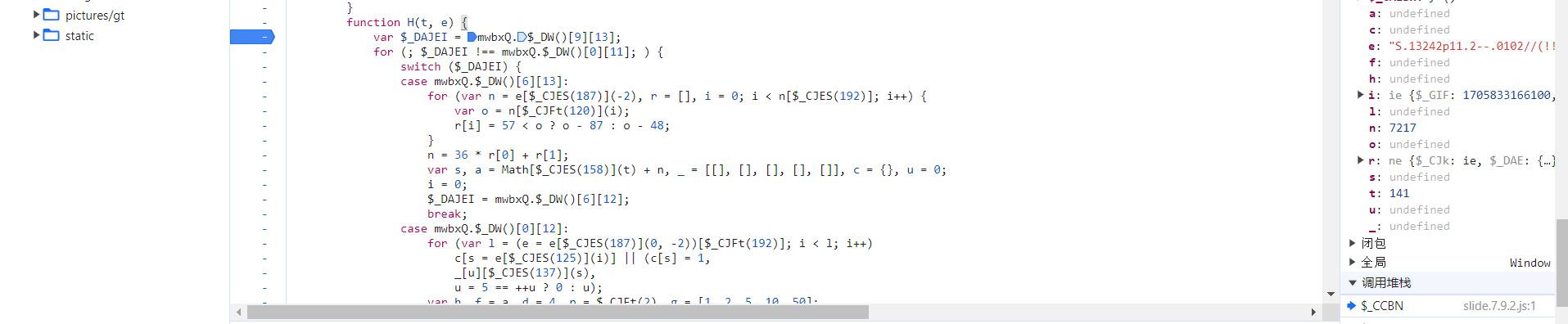
会提示 mwbxQ 不存在，我们把代码放入 nodepad 中，折叠代码：

发现，这个函数在开头就定义，我们把他扣一下即可，即可成功完成 H 的工作，自然这个 userresponse 也就不成问题了。

接下来我们分析 aa，我们看到 aa 参数是由 e 定义的，e 是由上一个函数传过来的，所以我们跟栈，找到 e 定义的地方：

l = n[$_DAAAU(985)][$_CJJJU(1075)](n[$_CJJJU(985)][$_CJJJU(1073)](), n[$_CJJJU(67)][$_CJJJU(1033)], n[$_DAAAU(67)][$_CJJJU(345)]);

$_CJJJU(1075)](n[$_CJJJU(985)][$_CJJJU(1073)]() 为轨迹加密结果，n[$_CJJJU(67)][$_CJJJU(1033)] 为 c 值，n[$_DAAAU(67)][$_CJJJU(345)]) 为 s 值。我们进入 $_CJJJU(1075)](n[$_CJJJU(985)][$_CJJJU(1073)] 中，找到轨迹加密的地方。我们发现 this[$_BEGJO(359)] 为轨迹数组：

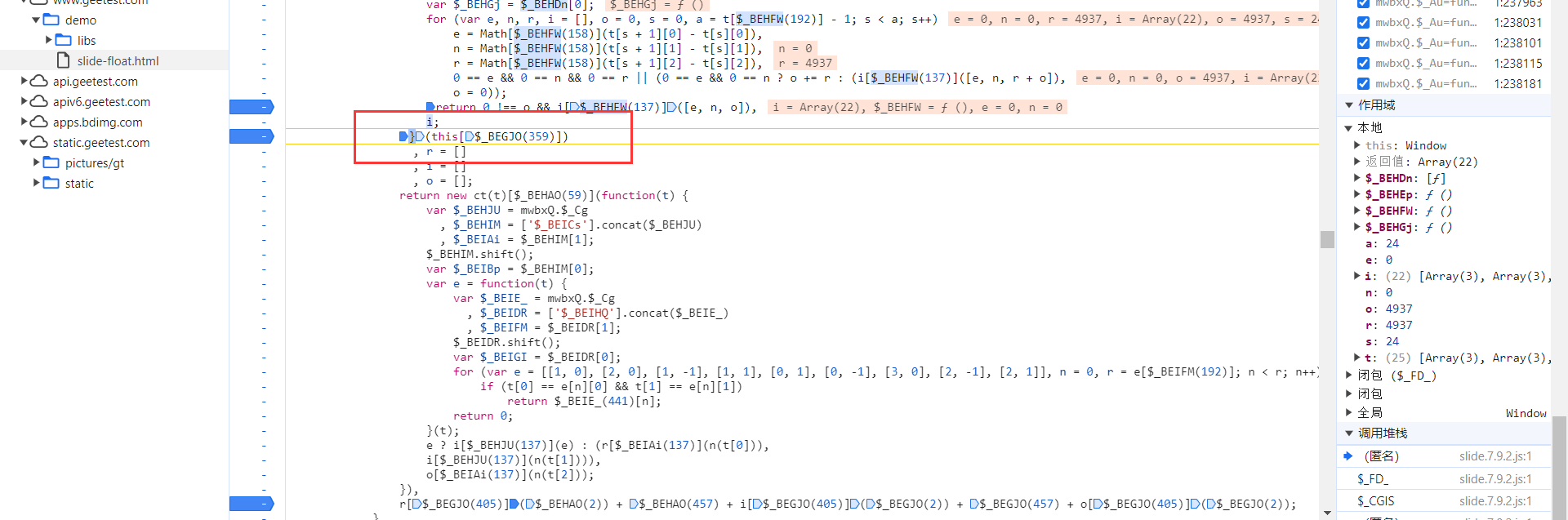
我们将整个函数扣下来，将函数改写，将轨迹当参数传到里面，改写如下，缺什么补什么，最快速的办法，就是利用 nodepad 折叠，可以直观的看到函数分布情况，将可以看到的有用的放进去，然后运行，缺什么补什么即可。附上部分代码：

function ct(t) {

  ........................................................................

  此处省略，具体缺什么取扣什么，补进来就行

W['prototype'] = {

        "\u0024\u005f\u0046\u0044\u004c": function (trace) {

            var $_BEGJp = _tkts.$_Ch

                , $_BEGIy = ['$_BEHCk'].concat($_BEGJp)

                , $_BEHAJ = $_BEGIy[1];

            $_BEGIy.shift();

            var $_BEHBv = $_BEGIy[0];

            function n(t) {

                var $_DBEA_ = _tkts.$_Dm()[0][10];

                for (; $_DBEA_ !== _tkts.$_Dm()[0][9];) {

                    switch ($_DBEA_) {

                        case _tkts.$_Dm()[4][10]:

                            var e = $_BEGJp(454)

                                , n = e[$_BEGJp(159)]

                                , r = $_BEHAJ(82)

                                , i = Math[$_BEHAJ(310)](t)

                                , o = parseInt(i / n);

                            n <= o && (o = n - 1),

                            o && (r = e[$_BEGJp(176)](o));

                            var s = $_BEGJp(82);

                            return t < 0 && (s += $_BEGJp(413)),

                            r && (s += $_BEHAJ(445)),

                            s + r + e[$_BEGJp(176)](i %= n);

                            break;

                    }

                }

            }

    }

aa = W['prototype']['\u0024\u005f\u0042\u0042\u0045\u0049'](W['prototype']['\u0024\u005f\u0046\u0044\u004c'](trace), C, S);

console.log(aa)

```

至此，aa 参数分析完毕，至此第三个 w 参数分析完毕，结束了嘛？并没有~

底图还原

 def restore_picture():

    img_list = ["./乱序缺口背景图.png", "./乱序背景图.png"]

    for index, img in enumerate(img_list):

        image = Image.open(img)

        s = Image.new("RGBA", (260, 160))

        ut = [39, 38, 48, 49, 41, 40, 46, 47, 35, 34, 50, 51, 33, 32, 28, 29, 27, 26, 36, 37, 31, 30, 44, 45, 43, 42,

              12, 13, 23, 22, 14, 15, 21, 20, 8, 9, 25, 24, 6, 7, 3, 2, 0, 1, 11, 10, 4, 5, 19, 18, 16, 17]

        height_half = 80

        for inx in range(52):

            c = ut[inx] % 26 * 12 + 1

            u = height_half if ut[inx] > 25 else 0

            l_ = image.crop(box=(c, u, c + 10, u + 80))

            s.paste(l_, box=(inx % 26 * 10, 80 if inx > 25 else 0))

        if index == 0:

            s.save("./缺口背景图片.png")

        else:

            s.save("./背景图片.png")

restore_picture()

识别缺口

这里分为 A 方案和 B 方案：

A 方案

import io

from PIL import Image

import cv2

import numpy as np

# 将 Image 转换为 Mat，通过 flag 可以控制颜色

def pilImgToCv2(img: Image.Image, flag=cv2.COLOR_RGB2BGR):

    return cv2.cvtColor(np.asarray(img), flag)

# 弹窗查看图片

def showImg(bg: cv2.Mat, name='test', delay=0):

    cv2.imshow(name, bg)

    cv2.waitKey(delay)

    cv2.destroyAllWindows()

def getDistance(img: Image.Image, slice: Image.Image):

    # 通过 pilImgToCv2 将图片置灰

    # 背景图和滑块图都需要做相同处理

    grayImg = pilImgToCv2(img, cv2.COLOR_BGR2GRAY)

    # showImg(grayImg) # 可以通过它来看处理后的图片效果

    graySlice = pilImgToCv2(slice, cv2.COLOR_BGR2GRAY)

    # 做边缘检测进一步降低干扰，阈值可以自行调整

    grayImg = cv2.Canny(grayImg, 255, 255)

    # showImg(grayImg) # 可以通过它来看处理后的图片效果

    graySlice = cv2.Canny(graySlice, 255, 255)

    # 通过模板匹配两张图片，找出缺口的位置

    result = cv2.matchTemplate(grayImg, graySlice, cv2.TM_CCOEFF_NORMED)

    maxLoc = cv2.minMaxLoc(result)[3]

    # 匹配出来的滑动距离

    distance = maxLoc[0]

    # 下面的逻辑是在图片画出一个矩形框来标记匹配到的位置，可以直观的看到匹配结果，去掉也可以的

    sliceHeight, sliceWidth = graySlice.shape[:2]

    # 左上角

    x, y = maxLoc

    # 右下角

    x2, y2 = x + sliceWidth, y + sliceHeight

    resultBg = pilImgToCv2(img, cv2.COLOR_RGB2BGR)

    cv2.rectangle(resultBg, (x, y), (x2, y2), (0, 0, 255), 2)

    # showImg(resultBg)，可以通过它来看处理后的图片效果

    print(distance)

    return distance, resultBg

sliceimgpath = './slice.png'

imgpath = './缺口背景图片.png'

getDistance(Image.open(imgpath), Image.open(sliceimgpath))

B 方案

slide = ddddocr.DdddOcr(det=False, ocr=False)

with open('bg.jpg', 'rb') as f:

    target_bytes = f.read()

with open('fullpage.jpg', 'rb') as f:

    background_bytes = f.read()

img = cv2.imread("bg.jpg")

res = slide.slide_comparison(target_bytes, background_bytes)

print(res)

轨迹模拟

import random

def __ease_out_expo(sep):

    '''

        轨迹相关操作

    '''

    if sep == 1:

        return 1

    else:

        return 1 - pow(2, -10 * sep)

def get_slide_track(distance):

    """

    根据滑动距离生成滑动轨迹

    :param distance: 需要滑动的距离

    :return: 滑动轨迹<type 'list'>: [[x,y,t], ...]

        x: 已滑动的横向距离

        y: 已滑动的纵向距离, 除起点外, 均为0

        t: 滑动过程消耗的时间, 单位: 毫秒

    """

    if not isinstance(distance, int) or distance < 0:

        raise ValueError(f"distance类型必须是大于等于0的整数: distance: {distance}, type: {type(distance)}")

    # 初始化轨迹列表

    slide_track = [

        [random.randint(-50, -10), random.randint(-50, -10), 0],

        [0, 0, 0],

    ]

    # 共记录count次滑块位置信息

    count = 40 + int(distance / 2)

    # 初始化滑动时间

    t = random.randint(50, 100)

    # 记录上一次滑动的距离

    _x = 0

    _y = 0

    for i in range(count):

        # 已滑动的横向距离

        x = round(__ease_out_expo(i / count) * distance)

        # y = round(__ease_out_expo(i / count) * 14)

        # 滑动过程消耗的时间

        t += random.randint(10, 50)

        if x == _x:

            continue

        slide_track.append([x, _y, t])

        _x = x

    slide_track.append(slide_track[-1])

    return slide_track

结果验证