LeetCode46全排列(回溯入门)

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

题目描述

• 难度：中等

• 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案

• 示例 1

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• 示例 2

输入：nums = [0,1]
输出：[[0,1],[1,0]]

• 示例 3

输入：nums = [1]
输出：[[1]]

个人回溯和46题的理解

• 在很多刷题文章和书籍中，此题都被用做回溯算法的第一题，可见该题很有代表性，搞定此题意味着对回溯有了最基本的了解，当然就个人感受而言，以此作为回溯的第一题弊端也不小：本以为掌握了基本套路，刷其他回溯题的时候套上去即可，结果后来发下一道题都套不成功...

• 套不成功？是因为此题没有代表性吗？当然不是，这是道典型的回溯算法题，但个人的感觉是：解题的关键不是套用模板，而是对回溯思想的理解，我个人的理解是：深度至上

• 所谓深度至上，就是弄清楚在当前深度能做什么，例如46题全排列，一个深度意味着可选数字中做了一轮选择，每选中一个，都牢牢占据这一层的固定位置，下面的子树都要有他

• 只要理解了深度至上，就清楚在当前做任何事情的时候都要确保深度固定，下图是[1,2]两个数字全排列的手绘图，边上数字表示选择，方框中的数字表示选择后的结果，请看蓝色框，在选择2的时候，要牢记当深度只能有一个数字，于是，刚才选择1的时候记录存在路径中的1就要果断删除，牢记当前层应该占据哪个位置，回溯的效果就有了

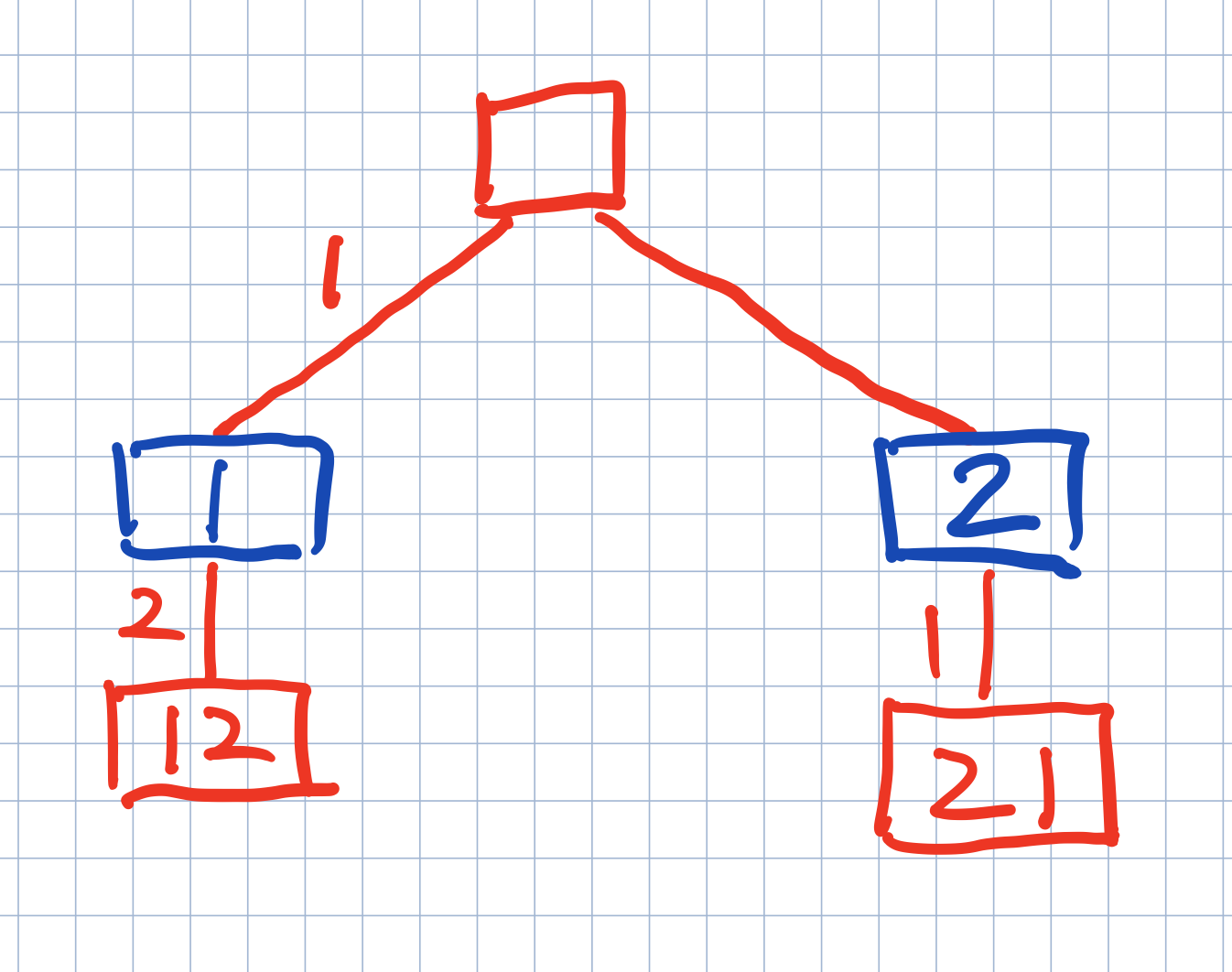
解题思路

• 要用回溯算法解此题，有几个关键要注意

• 全排列，意味着相同数字只要排列不同，也能算作结果的一种

• 虽然不推荐用模板去套，但回溯该有的几个核心概念还是不能少的：

1. 终止条件：只要组合的数字达到给定数字的长度，就可以终止了

2. 路径：就是正在组合的元素，可以用数组表达

• 此外还要有个辅助参数，用于记录那些值不能参与组合，以上图为例，在蓝色那一层如果选择了1，那么在下一层就不能再选择1了，所以在组合的时候，要有地方可以查到1不可用

编码

• 接下来可以写代码了，如下，有几处要注意的地方稍后会提到

public class L0046 {

    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        // 回溯过程中的重要辅助参数：标记nums数组中有哪些已经使用过
        boolean[] used = new boolean[nums.length];
        // 回溯过程中的重要辅助参数：路径
        int[] path = new int[nums.length];

        dfs(nums, used, path, 0);
        return res;
    }

    public void dfs(int[] nums, boolean[] used, int[] path, int depth) {
        // 终止条件(深度达到)
        // 搜集：栈入res
        // 本题的终止条件是一次组合的长度达到数组长度
        if (depth==nums.length) {
            // 搜集结果
            // 千万注意：这个path一直在使用中，所以不能把path放入res中，而是path的元素
//            res.add(Arrays.stream(path).boxed().collect(Collectors.toList()));

            List<Integer> list = new ArrayList<>();
            for(int val : path) {
                list.add(val);
            }

            res.add(list);
            return;
        }

        // for循环
        for (int i=0;i<nums.length;i++) {
            // 如果当前数字没有用到，就标记，进入path，再做dfs
            if (!used[i]) {
                used[i] = true;
                // 注意，path的下标千万不要用i！
                // 例如1和2的全排列，在制造[2,1]的时候，i=1，但此时要修改的是path[i]，
                // 所以path的下标应该是depth
                path[depth] = nums[i];
                // 一次递归，深度要加一
                dfs(nums, used, path, depth+1);
                used[i] = false;
            }
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> list = new L0046().permute(new int[] {1,2,3});

        list.forEach(one -> {
           Tools.printOneLine(one);
        });

    }
}

• 上述代码有以下几处要注意

1. res用于搜集达到终止条件的记录，也就是数字组合结果
2. dfs方法就是本次回溯操作的核心方法
3. 下图红色箭头所指代码就是本题最重要的一行，可见for循环的执行过程中，修改的都是path数组的同一个位置的值，这就是刚才提到的深度至上，只有进入了下面的dfs方法后，深度变化，修改的path数组的位置才会发生变化

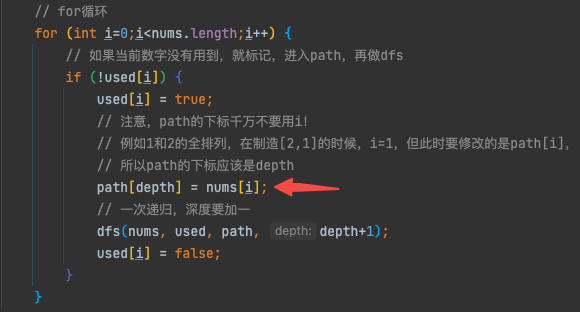
1. used数组用来记录深度调用过程中，那些数字已经被使用了，当前不要再使用
2. 很多回溯的代码中，用栈对象保持path中的数据，入栈push，出栈pop都是标准操作，但是本题中用char数组，再配合depth，就可以满足需要了，这种原始类型的使用也会带来更好的性能

执行结果

• 写完代码提交，执行结果如下，超过100.00%的提交

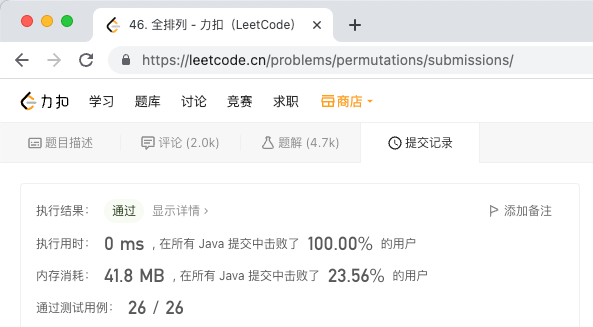
• 至此，回溯入门实战已经完成，此时需要强烈提示：代码中那个for循环，在每一层都遍历nums的所有元素，那是此题的特殊操作，千万不要以为是模板或者套路，其他回溯题中，不会像此题这样每一层都遍历的

欢迎关注博客园：程序员欣宸

学习路上，你不孤单，欣宸原创一路相伴...