UVA 11722 几何概型

第六周A题 - 几何概型

Time Limit:1000MS     Memory Limit:0KB     64bit IO Format:%lld & %llu

 

Description

You are going from Dhaka to Chittagong by train and you came to know one of your old friends is going
from city Chittagong to Sylhet. You also know that both the trains will have a stoppage at junction
Akhaura at almost same time. You wanted to see your friend there. But the system of the country is
not that good. The times of reaching to Akhaura for both trains are not fixed. In fact your train can
reach in any time within the interval [t1, t2] with equal probability. The other one will reach in any
time within the interval [s1, s2] with equal probability. Each of the trains will stop for w minutes after
reaching the junction. You can only see your friend, if in some time both of the trains is present in the
station. Find the probability that you can see your friend.
Input
The first line of input will denote the number of cases T (T < 500). Each of the following T line will
contain 5 integers t1, t2, s1, s2, w (360 ≤ t1 < t2 < 1080, 360 ≤ s1 < s2 < 1080 and 1 ≤ w ≤ 90). All
inputs t1, t2, s1, s2 and w are given in minutes and t1, t2, s1, s2 are minutes since midnight 00:00.
Output
For each test case print one line of output in the format ‘Case #k: p’ Here k is the case number and
p is the probability of seeing your friend. Up to 1e − 6 error in your output will be acceptable.
Sample Input
2
1000 1040 1000 1040 20
720 750 730 760 16
Sample Output
Case #1: 0.75000000
Case #2: 0.67111111

题解：给你两辆火车的到达时间的区间【t1-t2】【s1-s2】，到达后停留时间为w分钟，求坐这两辆火车的人相遇的概率

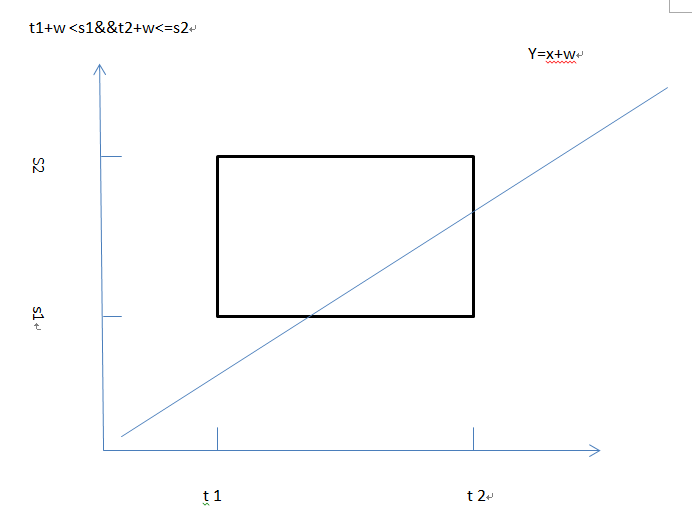
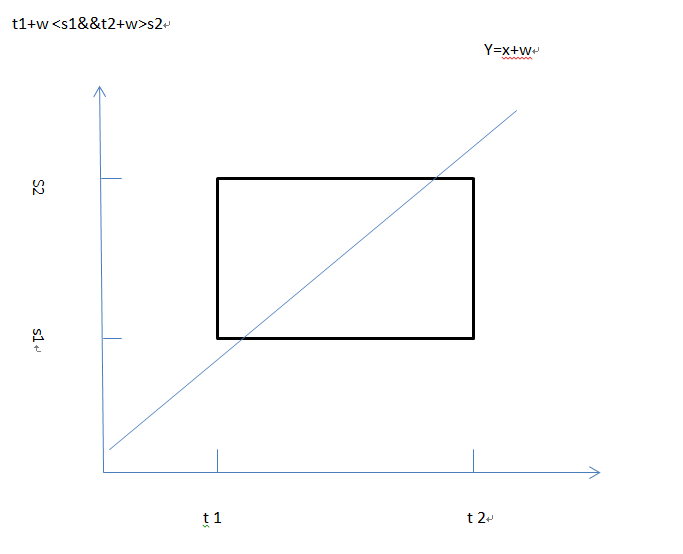
求概率的问题，要用到线性规划，不然很难解决

如果t2+w<s1的话说明无论如何不可能相遇

然后有四种情况,y=x+w,       y=x-w可直接代入-w

#include<iostream>
#include<cstdio>
using namespace std;
double t1,s1,t2,s2,w;
double juge(double ww)
{
    double s=(t2-t1)*(s2-s1);
    if(t2+ww<s1)
        return ;
    if(t1+ww<=s1)
    {
        if(t2+ww<=s2)
            return 0.5*(t2+ww-s1)*(t2+ww-s1);  //
        else
            return 0.5*(t2+ww-s2+t2+ww-s1)*(s2-s1); //
    }
    if(t1+ww<s2)
    {
        if(t2+ww<=s2)
            return 0.5*(t2-t1)*(t2+ww-s1+t1+ww-s1);  //
        else
            return s-0.5*(s2-ww-t1)*(s2-ww-t1);          //
    }
    else return s;
}
int main()
{
    int t,k=;
    cin>>t;
    while(t--)
    {
        cin>>t1>>t2>>s1>>s2>>w;
        double yinying=juge(w)-juge(-w);
        yinying/=(t2-t1)*(s2-s1);
        printf("Case #%d: %.8lf\n",k++,yinying);
    }
}