[AI]神经网络章2 神经网络中反向传播与梯度下降的基本概念

反向传播和梯度下降这两个词，第一眼看上去似懂非懂，不明觉厉。这两个概念是整个神经网络中的重要组成部分，是和误差函数/损失函数的概念分不开的。

神经网络训练的最基本的思想就是：先“蒙”一个结果，我们叫预测结果a，看看这个预测结果和事先标记好的训练集中的真实结果y之间的差距，然后调整策略，再试一次，这一次就不是“蒙”了，而是有依据地向正确的方向靠近。如此反复多次，一直到预测结果和真实结果之间相差无几，亦即|a-y|->0，就结束训练。

在神经网络训练中，我们把“蒙”叫做初始化，可以随机，也可以根据以前的经验给定初始值。即使是“蒙”，也是有技术含量的。

通俗地理解反向传播

举个通俗的例子，Bob拿了一支没有准星的步枪，或者是准星有bug，或者是Bob眼神儿不好看不清靶子，或者是雾很大......反正就是Bob很倒霉。第一次试枪后，拉回靶子一看，弹着点偏左了，于是在第二次试枪时，Bob就会有意识地向右侧偏几毫米，再看靶子上的弹着点，如此反复几次，Bob就会掌握这支步枪的脾气了。下图显示了Bob的5次试枪过程：

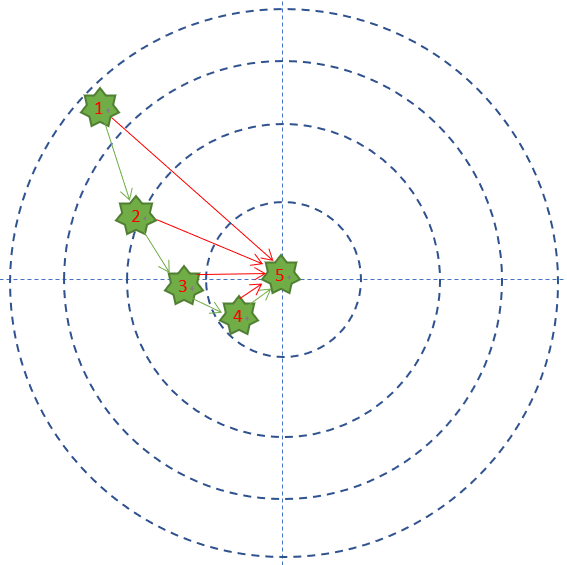
在这个例子中：

• 每次试枪弹着点和靶心之间的差距就叫做误差，可以用一个误差函数来表示，比如差距的绝对值，如图中的红色线。
• 一共试枪5次，就是迭代/训练了5次的过程 。
• 每次试枪后，把靶子拉回来看弹着点，然后调整下一次的射击角度的过程，叫做反向传播。注意，把靶子拉回来看和跑到靶子前面去看有本质的区别，后者容易有生命危险，因为还有别的射击者。一个不恰当的比喻是，在数学概念中，人跑到靶子前面去看，叫做正向微分；把靶子拉回来看，叫做反向微分。
• 每次调整角度的数值和方向，叫做梯度。比如向右侧调整1毫米，或者向左下方调整2毫米。如图中的绿色矢量线。

上图是每次单发点射，所以每次训练样本的个数是1。在实际的神经网络训练中，通常需要多个样本，做批量训练，以避免单个样本本身采样时带来的误差。在本例中，多个样本可以描述为连发射击，假设一次可以连打3发子弹，每次的离散程度都类似，如下图所示：

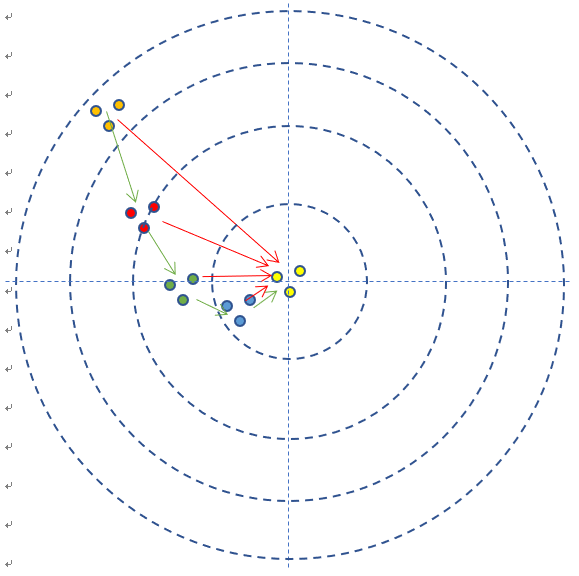
• 如果每次3发子弹连发，这3发子弹的弹着点和靶心之间的差距之和再除以3，叫做损失，可以用损失函数来表示。

其实损失就是所有样本的误差的总和，所以有时候损失函数可以和误差函数混用概念。

其实射击还不这么简单，如果是远距离狙击，还要考虑空气阻力和风速，在神经网络里，空气阻力和风速可以对应到隐藏层的概念上。

用数学概念理解反向传播

我们再用一个纯数学的例子来说明反向传播的概念。

假设我们有一个函数 z=x∗y，其中:x=w∗2+b,y=b+1，即:z=(w∗2+b)∗(b+1)z=x∗y，其中:x=w∗2+b,y=b+1，即:z=(w∗2+b)∗(b+1)

关系如下图：

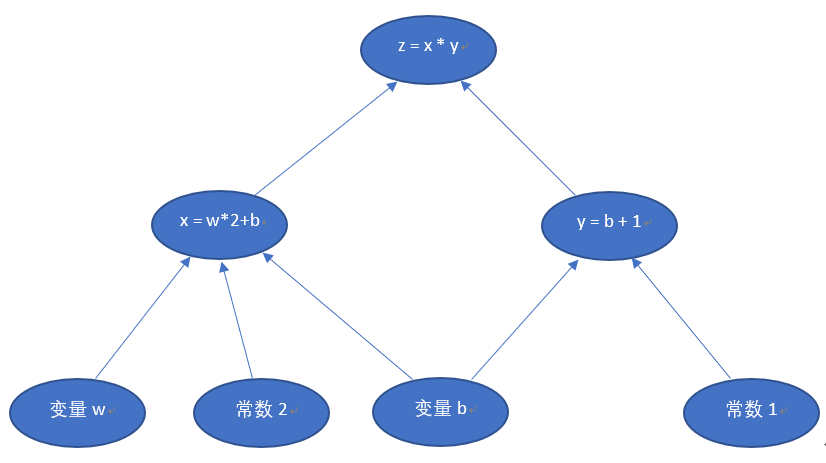
注意这里x, y, z不是变量，w, b是才变量，因为在神经网络中，我们要最终求解的是w和b的值，x,y,z只是样本值。

当w = 3, b = 4时，会得到如下结果

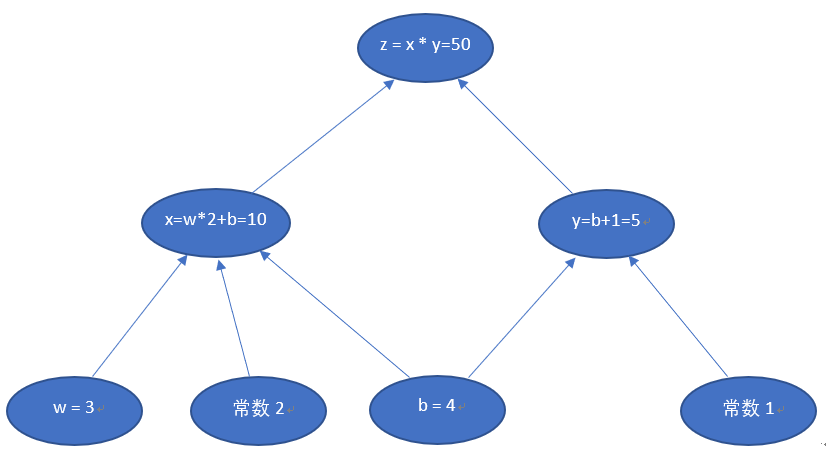
最终的z值，受到了前面很多因素的影响：变量w，变量b，计算式x，计算式y。常数是个定值，不考虑。目前的z=50，如果我们想让z变大一些，w和b应该如何变化呢？

我们从z开始一层一层向回看，图中各节点关于变量b的偏导计算结果如下图：

因为z = x * y，其中x = w * 2 + b，y = b + 1
所以：

∂z∂b=∂z∂x∗∂x∂b+∂z∂y∗∂y∂b=5∗1+10∗1=15

其中：

∂z∂x=∂∂x(x∗y)=y=5

∂z∂y=∂∂y(x∗y)=x=10

∂x∂b=∂∂b(w∗2+b)=1

∂y∂b=∂∂b(b+1)=1

有一个很有趣的问题是：z = x * y = 10 * 5 = 50，表面看起来x=10，y=5，似乎x对z的贡献较大。那么x的微小变化和y的微小变化对z来说，哪一个贡献大呢？

我们假设只有x变化时，△x = 0.1, 则z = (x + △x) * y = 10.1 * 5 = 50.5

我们再假设只有y变化时，△y = 0.1, 则z = x * (y +△y) = 10 * 5.1 = 51

50.5 < 51，说明y的微小变化对z的贡献比较大，这个从

∂z∂x=∂∂x(x∗y)=5<∂z∂y=∂∂y(x∗y)=10

和这两个值的比较来看也可以证明。而△x和△y就可以理解为梯度值。

同理，我们也可以得到图中各变量对w的偏导值：

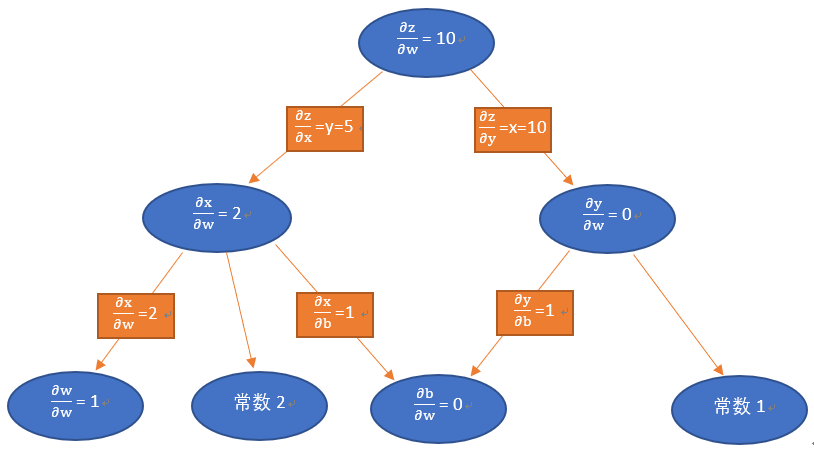
从以上两图可以看出，反向微分保留了所有变量（包括中间变量）对结果z的影响。若z为误差函数，则对图进行一次计算，可以得到所有节点对z的影响，即梯度值，下一步就可以利用这些梯度值来更新w和b的权重。

w的变化和b的变化，哪一个对z的变化贡献大？从图中还可以注意到：

∂z∂b=15

∂z∂w=10

所以每次w和b的变化值是不相同的，b的变化会比w大一些，也就是每一步的跨度大一些，这个是与z = xy = (w2+b)*(b+1)这个算式相关的，并不代表神经网络中实际情况。

反向传播的实际计算过程（单变量）

还是用上面的例子，目前：

• w=3w=3
• b=4b=4
• x=w∗2+b=10x=w∗2+b=10
• y=b+1=5y=b+1=5
• z=x∗y=50z=x∗y=50

假设我们最终的目的想让z = 60，只改变b的值，如何实现？
答案就是偏导数：

∂z∂b=ΔzΔb=15

目前z=50, 距离60相差10，所以我们令Δz=60−50=10Δz=60−50=10，则：

ΔzΔb=15=10ΔbΔzΔb=15=10Δb

所以:

Δb=0.66667Δb=0.66667

再带入式子中（顺便说一句，下面这个计算过程就叫做前向计算）

• w=3
• b=4+0.66667=4.66667
• x=w∗2+b=10.66667
• y=b+1=5.66667
• z=x∗y=10.66667∗5.66667=60.4445

一下子超过60了，咋办？再来一次（下面的过程就叫做反向传播）：

我们令Δz=60−60.4445=−0.4445，则：

ΔzΔb=15=−0.4445Δb

所以:

Δb=−0.02963

再带入式子中：

• w=3
• b=4.66667−0.02963=4.63704
• x=w∗2+b=10.63704
• y=b+1=5.63704
• z=x∗y=10.63704∗5.63704=59.96

咦哈！59.96了！再迭代几次，应该可以近似等于60了，直到误差不大于0.00001时，我们就可以结束迭代了，对于计算机来说，这些运算的执行速度很快。

有的同学会说了：这个问题不是用数学公式倒推求解一个二次方程，就能直接得到准确的b值吗？是的！但是我们是要说明机器学习的方法，机器并不会解二次方程，而且很多时候不是用二次方程就能解决实际问题的。而上例所示，是用机器所擅长的迭代计算的方法来不断逼近真实解，这就是机器学习的真谛！而且这种方法是普遍适用的。

用二维平面函数说明梯度下降原理

很多资料中会用下面这个图来说明梯度下降，但是都没有说清楚以下几个问题：

1） 为啥用这个看上去像y=x2y=x2族的函数来说明梯度下降？
2） 在最低点的左侧，梯度值是负数；在最低点的右侧，梯度值是正数。为什么说是“下降”？
3） 为什么1—>2，2—>3等等的连线不是这条曲线的切线呢，而好像是弦线？

为何用y=x2y=x2函数？

这是因为有一种损失函数的形式就是均方差，亦即：

loss=∑i(ai−yi)2

其中a是本次迭代的预测结果，y是样本中的真实结果。我们的目的就是在这个函数上求最小值，使loss最小，这样样本值和预测值就会非常非常接近，以便于我们以后预测不在样本中的真实数据。

为什么说是“梯度下降”？

“梯度下降”，刚接触这个词时，我总是往“降低难度”或“降低维度”方面去理解，因为有个“下降”的动词在里面。而实际上，“下降”在这里面的含义是“与导数相反的方向”的意思。

我们假设上面这个图形的函数是y=(x−1)2+0.001y=(x−1)2+0.001，则y′x=2(x−1)yx′=2(x−1)。

• 在点B上，这个函数的切线（绿色）是指向下方的（Y轴方向），所以是个负数：假设XBXB = 0.1, 则y′=2∗(0.1−1)=−1.8y′=2∗(0.1−1)=−1.8。
• 在F点上，切线（绿色）向上：假设XFXF = 1.5, 则y′=2∗(1.5−1)=1y′=2∗(1.5−1)=1，是个正数。

而在标准的权重更新公式里：

w=w–η∗Δw

b=b–η∗Δb

可以看到无论是w还是b，都是用上一次的权重值减去步长××梯度。注意，我们在上一个例子中，是用b直接加减ΔbΔb的，并没有用到η，或者说η=1。这样的问题就是步长可能过大，一下子就跳过了极值点。

• 当梯度(y')是正数时，即点F的位置，x=x−η∗1x=x−η∗1，切线向上，x值会变小，权重值会从右侧向x=1靠近；
• 当梯度(y')是负数时，亦即点B的位置，切线向下，x值会变大：x=x−η∗(−1.8)=x+η∗1.8x=x−η∗(−1.8)=x+η∗1.8，最终运算结果变成了加法，与切线方向相反，权重值会从左侧向x=1靠近。

所以总体上看，无论x在极值的左侧还是右侧，都会向中间（坡底）靠拢，确实是“下降”了。

不知不觉中，我们已经接触到了第一个神经网络中的超参η，即步长值，这个值对于神经网络训练非常重要，决定了训练时间的长短，它的取值一般是从0.1到0.0001，自己选择。

曲线和弦线的关系？

1. 我们先知道了A点的切线的方向，亦即黄色的线，但是不知道长度
2. 我们有步长值η，以及梯度下降公式X1=X0–η∗dxX1=X0–η∗dx
3. 因为y′x的导数dx=2(X−1),η=0.1,X0=0.2,于是有X1=X0–0.1∗2(X0−1)=0.36yx′的导数dx=2(X−1),η=0.1,X0=0.2,于是有X1=X0–0.1∗2(X0−1)=0.36，这就等同于我们知道了切线的长度，亦即绿色的线的长度和方向都确定了
4. 然后我们可以画出红色的线（亦即弦线）

所以，弦线在这里面没啥用途，只是表示一个迭代跳跃的动作而已。实际的变化值已经由绿色的线定义好了。