BZOJ1047或洛谷2216 [HAOI2007]理想的正方形

BZOJ原题链接

洛谷原题链接

显然可以用数据结构或\(ST\)表或单调队列来维护最值。

这里采用单调队列来维护。

先用单调队列维护每一行的最大值和最小值，区间长为正方形长度。

再用单调队列维护之前维护出的每行最值数组的每一列的最大值和最小值，区间同上。

最后维护出的数组其实就是以每个点为左上角的正方形中的最值，直接扫一遍求最小的差即可。

借用洛谷题解里大佬的图以更好说明：



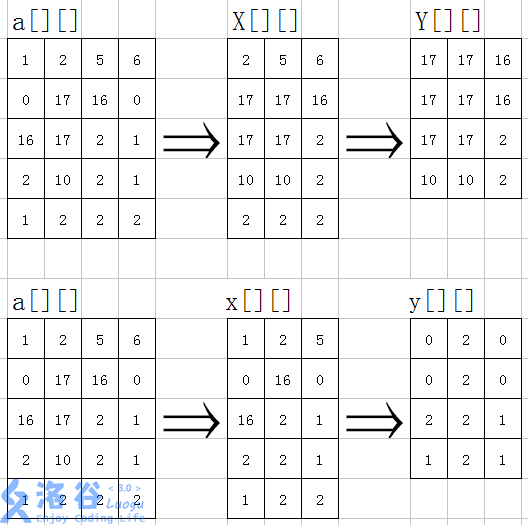
(\(X,x\)分别是维护出原矩阵中行的最大、最小值，\(Y,y\)分别是维护\(X,x\)中列的最大、最小值)

#include<cstdio>
using namespace std;
const int N = 1010;
const int M = 2e6 + 10;
int a[N][N], ma_x[N][N], mi_x[N][N], ma_y[N][N], mi_y[N][N], qma[M], qmi[M];
inline int re()
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c == '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
inline int minn(int x, int y)
{
	return x < y ? x : y;
}
int main()
{
	int i, j, n, m, k, lmi, lma, rmi, rma, o, oo, mi = 1e9;
	n = re();
	m = re();
	k = re();
	for (i = 1; i <= n; i++)
		for (j = 1; j <= m; j++)
			a[i][j] = re();
	for (i = 1; i <= n; i++)
	{
		lmi = lma = 1;
		rmi = rma = 0;
		for (j = 1; j < k; j++)
		{
			for (; lma <= rma && a[i][qma[rma]] <= a[i][j]; rma--);
			for (; lmi <= rmi && a[i][qmi[rmi]] >= a[i][j]; rmi--);
			qma[++rma] = j;
			qmi[++rmi] = j;
		}
		for (; j <= m; j++)
		{
			for (; lma <= rma && j - qma[lma] + 1 > k; lma++);
			for (; lmi <= rmi && j - qmi[lmi] + 1 > k; lmi++);
			for (; lma <= rma && a[i][qma[rma]] <= a[i][j]; rma--);
			for (; lmi <= rmi && a[i][qmi[rmi]] >= a[i][j]; rmi--);
			qma[++rma] = j;
			qmi[++rmi] = j;
			ma_x[i][j - k + 1] = a[i][qma[lma]];
			mi_x[i][j - k + 1] = a[i][qmi[lmi]];
		}
	}
	for (i = 1, o = m - k + 1; i <= o; i++)
	{
		lmi = lma = 1;
		rmi = rma = 0;
		for (j = 1; j < k; j++)
		{
			for (; lma <= rma && ma_x[qma[rma]][i] <= ma_x[j][i]; rma--);
			for (; lmi <= rmi && mi_x[qmi[rmi]][i] >= mi_x[j][i]; rmi--);
			qma[++rma] = j;
			qmi[++rmi] = j;
		}
		for (; j <= n; j++)
		{
			for (; lma <= rma && j - qma[lma] + 1 > k; lma++);
			for (; lmi <= rmi && j - qmi[lmi] + 1 > k; lmi++);
			for (; lma <= rma && ma_x[qma[rma]][i] <= ma_x[j][i]; rma--);
			for (; lmi <= rmi && mi_x[qmi[rmi]][i] >= mi_x[j][i]; rmi--);
			qma[++rma] = j;
			qmi[++rmi] = j;
			ma_y[j - k + 1][i] = ma_x[qma[lma]][i];
			mi_y[j - k + 1][i] = mi_x[qmi[lmi]][i];
		}
	}
	for (i = 1, o = n - k + 1, oo = m - k + 1; i <= o; i++)
		for (j = 1; j <= oo; j++)
			mi = minn(mi, ma_y[i][j] - mi_y[i][j]);
	printf("%d", mi);
	return 0;
}