膨胀卷积与IDCNN

Dilation 卷积，也被称为：空洞卷积、膨胀卷积。

一、一般的卷积操作：

首先，可以通过动态图，理解正常卷积的过程：

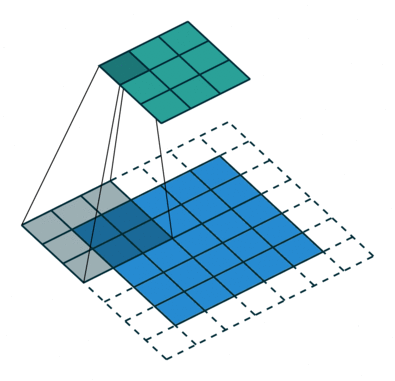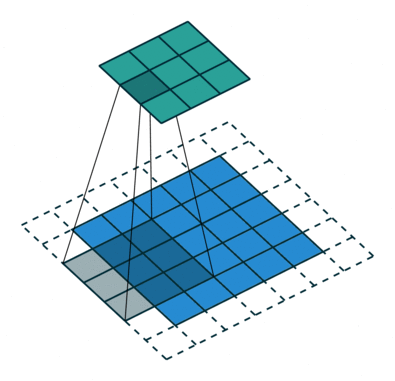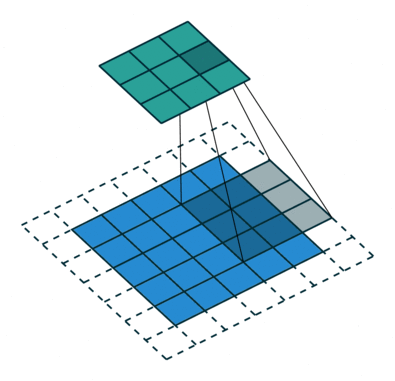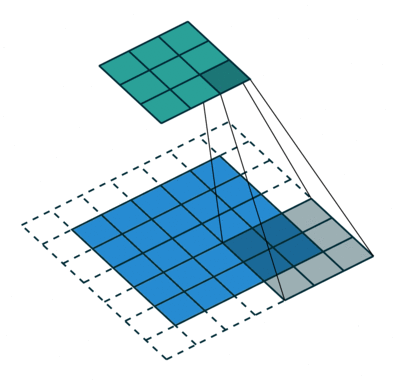
如上图，可以看到卷积操作。

对于CNN结构，通常包括如下部分：

输入层 （input layer）---  卷积计算层 （CONV）--- 激励层（RELU） --- 池化层（Pooling） --- 全连接层（FC）

通常利用卷积来实现数据的特征提取。卷积层还有一个权值共享的原则：用一句话表达就是每个神经元只关注一个特征。

当然卷积完经过激励层做一个非线性映射，输出后就到Pooling layer了。

池化层的作用：

(1)压缩数据和参数的量，减小过拟合。

(2)增大感受野。

主要两种方法：Max Pooling  和  Average Pooling

对于有些算法，池化完还需要upsampling获得原始数的尺寸进行后续操作。由于这种通过卷积操作存在内部数据丢失的问题，存在信息损失，有人提出了dilated conv算法，即不通过池化获得较大的视野，并减小信息损失。

二、膨胀卷积

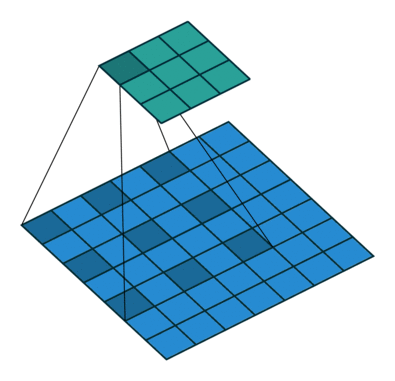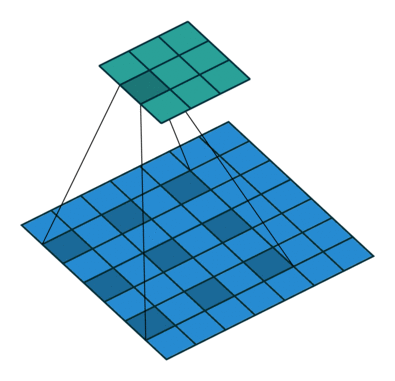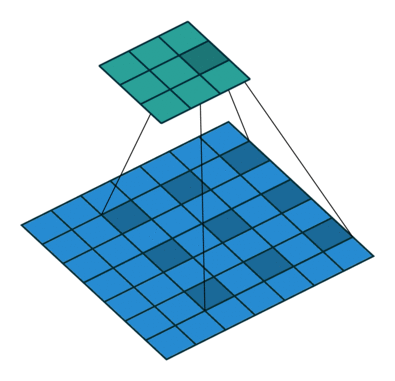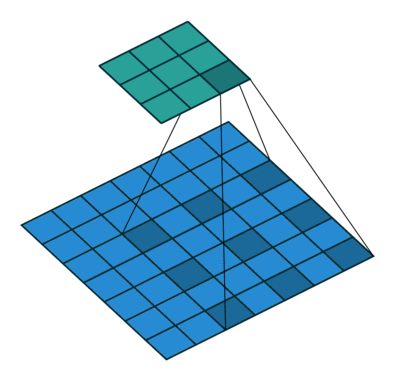
如上图，膨胀卷积的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者自然语言处理中需要较长的sequence信息依赖的问题中，都能很好的应用。

在tensorflow中代码为：

tf.nn.atrous_conv2d(value,filters,rate,padding,name=None）

　　value：输入的卷积图像，[batch, height, width, channels]。

　 filters：卷积核，[filter_height, filter_width, channels, out_channels]，通常NLP相关height设为1。

　　rate：正常的卷积通常会有stride，即卷积核滑动的步长，而膨胀卷积通过定义卷积和当中穿插的rate-1个0的个数，实现对原始数据采样间隔变大。

　　padding：”SAME”：补零   ； ”VALID”：丢弃多余的

 三、IDCNN(Iterated Dilated CNN)

模型是4个大的相同结构的Dilated CNN block拼在一起，每个block里面是dilation width为1, 1, 2的三层Dilated卷积层，所以叫做 Iterated Dilated CNN。参考代码实现：

layers = [
            {
                'dilation': 1
            },
            {
                'dilation': 1
            },
            {
                'dilation': 2
            },
        ]
finalOutFromLayers = []
totalWidthForLastDim = 0
for j in range(4):
    for i in range(len(layers)):
        dilation =layers[i]['dilation']
        isLast = True if i == (len(layers) - 1) else False
        w = tf.get_variable("filterW",shape=[1, filter_width, num_filter,num_filter],initializer=tf.contrib.layers.xavier_initializer())
        b = tf.get_variable("filterB", shape=[num_filter])
        conv = tf.nn.atrous_conv2d(layerInput,w,rate=dilation,padding="SAME")
        conv = tf.nn.bias_add(conv, b)
        conv = tf.nn.relu(conv)
        if isLast:
            finalOutFromLayers.append(conv)
            totalWidthForLastDim += num_filter
        layerInput = conv
finalOut = tf.concat(axis=3, values=finalOutFromLayers)

　　通过代码可以看到具体的IDCNN的实现流程以及输出的结合方式。