OpenCascade BRep Format Description

OpenCascade BRep Format Description

eryar@163.com

摘要Abstract：本文结合OpenCascade的BRep格式描述文档和源程序，对BRep格式进行分析，详细说明BRep的数据组织形式。结合源程序，可以对OpenCascade中Modeling Data模块中的模型数据结构进行理解。

关键字Key Words：OpenCascade, BRep Format, ModelingData

一、引言 Introduction

OpenCascade中的BRep格式主要用来存储3D模型，也可用来存储由下列元素组成的模型：vertices, edges, wires, faces, shells, solids, compsolids, compounds, edge triangulations, face triangulations, polylines on triangulations, space location and orientation.

本格式的目的就是为了便于理解，也使用了类似BNF的定义方式。以下章节都是按下面的格式组织的：

l 该部分的示例；

l 该部分的类BNF定义；

l 该部分的详细说明；

l 该部分的源程序片段。

二、通用结构 Format Common Structure

BRep格式文件的读写采用了ASCII的编码方式，该格式的数据都是文本形式存储。

BRep格式使用了下面的BNF术语：

1) <\n>：换行；

2) <_\n>：

3) <_>：空格；

4) <flag>：标志位：0和1；

5) <int>：整数，范围-231到231-1；

6) <real>：实数，范围-1.7976931348623159X10308到1.7976931348623158X10308；

7) <2D point>：二维点，两个实数；

8) <3D point>：三维点，三个实数；

9) <2D direction>：二维方向矢量，两个实数，平方和为1，即为单位方向矢量；

10) <3D direction>：三维方向矢量，三个实数，平方和为1，即为单位方向矢量；

11) <+>

BRep格式包含以下部分：

1) <content type>

2) <version>

3) <locations>

4) <geometry>

5) <shapes>

<content type>部分：

<content type>也可以有其它的值。

<version>部分：

不同版本之间的区别将会在本文档中说明。

三、<locations>部分 Section <locations>

示例：

BNF 定义：

详细说明：

<location data 1>定义了3X4的矩阵Q，描述了三维空间的线性变换，并满足如下约定：

矩阵Q是线性变换矩阵，它可以通过矩阵乘法将一个点（x, y, z）变换成另外一点（u, v, w）：

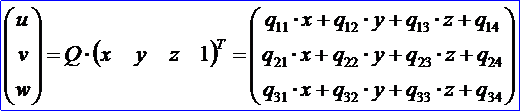
Q也可能是以下基本变换矩阵的组合：

1) 平移变换矩阵：

2) 绕任意轴旋转的变换矩阵，轴的方向为D（Dx, Dy, Dz），旋转角度ψ：

3) 缩放变换矩阵：

4) 中心对称变换矩阵：

5) 轴对称变换矩阵：

6) 平面对称变换矩阵：

<location data 2>解释为组合变换的幂。<location data 2>是整数对li, pi的序列。这个序列将被解释为：

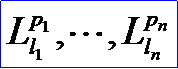
Lli是<location record>部分的变换矩阵。

读取<locations>部分的类为TopTools_LocationSet，程序代码如下所示：

  //=======================================================================
  //function : Read
  //purpose  :
  //=======================================================================
  void  TopTools_LocationSet::Read(Standard_IStream& IS)
  {
    myMap.Clear();

    char buffer[];
   Standard_Integer l1,p;

   IS >> buffer;
   if (strcmp(buffer,"Locations")) {
     cout << "Not a location table "<<endl;
     return;
   }

   Standard_Integer i, nbLoc;
   IS >> nbLoc;

   TopLoc_Location L;
   gp_Trsf T;

   //OCC19559
   Message_ProgressSentry PS(GetProgress(), "Locations", , nbLoc, );
   for (i = ; i <= nbLoc&& PS.More(); i++, PS.Next()) {
     if ( !GetProgress().IsNull() )
       GetProgress()->Show();

     Standard_Integer typLoc;
     IS >> typLoc;

     if (typLoc == ) {
       ReadTrsf(T,IS);
       L = T;
     }

     else if (typLoc == ) {
       L = TopLoc_Location();
       IS >> l1;
       while (l1 != ) {
     IS >> p;
     TopLoc_Location L1 = myMap(l1);
     L = L1.Powered(p) *L;
     IS >> l1;
       }
     }

     if (!L.IsIdentity()) myMap.Add(L);
   }
 }

虽然代码风格不好，缩进、括号什么的都不工整，看起来很吃力，但是结合源程序，对上面的详细说明的理解还是很有帮助的。

其中变量nbLoc是<location record count>的值，成员变量myMap是TopLoc_Location的一个map。当是<location record 1>时把<location data 1>都放到TopLoc_Location的map中。当是<location record 2>时将li的变换矩阵TopLoc_Location乘pi次方。<flag>0表示<location data 2>的结束。

四、<geometry>部分

<geometry>包含以下子部分：

1．<2D curves>

2．<3D curves>

3．<3D polygons>

4．<polygons on triangulations>

5．<surfaces>

6．<triangulations>

读取<geometry>部分的类为BRepTools_ShapeSet，程序代码如下所示：

  //=======================================================================
  //function : ReadGeometry
  //purpose  :
  //=======================================================================
  void  BRepTools_ShapeSet::ReadGeometry(Standard_IStream& IS)
  {
    //OCC19559
    myCurves2d.SetProgress(GetProgress());
    myCurves.SetProgress(GetProgress());
   mySurfaces.SetProgress(GetProgress());

   if ( !GetProgress().IsNull()) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->NewScope ( , "2D Curves" );
   }
   myCurves2d.Read(IS);

   if ( !GetProgress().IsNull()) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();

     GetProgress()->NewScope ( , "3D Curves" );
   }
   myCurves.Read(IS);

   if ( !GetProgress().IsNull()) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();

     GetProgress()->NewScope ( , "3D Polygons" );
   }
   ReadPolygon3D(IS);
   if ( !GetProgress().IsNull() ) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();

     GetProgress()->NewScope ( , "Polygons On Triangulation" );
   }
   ReadPolygonOnTriangulation(IS);
   if ( !GetProgress().IsNull()) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();

     GetProgress()->NewScope ( , "Surfaces" );
   }
   mySurfaces.Read(IS);
   if ( !GetProgress().IsNull() ) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();

     GetProgress()->NewScope ( , "Triangulations" );
   }
   ReadTriangulation(IS);
   if ( !GetProgress().IsNull()) {
     if( GetProgress()->UserBreak() ) return;
     GetProgress()->EndScope();
     GetProgress()->Show();
   }
 }

4.1 子部分<3D curves>

示例：

BNF定义：

详细说明：

由Curves开始，后面是曲线的数量，再下面是每条曲线的具体数据。

读取<curves>部分的类为GeomTools_CurveSet，程序代码如下所示：

  #define LINE      1
   #define CIRCLE    2
   #define ELLIPSE   3
   #define PARABOLA  4
   #define HYPERBOLA 5
   #define BEZIER    6
   #define BSPLINE   7
   #define TRIMMED   8
   #define OFFSET    9
  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  Standard_IStream& GeomTools_CurveSet::ReadCurve(Standard_IStream& IS,
                          Handle(Geom_Curve)& C)
  {
    Standard_Integer ctype;

    try {
      OCC_CATCH_SIGNALS
      IS >> ctype;
      switch (ctype) {

      case LINE :
        {
          Handle(Geom_Line) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case CIRCLE :
        {
          Handle(Geom_Circle) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case ELLIPSE :
        {
          Handle(Geom_Ellipse) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case PARABOLA :
        {
          Handle(Geom_Parabola) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case HYPERBOLA :
        {
          Handle(Geom_Hyperbola) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case BEZIER :
        {
          Handle(Geom_BezierCurve) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case BSPLINE :
        {
          Handle(Geom_BSplineCurve) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case TRIMMED :
        {
          Handle(Geom_TrimmedCurve) CC;
          IS >> CC;
          C = CC;
        }
        break;

      case OFFSET :
        {
          Handle(Geom_OffsetCurve) CC;
          IS >> CC;
          C = CC;
        }
        break;

      default:
        {
          Handle(Geom_Curve) CC;
          GeomTools::GetUndefinedTypeHandler()->ReadCurve(ctype,IS,CC);
         C = CC;
       }
     }
   }
   catch(Standard_Failure) {
 #ifdef DEB
     Handle(Standard_Failure) anExc = Standard_Failure::Caught();
     cout <<"EXCEPTION in GeomTools_CurveSet::ReadCurve(..)!!!" << endl;
     cout << anExc << endl;
 #endif
     C = NULL;
   }
   return IS;
 }

因为重载了操作符>>，使不同的类调用了不同的处理函数。

因为读取点和方向用得很频繁，所以将读取点和方向的函数程序先列出如下所示：

 //=======================================================================
  //function : ReadPnt
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS, gp_Pnt& P)
  {
    Standard_Real X=.,Y=.,Z=.;
    IS >> X >> Y >> Z;
    P.SetCoord(X,Y,Z);
   return IS;
 }

 //=======================================================================
 //function : ReadDir
 //purpose  :
 //=======================================================================
 static Standard_IStream& operator>>(Standard_IStream& IS, gp_Dir& D)
 {
   Standard_Real X=.,Y=.,Z=.;
   IS >> X >> Y >> Z;
   D.SetCoord(X,Y,Z);
   return IS;
 }

4.1.1 <3D curve record 1>-Line

示例：

BNF定义：

详细说明：

<3D curve record 1>定义了直线。直线数据由一个三维点P和一个三维方向矢量D组成。通过点P且方向为D的直线由下面的参数方程来定义：

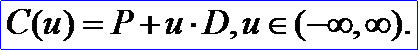
示例数据表示的直线为通过点P（1，0，3），方向D（0，1，0），得到的参数方程为：

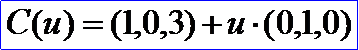
读取直线部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_Line)& L)
  {
    gp_Pnt P(.,.,.);
    gp_Dir AX(.,.,.);
   IS >> P >> AX;
   L = new Geom_Line(P,AX);
   return IS;
 }

4.1.2 <3D curve record 2>-Circle

示例：

BNF定义：

详细说明：

<3D curve record 2>定义了圆。圆的数据包含一个三维点P，一个正交坐标系的三个轴的方向N，Dx，Dy，还有一个非负的实数r。其中点P为圆心坐标，圆位于平面的法向量为N的平面上，圆的半径为r。圆的参数方程如下所示：

示例数据表示的圆为：圆心P（1，2，3），位于平面的法向量N（0，0，1），圆的方向Dx＝（1，0，－0），Dy＝（－0，1，0），半径r＝4，其参数方向为：

读取圆部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_Circle)& C)
  {
    gp_Pnt P(.,.,.);
    gp_Dir A(.,.,.),AX(.,.,.),AY(.,.,.);
   Standard_Real R=.;
   IS >> P >> A >> AX >> AY >> R;
   C = new Geom_Circle(gp_Ax2(P,A,AX),R);
   return IS;
 }

4.1.3 <3D curve record 3>-Ellipse

示例：

BNF定义：

详细说明：

<3D curve record 3>定义了椭圆。椭圆的数据包含三维点P，三维正交坐标系N、Dmaj、Dmin和两个非负实数rmaj和rmin，且rmin<=rmaj。椭圆位于中心点P，法向量为N的平面上，且长轴、短轴的方向分别为Dmaj, Dmin，长轴、短轴上的半径分别为rmaj, rmin。椭圆的参数方程定义如下所示：

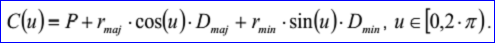
示例数据表示的椭圆的中心点P＝（1，2，3），平面的法向量N＝（0，0，1），长轴方向Dmaj＝（1，0，－0），短轴方向Dmin＝（－0，1，0），长轴半径为5，短轴半径为4，

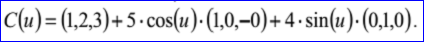
读取椭圆部分的程序代码如下所示：

 //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_Ellipse)& E)
  {
    gp_Pnt P(.,.,.);
    gp_Dir A(.,.,.),AX(.,.,.),AY(.,.,.);
   Standard_Real R1=.,R2=.;
   IS >> P >> A >> AX >> AY >> R1 >> R2;
   E = new Geom_Ellipse(gp_Ax2(P,A,AX),R1,R2);
   return IS;
 }

4.1.4 <3D curve record 4>-Parabola

示例：

BNF定义：

详细说明：

<3D curve record 4>定义了抛物线。抛物线数据包含三维点P，三维正交坐标系坐标轴方向N，Dx，Dy和一个非负的实数f。抛物线通过点P，且位于法向量为N的平面上，焦点长度为f，其参数方程如下所示：

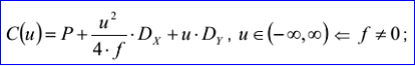
示例数据表示的抛物线过点P＝（1，2，3），位于平面的法向N＝（0，0，1），抛物线的另两个轴方向Dx＝（1，0，－0），Dy＝（－0，1，0），焦点长度f＝16。参数方程为：

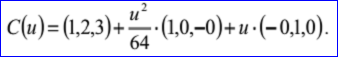
读取抛物线部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_Parabola)& C)
  {
    gp_Pnt P(.,.,.);
    gp_Dir A(.,.,.),AX(.,.,.),AY(.,.,.);
   Standard_Real R1=.;
   IS >> P >> A >> AX >> AY >> R1;
   C = new Geom_Parabola(gp_Ax2(P,A,AX),R1);
   return IS;
 }

4.1.5 <3D curve record 5>-Hyperbola

示例：

BNF定义：

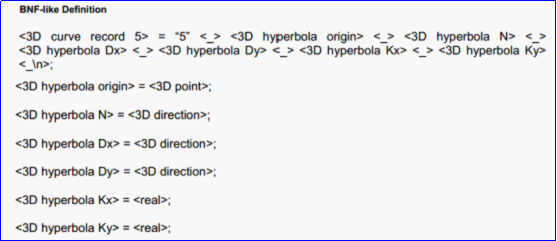
详细说明：

<3D curve record 5>定义了双曲线。双曲线定义数据有三维点P，三维正交坐标系坐标轴方向为N，Dx，Dy和两个非负实数Kx，Ky。双曲线过P点且法向量为N的平面上，其参数方程如下所示：

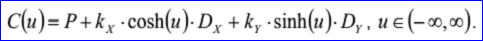
示例数据表示的双曲线过点P＝（1，2，3）且位于的平面的法向N＝（0，0，1），其它的数据Dx＝（1，0，－0），Dy＝（－0，1，0），Kx＝5和Ky＝4。其参数方程为：

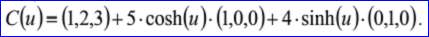
读取双曲线部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_Hyperbola)& H)
  {
    gp_Pnt P(.,.,.);
    gp_Dir A(.,.,.),AX(.,.,.),AY(.,.,.);
   Standard_Real R1=.,R2=.;
   IS >> P >> A >> AX >> AY >> R1 >> R2;
   H = new Geom_Hyperbola(gp_Ax2(P,A,AX),R1,R2);
   return IS;
 }

4.1.6 <3D curve record 6>-Bezier Curve

示例：

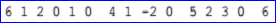
BNF定义：

详细说明：

<3D curve record 6>定义了Bezier曲线。Bezier曲线数据包含有理标志r，曲线的次数m（degree m <= 25查看源代码可知OpenCascade可处理的B样条次数不超过25）和带权的控制点（weight poles）。当有理标志位r＝0时，weight poles就是m+1个三维点：B0，B1...Bn；当有理标志位r＝1时，weight poles就是带权的控制点B0 h0... Bm hm。Bi是三维点，hi是[0，m]正实数，即权因子。当有理标志位r＝0时，即不是有理Bezier曲线时，hi＝1。Bezier曲线参数方程如下所示：

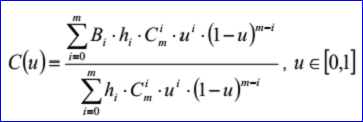
示例数据表示的Bezier曲线是有理Bezier曲线，因其有理标志位r＝1，次数m＝2，带权控制点及权因子分别为：B0＝（0，1，0），h0=4，B1＝（1，－2，0），h1＝5，B2＝（2，3，0），h2＝6。Bezier曲线的参数方程如下所示：

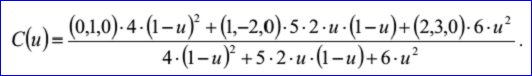
读取Bezier曲线部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_BezierCurve)& B)
  {
    Standard_Boolean rational=Standard_False;
    IS >> rational;

   // poles and weights
   Standard_Integer i=,degree=;
   IS >> degree;

   TColgp_Array1OfPnt poles(,degree+);
   TColStd_Array1OfReal weights(,degree+);

   for (i = ; i <= degree+; i++) {
     IS >> poles(i);
     if (rational)
       IS >> weights(i);
   }

   if (rational)
     B = new Geom_BezierCurve(poles,weights);
   else
     B = new Geom_BezierCurve(poles);

   return IS;
 }

4.1.7 <3D curve record 7>-B-Spline curve

示例：

BNF定义：

详细说明：

<3D curve record 7>定义了B-Spline曲线。B-Spline曲线包含了有理标志位r，曲线次数m<=25，控制点数n>=2，重节点数k，带权控制点wieght poles和重节点multiplicity knots。

当有理标志位r＝0时，是非有理B样条曲线，weight poles有n个三维点B1，...，Bn；当有理标志位r＝1时，是有理B样条曲线，weight poles是n个带权控制点对：B1, h1, .... Bn, hn。这里Bi表示一个三维点，hi表示一个[0，1]正实数。当有理标志位r＝0时，hi＝1。

重节点有k对u1, q1, ... uk, qk。这里ui是重复度为qi>=1的节点。

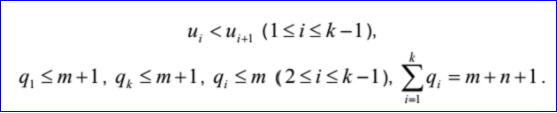
B-Spline曲线的参数方程如下所示：

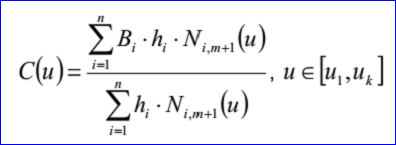
其中Ni,j有如下的递归定义：

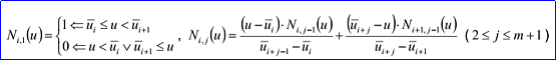
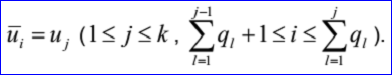
示例数据表示的B样条曲线为：有理标志位r＝1，次数m＝1，控制点数n＝3，重节点数k＝5，带权控制点：B1＝（0，1，0），h1＝4，B2＝（1，－2，0），h2＝5，B3＝（2，3，0），h3＝6；重节点u1＝0，q1＝1，u2＝0.25，q2＝1，u3＝0.5，q3＝1，u4＝0.75，q4＝1，u5＝1，q5＝1。B-Spline曲线的参数方程如下所示：

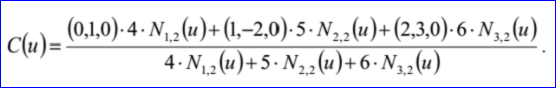
读取B-Spline曲线部分的程序代码如下所示：

  //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_BSplineCurve)& B)
  {

    Standard_Boolean rational=Standard_False,periodic=Standard_False;
   IS >> rational >> periodic;

   // poles and weights
   Standard_Integer i=,degree=,nbpoles=,nbknots=;
   IS >> degree >> nbpoles >> nbknots;

   TColgp_Array1OfPnt poles(,nbpoles);
   TColStd_Array1OfReal weights(,nbpoles);

   for (i = ; i <= nbpoles; i++) {
     IS >> poles(i);
     if (rational)
       IS >> weights(i);
   }

   TColStd_Array1OfReal knots(,nbknots);
   TColStd_Array1OfInteger mults(,nbknots);

   for (i = ; i <= nbknots; i++) {
     IS >> knots(i) >> mults(i);
   }

   if (rational)
     B = new Geom_BSplineCurve(poles,weights,knots,mults,degree,periodic);
   else
     B = new Geom_BSplineCurve(poles,knots,mults,degree,periodic);

   return IS;
 }

4.1.8 <3D curve record 8>-Trimmed Curve

示例：

BNF定义：

详细说明：

<3D curve record 8>定义了裁剪曲线（trimmed curve）。裁剪曲线数据包含：两个实数umin，umax和<3D curve record>，且umin<umax。裁剪曲线是将<3D curve record>描述的曲线B限制在[umin，umax]。裁剪曲线的参数方程如下所示：

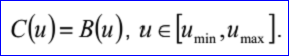
示例数据表示的裁剪曲线为：umin＝－4，umax＝5，曲线B(u)＝（1，2，3）+u（1，0，0）。裁剪曲线的参数方程如下所示：

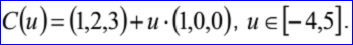
读取裁剪曲线部分的程序代码如下所示：

 //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================

  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_TrimmedCurve)& C)
  {
    Standard_Real p1=.,p2=.;
   IS >> p1 >> p2;
   Handle(Geom_Curve) BC;
   GeomTools_CurveSet::ReadCurve(IS,BC);
   C = new Geom_TrimmedCurve(BC,p1,p2);
   return IS;
 }

4.1.9 <3D curve record 9>-Offset Curve

示例：

BNF定义：

详细说明：

<3D curve record 9>定义了偏移曲线（offset curve）。偏移曲线的数据包含偏移距离d，偏移方向D和曲线数据<3D curve record>。偏移曲线是将<3D curve record>描述的曲线沿矢量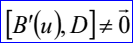偏移距离d后的结果。偏移曲线的参数方程如下所示：

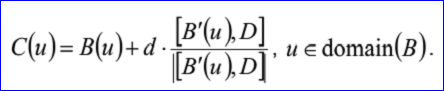
示例数据表示的偏移曲线为偏移距离d＝2，方向D＝（0，1，0），基曲线B(u)＝（1，2，3）+u（1，0，0），其参数方程如下所示：

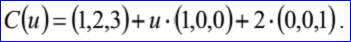
读取偏移曲线部分程序代码如下所示：

 //=======================================================================
  //function : ReadCurve
  //purpose  :
  //=======================================================================
  static Standard_IStream& operator>>(Standard_IStream& IS,
                      Handle(Geom_OffsetCurve)& C)
  {
    Standard_Real p=.;
    IS >> p;
   gp_Dir D(.,.,.);
   IS >> D;
   Handle(Geom_Curve) BC;
   GeomTools_CurveSet::ReadCurve(IS,BC);
   C = new Geom_OffsetCurve(BC,p,D);
   return IS;
 }

未完，待续……