单纯形方法（Simplex Method）

最近在上最优理论这门课，刚开始是线性规划部分，主要的方法就是单纯形方法，学完之后做了一下大M算法和分段法的仿真，拿出来与大家分享一下。单纯形方法是求解线性规划问题的一种基本方法。

线性规划就是在一系列不等式约束下求目标函数最大值或最小值的问题，要把数学中的线性规划问题用计算机来解决，首先要确定一个标准形式。

将所给的线性规划问题化为标准形式：

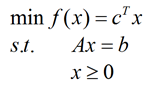
s.t.是英文subject to 的简写，意思是受约束，也就是说第一个方程受到后面两个方程的约束。对于求最大值问题可以将目标函数加负号转换为最小值问题。

对于求最大值问题可以将目标函数加负号转换为最小值问题。

其他的问题就是将实际问题中的不等式约束改为等式约束，主要方法是引进松弛变量和剩余变量，以及将自有变量转换为非负变量。

①对于不等式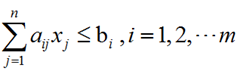，引入松弛变量将其变为等式形式如下：

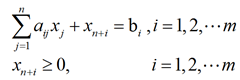
②对于不等式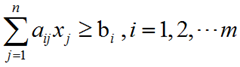，引入剩余变量将其变为等式形式如下：

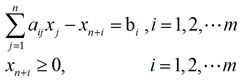
③若变量为自有变量（可取正、负或零，符号无限制），则引入两个非负变量将其表示如下：

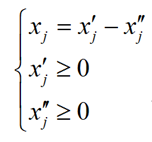
关于线性规划问题的解：

确定了标准形式，我们就针对这个标准形式讨论一下线性规划问题的解。线性规划问题的解能满足标准形式中约束条件的向量X的值，但只有最优解才能使目标函数值最小。

对于上文中的标准形式，约束矩阵A是一个m*n维矩阵，且m<n，所以一定可以从A中找到一个满秩m*m矩阵。这个矩阵就称作矩阵A的一个基阵，矩阵A就可以写作 [B N] , 相应的解 x 也可以写成 x=(xB,xN)’，那么 Ax=b 就变为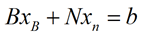，左式两端同乘B矩阵的逆，得到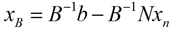。由此引出下列名词：

基阵：非奇异矩阵（满秩矩阵、可逆矩阵）B

基向量：基阵B由m个线性无关的向量组成，称之为基向量

基变量：向量xB各分量，与基向量对应的xB中的m个分量成为基变量

非基变量：向量xN各分量

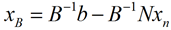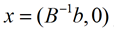基本解：令xN各分量为0，由得到的解称为基阵B对应的基本解

基本可行解：当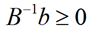成立时，称基本解为基本可行解，因为只有满足所有分量不小于0，才符合标准形式中的约束条件（最后一条）。

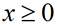单纯形表

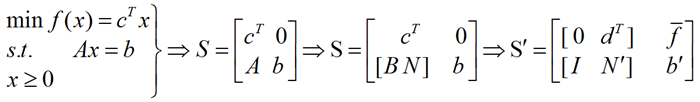
如上图所示，在做单纯形表时，我们要找到这么一个满秩矩阵B，而且要通过行变换把它化为单位阵，同时把这个单位阵上方对应的向量c中元素变为0。也就是说，在标准的单纯形表中，在表的第一行中，基变量对应的元素全为0，非基变量对应的元素称之为检验数。这时便找到了此问题的一个基本可行解，此时单纯形表最右边一列的各数从上到下为此基本解对应的目标函数值f和基本解的基变量的值b’（非基变量为0）。

举个例子：

S	X1(非基变量)	X2(非基变量)	X3	X4	X5
f	5（检验数）	10（检验数）	0	0	0	0（目标函数值）
X3	1/14	1/7	1	0	0	1（基变量X3值）
X4	1/7	1/12	0	1	0	1（基变量X4值）
X5	1	1	0	0	1	8（基变量X5值）

这是一个已经变换好的单纯形表，红色部分是b’，也就是此时基本可行解中基变量分别为X3,X4,X5，他们的值分别为1,1,8，对应的基本可行解就是（0,0,1,1,8）。可以看出，此时目标函数值为0。

单纯形方法基本步骤：

初始的单纯形表已经给出了线性规划问题的一个基本可行解，接下来要做的就是判断这个解是否是最优解，如果是的话不用继续找啦，如果不是的话就找一个比这个解更好的解，再进行判断，直到找到最优解。但有的问题是没有最优解的，所以还要判定问题是否无解。

1） 将所给的线性规划问题化为标准形式。

2）找出一个初始的基阵B，作出单纯形表，作为程序的输入（A,C,f,b’）。

3）测试所有的检验数，记录检验数中的正数，若全部小于等于0，则已经找到最优解，计算终止。否则转至4）。

4）测试所有为正的检验数，若在单纯性表中，其所在的列中其他元素全部小于等于0，则此问题无最优解，计算终止，否则转至5）。

5）找出检验数中的最大值，此最大值元素所在列为A(i,:)，令约束条件中约束向量b与A(i,:)的比值为向量r，向量r中为正的最小值为h，计算过程如下图。

S单纯形表	X1	X2	X3	X4	X5
f	5	10（最大值）	0	0	0	0
X3	1/14	1/7	1	0	0	1
X4	1/7	1/12	0	1	0	1
X5	1	1	0	0	1	8

表格中黄色部分组成的向量点除（对应元素相除）红色部分，得到向量（7,12,8），那么7就是我们要找的那个元素，此时记录元素大小h和坐标(i,j)，注意是在S表中行号和列号，此处是2和2（如果有多个相等的最小值则任取一个即可）。

这个元素1/7就是所谓的转轴元（或称基本元），找到他之后要围绕他进行一系列的行变换，称之为换基。步骤如下：

①使转轴元变为1，方法很简单，就是让本行所有元素同时除以转轴元1/7。

②把转轴元所在列的其他元素都变为0，做法是通过一个循环，遍历每一个行（自身所在行除外），每行中与转轴元同列的元素为a，令每行减去转轴元所在行的第a倍即可。转至3）。

理论部分到此为止，如有疏漏欢迎留言（参考书目为黄平的《最优化理论》）

matlab仿真程序编写:

Simplex.m

 

%Simplex Method
function [x,y]=Simplex(f,A,b)
%输入f是检验数的数组，1*n维
%输入A是约束矩阵， m*n维
%输入b是约束向量， 1*m维
%输出x是解向量
%输出y是最优解
%判断输入维数是否相符
%做初始单纯形表
format rat %将结果以分数表示
S=[f 0;A b'];
[n,m]=size(S);
%判断检验数 r<=0
r=find(f>0);
len=length(r);
%有大于0的检验数则进入循环
while(len)
    %检查非负检验数所对列向量元素是否都小于等于0
    for k=1:length(r)
        d=find(S(:,r(k))>0);
        if(length(d)+1==2)
        error('无最优解！！！')
        %break;
        end
    end
    %找到检验数中最大值
    [Rk,j]=max(S(1,1:m-1));
    %b与最大值所在列的比值
    rb=S(2:n,m)./S(2:n,j);
    %把比值中的负数都变无穷
    for p=1:length(rb)
        if(rb(p)<0)
            rb(p)=Inf;
        end
    end
    [h,i]=min(rb);%列向量比值最小值
    % i+1为转轴元行号(在S中)，j为转轴元列号
    i=i+1;
    %进行换基,转轴元置1
    S(i,:)=S(i,:)./S(i,j);
    %转轴元所在列其他元素都置0
    for k=1:n
        if(k~=i)
            S(k,:)=S(k,:)-S(i,:)*S(k,j);
        end
    end
    %判断检验数 r<=0
    r=find(S(1,1:m-1)>0);
    len=length(r);
end
    %检验数全部非正，找到最优解
    %非基变量置0
    x=zeros(1,m-1);
    for i=1:m-1
        %找到基变量
        j=find(S(:,i)==1);%每列中1的个数
        k=find(S(:,i)==0);%每列中0的个数
        if((length(j)+1==2)&&(length(k)+1==n))
            %i为基本元列号，j是行号
            x(i)=S(j,m);
        end
    end
    y=S(1,m);%最优解
    S
end

下面附带一个测试程序(test.m)：

clear all
clc
f=[4 3 0 0 0];
A=[1 1 1 0 0;
   1 2 0 1 0;
   3 2 0 0 1];
b=[50 80 140];
[x,y]=Simplex(f,A,b)
f=[1 1 0 0];
A=[-2 1 1 0;
   1 -1 0 1];
b=[4 2];
[x,y]=Simplex(f,A,b)

仿真结果如下：