Linear Algebra lecture7 note
Computing the nullspace (Ax=0)
Pivot variables-free variables
Special solutions: rref( A)=R

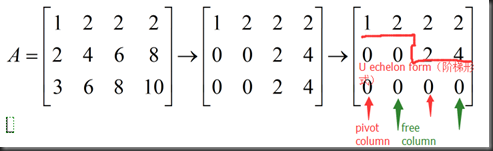
rank of A=the number of pivots=2
由上述矩阵行变换回代可得方程
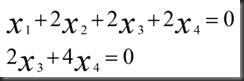
我们自行给free variable对应的x赋值
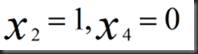
得到一个特解x为
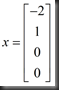 表示的意思是
表示的意思是
再赋一组值
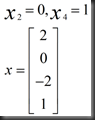 表示的意思是
表示的意思是
以上特解可以组成通解
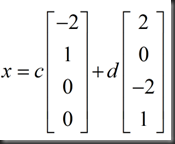
Reduce row(echelon form:zeros above and below pivots) 行最简形

rref (A) means (reduced row echelon form of A)
There are some information that this kind of form tells:
1.pivot rows are row1 and row2
2.pivot cols are col1 and col3
3.this matrix conclude an I(Identity) in it , made by pivot rows and pivot cols
4.全0行表示原行是其他行的线性组合
5.可得知自由列
6.回代得到特解
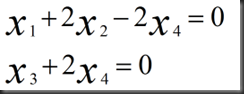
即我们由AX=0到UX=0,最终得到RX=0
交换R中各列,可得如下形式

rref form:
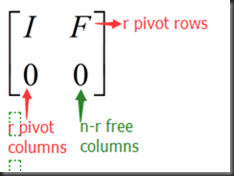
假设N是RX=0的一个特解

回代:
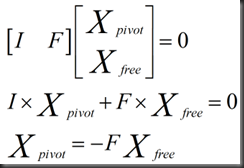
若Xfree赋值单位矩阵I,那么Xpivot可得到-F
特解与F有关,方程得以解出
example:
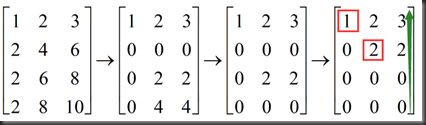
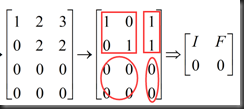
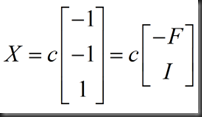
Linear Algebra lecture7 note的更多相关文章
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- Linear Algebra lecture9 note
Linear independence Spanning a space Basis and dimension 以上概念都是针对a bunch of vectors, 不是矩阵里的概念 Supp ...
- Linear Algebra lecture10 note
Four fundamental subspaces( for matrix A) if A is m by n matrix: Column space C(A) in Rm (列空间在m维实 ...
- Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn) rank r r=m solutions exist r=n solutions unique example: 若想方程有解 ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture4 note
Inverse of AB,A^(A的转置) Product of elimination matrices A=LU (no row exchanges) Inverse of AB,A^(A ...
- Linear Algebra lecture3 note
Matrix multiplication(4 ways!) Inverse of A Gauss-Jordan / find inverse of A Matrix multiplication ...
- Codeforces Gym101502 B.Linear Algebra Test-STL(map)
B. Linear Algebra Test time limit per test 3.0 s memory limit per test 256 MB input standard input ...
随机推荐
- 【转】Linux Top 命令解析 比较详细
TOP命令是Linux下常用的性能分析工具,能够实时显示系统中各个进程的资源占用状况. TOP是一个动态显示过程,即可以通过用户按键来不断刷新当前状态.如果在前台执行该命令,它将独占前台,直到用户 ...
- char* 和char[]的区别
以下内容均来自互联网,系笔者汇总并总结. 1. 问题介绍 问题引入:在实习过程中发现了一个以前一直默认的错误,同样char *c = "abc"和char c[]="ab ...
- jQuery---中的动画
show():$('p').show(); show(1000) 里面加参数会让元素在显示的时候动起来 hide():$('p').hide(); hide(1000) 里面加参数让元素在隐藏的时候动 ...
- wp8开发笔记之应用程序真机发布调试
写在前面的话: 相信很多和我一样关注wp8动态以及已经开发了一些wp8应用程序的朋友们都遇到过这样的问题,写的程序在模拟器上进行调试总是显的没什么说服力,想拿真机进行实际测试, 该怎么办才好呢? 进行 ...
- 《C++primer》v5 第8章 IO库 读书笔记 习题答案
8.1.8.2 这一章不咋会啊.. istream &read(istream &is) { int a; auto old_state=is.rdstate(); is.clear( ...
- android4.4以上,快捷实现标题栏透明
方法很简单写一个values-v19的文件夹,当安卓版本大于4.4时便会调用该文件夹下的styles.xml文件 结构如图: styles.xml <resources> <!-- ...
- 关于阿里 阿里巴巴共享业务事业部UED团队 出品的sui基于zepto的开源UI框架的使用心得
1.项目官网地址:http://m.sui.taobao.org/ 2.项目使用可以参考开始使用和示例 3.项目是放在 Github 上的 https://github.com/sdc-alibaba ...
- 用Unity代码通过Xml配置生成GameObject之——前两天掉的坑
1. Resources.Load(path),path不是绝对路径,而是相对"Resources/"的相对路径!如: 要想Instantiate则代码应该如下: string m ...
- Cosh.3
查壳.没有 拖 OD 查找字符串 找到有用的东西 顺线往上看 找到 大概算入口处 下断 就从这里开始 单步下去吧 name的变幻 Serial的变幻 直接翻译出来了 继续看看 ...
- wamp出现You don’t have permission to access/on this server提示的解决方法
本地搭建wamp 输入http://127.0.0.1访问正常,当输入http://localhost/ apache出现You don't have permission to access/on ...
