[您有新的未分配科技点][BZOJ3545&BZOJ3551]克鲁斯卡尔重构树

这次我们来搞一个很新奇的知识点：克鲁斯卡尔重构树。它也是一种图，是克鲁斯卡尔算法求最小生成树的升级版首先看下面一个问题：BZOJ3545 Peaks。

在Bytemountains有N座山峰，每座山峰有他的高度h_i。有些山峰之间有双向道路相连，共M条路径，每条路径有一个困难值，这个值越大表示越难走。

现在有Q组询问，每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰，如果无解输出-1。N<=1e5,M,Q<=5*1e5

上面这个题没有要求在线，因此我们可以离线构造最小生成树，然后当小于等于一个询问的困难值的所有边都加入后，就可以查询当前的询问点。

这种操作只需要主席树上树+启发式合并就可以解决了。（参考资料：主席树上树http://www.cnblogs.com/LadyLex/p/7275164.html，启发式合并http://www.cnblogs.com/LadyLex/p/7275793.html）

但是如果强制在线呢？BZOJ3551 Peaks加强版，在上一题基础上强制在线。

可以用来解决一系列“查询从某个点出发经过边权不超过val的边所能到达的节点”的问题，可以和其他数据结构（比如主席树）套用来维护更加复杂的询问。

克鲁斯卡尔重构树的核心思想是，当添加最小生成树中的边的时候，不在两个点间直接加边，而是新建节点，让边的两个端点所在的联通块的代表点分别作为它的左右儿子节点，然后这个新建的点，就成为这整个连通块的代表点，点权为连边的值（最开始n个叶子节点点权为0）。比如看下面这张图：首先连接（1,2），新建一个点5。再连接（3,4），新建一个点6。然后连接（1,3），连接它们各自联通块的代表点（5,6），再新建一个点7。

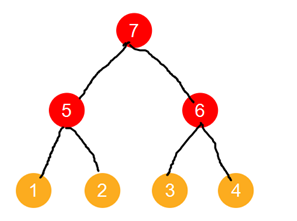
这样得到的树有一个很优雅的性质：一个点的所有子树节点的权值都小于等于它的权值，并且从它开始逐渐向子节点移动，权值是单调不上升的。这个性质是显然的，因为我们在构造树的时候是从小到大插入的边，因此父亲节点的权值一定大于等于子节点的值。

查询时，首先可以在树上倍增得到当前查询点所能够到达的最远的祖先点，那么从这个点能够到达的符合边权限制条件的连通块中的节点，就是祖先点的子树中所有的叶节点。

然后我们按dfs序维护一个主席树上树就可以解决了。

代码见下：

 #include <cstring>
 #include <cstdio>
 #include <algorithm>
 #include <ctime>
 using namespace std;
 const int N=;
 int h[N*],val[N*],n,tot,num,cnt,stack[N],e,adj[N*];
 int f[N*][],bin[],fa[N*],l[N*],r[N*];
 struct edge{int qi,zhong,val;}intn[N*];
 struct link{int zhong,next;}s[N*];
 inline void mission1(int rt){for(int i=;bin[i]<=n;i++)f[rt][i]=f[f[rt][i-]][i-];}
 inline void add(int qi,int zhong){s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;}
 inline bool mt(const edge &a,const edge &b){return a.val<b.val;}
 int find(int a){return (fa[a]==a)?a:fa[a]=find(fa[a]);}
 struct node
 {
     int cnt;node *ch[];
     node(){cnt=;ch[]=ch[]=NULL;}
     inline void update(){cnt=ch[]->cnt+ch[]->cnt;}
 }*null=new node(),*root[*N];
 inline node* newnode(){node *o=new node();o->ch[]=o->ch[]=null;return o;}
 void insert(node *&o,node *old,int l,int r,int pos)
 {
     o->cnt=old->cnt+;
     if(l==r)return;
     int mi=(l+r)>>;
     if(pos<=mi)o->ch[]=old->ch[],o->ch[]=newnode(),insert(o->ch[],old->ch[],l,mi,pos);
     else o->ch[]=old->ch[],o->ch[]=newnode(),insert(o->ch[],old->ch[],mi+,r,pos);
     o->update();
 }
 inline int query(int a,int x,int k)
 {
     int le=,ri=tot;
     for(int j=;~j;j--)
  　　　　if(f[a][j]&&val[f[a][j]]<=x)a=f[a][j];
     node *a1=root[r[a]],*a2=root[l[a]-];
     if(a1->cnt-a2->cnt<k)return -;
     while(le<ri)
     {
         int tmp=a1->ch[]->cnt-a2->ch[]->cnt,mi=(le+ri)>>;
         if(tmp>=k)a1=a1->ch[],a2=a2->ch[],le=mi+;
         else a1=a1->ch[],a2=a2->ch[],k-=tmp,ri=mi;
     }
     return stack[ri];
 }
 void dfs(int rt)
 {
     mission1(rt);l[rt]=++num;
     if(rt<=n)insert(root[num],root[num-],,tot,h[rt]);
     else root[num]=root[num-];
     for(int i=adj[rt];i;i=s[i].next)dfs(s[i].zhong);
     r[rt]=num;
 }
 int main()
 {
     int m,q,ans=,v,x,k;scanf("%d%d%d",&n,&m,&q);
     bin[]=;for(int i=;i<=;i++)bin[i]=bin[i-]<<;
     null->ch[]=null->ch[]=null;
     for(int i=;i<=n*;i++)fa[i]=i;
     for(int i=;i<=n;i++)scanf("%d",&h[i]),stack[i]=h[i];
     for(int i=;i<=m;i++)scanf("%d%d%d",&intn[i].qi,&intn[i].zhong,&intn[i].val);
     sort(stack+,stack+n+);
     tot=unique(stack+,stack+n+)-stack-;
     for(int i=;i<=n;i++)h[i]=lower_bound(stack+,stack+tot+,h[i])-stack;
     sort(intn+,intn+m+,mt);cnt=n;
     for(int i=;i<=m;i++)
     {
         int u=find(intn[i].qi),v=find(intn[i].zhong);
         if(u!=v)
         {
             val[++cnt]=intn[i].val,fa[u]=fa[v]=cnt;
             add(cnt,u),add(cnt,v),f[u][]=f[v][]=cnt;
             if(cnt-n==n-)break;
         }
     }
     for(int i=;i<=cnt;i++)root[i]=newnode();
     for(int i=;i<=cnt;i++)if(!l[i])dfs(find(i));
     while(q--)
     {
         scanf("%d%d%d",&v,&x,&k);
         if(ans!=-)v^=ans,x^=ans,k^=ans;/*去掉这句强制在线可以ACbzoj3545*/
         printf("%d\n",ans=query(v,x,k));
     }
 }

克鲁斯卡尔重构树是个比较小众的知识点，但在处理对口的操作时十分强大。下次你再看到类似询问的时候，不妨想一想克鲁斯卡尔重构树，也许就会柳暗花明又一村:)