Loj 6036 「雅礼集训 2017 Day4」编码 - 2-sat

题目传送门

　　唯一的传送门

题目大意

　　给定$n$个串，每个串只包含 '','','?' ，其中 '?' 至多在每个串中出现1次，它可以被替换为 '' 或 '' 。问是否可能任意两个不同的串不满足一个是另一个的前缀。

　　2-sat的是显然的。

　　枚举每个通配符填0还是1，然后插入Trie树。

　　对于Trie的每个点在2-sat中建点。

　　如果其中一个点被选择，那么它祖先和所有后继的结束点都不能选。（然后逆否命题连边）

　　对于一个包含通配符的串，通配符替换为0以及通配符替换为1的否命题等价，同样，通配符替换为1以及通配符替换为0的否命题等价（连双向边）。

　　对于一个不包含通配符的串，直接它到的节点的从否命题节点连一条到它的有向边。

　　于是我们得到边数平方的优秀做法。

　　考虑前缀和优化，新建一个虚点表示Trie树上，它的祖先的命题都是假。但是这样还有点问题，还要建一个点表示Trie上，它的所有后继的命题都是假。

　　建图比较繁杂，见下图：

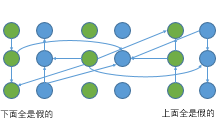
　　然后再说一下处理多个串在Trie树上共点。

　　于是便有了点数$12n$的优秀做法。再由于代码常数巨大无比，成功Loj最慢榜榜首，sad。。。（一定要去学习一下榜首同学点数$4n$的优质做法）

Code

 /**
  * loj.ac
  * Problem#6036
  * Accepted
  * Time: 4346ms
  * Memory: 469852k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 const int N = 5e5 + ;

 typedef class TrieNode {
     public:
         int id;
         TrieNode* ch[];
         vector<int> vs;
 }TrieNode;

 TrieNode pool[N << ];
 TrieNode* top = pool;

 TrieNode* newnode() {
     top->id = ;
     top->ch[] = top->ch[] = NULL;
     return top++;
 }

 typedef class Trie {
     public:
         TrieNode* rt;

         Trie():rt(newnode()) {    }

         int insert(char* str, int id) {
             TrieNode* p = rt;
             for (int i = , c; str[i]; i++) {
                 c = str[i] - '';
                 if (!p->ch[c])
                     p->ch[c] = newnode();
                 p = p->ch[c];
             }
             if (!p->id)
                 p->id = id;
             else if ((!p->vs.size() || p->vs[p->vs.size() - ] != id - ) && p->id != id - )
                 p->vs.push_back(id);
             return p->id;
         }
 }Trie;

 int n, n2;
 char buf1[N], buf2[N];
 vector<int> g[N * ];
 // 1 ~ 2 * n2 : Is the node seclected?
 // 2 * n2 + 1 ~ 4 * n2: Aren't nodes above seclected?
 // 4 * n2 + 1 ~ 6 * n2: Aren't nodes below seclected?
 Trie tr;

 inline void init() {
     scanf("%d", &n);
     n2 = n << ;
     for (int i = , len, p1, p2; i <= n; i++) {
         scanf("%s", buf1);
         len = strlen(buf1);
         memcpy(buf2, buf1, len + );
         for (int j = ; j < len; j++)
             if (buf1[j] == '?')
                 buf1[j] = '';
         for (int j = ; j < len; j++)
             if (buf2[j] == '?')
                 buf2[j] = '';
         p1 = tr.insert(buf1, (i << ) - );
         p2 = tr.insert(buf2, i << );
         if (p1 == p2) {
             g[(i << ) -  + n2].push_back((i << ) - );
         } else {
             p1 = ((i << ) - ), p2 = (i << );
             g[p1].push_back(p2 + n2);
             g[p2 + n2].push_back(p1);
             g[p2].push_back(p1 + n2);
             g[p1 + n2].push_back(p2);
         }
     }
 }

 #define virt(_x) (_x + n2)
 #define upre(_x) (_x + n2 * 2)
 #define upvi(_x) (_x + n2 * 3)
 #define dore(_x) (_x + n2 * 4)
 #define dovi(_x) (_x + n2 * 5)

 void dfs(TrieNode* p, int last) {
     if (!p)    return;
     if (p->vs.size()) {
         vector<int> &ve = p->vs;
         for (int i = ; i < (signed) ve.size(); i++) {
             TrieNode* q = newnode();
             q->id = ve[i];
             q->ch[] = p->ch[], q->ch[] = p->ch[];
             p->ch[] = NULL, p->ch[] = q;
         }
         ve.clear();
     }
     int id = p->id;
     if (id) {
         g[id].push_back(upvi(id));
         g[id].push_back(dovi(id));
         g[upre(id)].push_back(virt(id));
         g[dore(id)].push_back(virt(id));
         if (last) {
             g[id].push_back(upre(last));
             g[upvi(last)].push_back(virt(id));
             g[last].push_back(dore(id));
             g[dovi(id)].push_back(virt(last));

             g[upre(id)].push_back(upre(last));
             g[upvi(last)].push_back(upvi(id));
             g[dore(last)].push_back(dore(id));
             g[dovi(id)].push_back(dovi(last));
         }
     }
     int nid = ((id) ? (id) : (last));
     dfs(p->ch[], nid);
     dfs(p->ch[], nid);
 }

 int dfs_clock = ;
 stack<int> st;
 boolean vis[N * ], ins[N * ];
 int dfn[N * ], low[N * ];
 void tarjan(int p) {
     vis[p] = true, ins[p] = true;
     dfn[p] = low[p] = ++dfs_clock;
     st.push(p);
     for (int i = ; i < (signed) g[p].size(); i++) {
         int e = g[p][i];
         if (!vis[e]) {
             tarjan(e);
             low[p] = min(low[p], low[e]);
         } else if (ins[e])
             low[p] = min(low[p], dfn[e]);
     }

     if (dfn[p] == low[p]) {
         int cur;
         do {
             cur = st.top();
             st.pop();
             low[cur] = low[p];
             ins[cur] = false;
         } while (cur != p);
     }
 }

 void putans(const char* str) {
     puts(str);
     exit();
 }

 inline void solve() {
     dfs(tr.rt, );
     for (int i = ; i <= n2 * ; i++)
         if (!vis[i])
             tarjan(i);
     for (int i = ; i <= n2; i++) {
         if (low[i] == low[virt(i)])
             putans("NO");
         if (low[upre(i)] == low[upvi(i)])
             putans("NO");
         if (low[dore(i)] == low[dovi(i)])
             putans("NO");
     }
     putans("YES");
 }

 int main() {
     init();
     solve();
     return ;
 }