MT【72】一个不等式
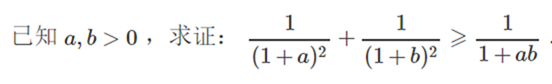
证明:

评: 可以思考$\frac{1}{(1+b)^2}+\frac{1}{(1+a)^2}$与$\frac{2}{(1+\sqrt{ab})^2}$大小。
MT【72】一个不等式的更多相关文章
- MT【10】和三次有关的一个因式分解
解答: 评:1此处因式分解也可以看成关于$a$的函数$f(a)$利用多项式有理根的有关知识得到 2.此处我们可以得到关于$\Delta ABC$的余弦的一个不等式$cosA+cosB+cosC> ...
- MT【146】一边柯西,一边舍弃
(2018浙江省赛9题)设$x,y\in R$满足$x-6\sqrt{y}-4\sqrt{x-y}+12=0$,求$x$的范围______ 解答:$x+12=6\sqrt{y}+4\sqrt{x-y} ...
- BZOJ2801/洛谷P3544 [POI2012]BEZ-Minimalist Security(题目性质发掘+图的遍历+解不等式组)
题面戳这 化下题面给的式子: \(z_u+z_v=p_u+p_v-b_{u,v}\) 发现\(p_u+p_v-b_{u,v}\)是确定的,所以只要确定了一个点\(i\)的权值\(x_i\),和它在同一 ...
- MT【207】|ax^2+bx+c|中判别式$\Delta$的含义
已知$a,b\in R^+,a+b=2$且对任意的$x\in R$,均有$|2x^2+ax-b|\ge|x^2+cx+d|$则$\dfrac{d-4c}{cd}$的最小值______ 提示:注意到$\ ...
- MT【190】绝对值的和
(2012浙江压轴题)已知$a>0,b\in R$,函数$f(x)=4ax^3-2bx-a+b$.1)证明:当$0\le x\le 1$时,i)函数$f(x)$的最大值为$|2a-b|+a;$i ...
- MT【75】考察高斯函数的一道高考压轴题
解答:答案1,3,4. 这里关于高斯函数$[x]$的一个不等式是需要知道的$x-1<[x]\le x$,具体的:
- 含有不等式约束的优化问题——KKT条件
优化问题: 其中, 定义:对于一个不等式约束,如果,那么称不等式约束是处起作用的约束. 定义:设满足,设为起作用不等式约束的下标集: 如果向量:是线性无关的,则称是一个正则点. 下面给出某个点是局部极 ...
- Hermite 矩阵的特征值不等式
将要学习 关于 Hermite 矩阵的特征值不等式. Weyl 定理 以及推论. Weyl 定理 Hermann Weyl 的如下定理是大量不等式的基础,这些不等式要么涉及两个 Hermite 矩 ...
- 【Luogu】 P5482 [JLOI2011]不等式组 题解
本来以为有多难,结果发现是道树状数组水题... 显然,对于每一个添加的不等式,有3种情况: \(a<0\) .此时可转换为 $x < {{a} \over {c-b}} $ . 但是,我们 ...
随机推荐
- odoo订餐系统之类型设计
这次开发的模块是订餐的类型设计,比如大荤 小荤 蔬菜 米饭 等基本数据.1.设计model类,很简单就一个字段: class MyLunchProductionCategory(osv.Model): ...
- Intel x86_64 Architecture Background 1
首先讲一下什么是Intel x86,x86是指intel的开发的一种32位指令集,从386开始时代开始的一直沿用至今,是一种cisc指令集.x84_64是x86 CPU开始迈向64位的时候,有2选择: ...
- Elasticsearch Query DSL 整理总结(四)—— Multi Match Query
目录 引言 概要 fields 字段 通配符 提升字段权重 multi_match查询的类型 best_fields 类型 dis_max 分离最大化查询 best_fields 维权使者 tie_b ...
- @Vue/Cli 3 关于 render 空的处理
问题场景 vue-cli 3 在打包部署时候会出现 dist folder not working "Uncaught TypeError: Cannot set property 'ren ...
- .NetCore实践篇:分布式监控系统zipkin踩坑之路(二)
前言 <牧神记>有一句话说的好,破心中神.当不再对分布式,微服务,CLR畏惧迷茫的时候,你就破了心中神. zipkin复习 第一篇: .Net架构篇:思考如何设计一款实用的分布式监控系统? ...
- 【下一代核心技术DevOps】:(二)Rancher的应用及优点简介
1.环境选择 安装Rancher环境,一定要在干净的linux主机上进行,避免出现因配置导致的莫名其妙的问题.服务器操作系统建议CentOS7.4(内核3.10以上)低于这个版本的系统 如7.3 7. ...
- 普通程序员看k8s基于角色的访问控制(RBAC)
一.知识准备 ● 上一节描述了k8s的账户管理,本文描述基于角色的访问控制 ● 网上RBAC的文章非常多,具体概念大神们也解释得很详细,本文没有站在高屋建瓴的角度去描述RBAC,而是站在一个普通程序员 ...
- python升级后带来的几个小问题
1)python升级带来的yum异常:File "/usr/bin/yum", line 30 原因:这是因为yum采用Python作为命令解释器,这可以从/usr/bin/yum ...
- LINUX第三次实践:程序破解
LINUX第三次实践:程序破解 标签(空格分隔): 20135328陈都 一.掌握NOP.JNE.JE.JMP.CMP汇编指令的机器码 NOP:NOP指令即"空指令".执行到NOP ...
- springboot整合fastJson遇到重定向问题
通过网上教程使用springboot整合fastJson后遇到页面重定向问题(使用的springboot版本是2.0.2.RELEASE ,其他的版本可能不会出现以下问题),如下图: 我的项目结构如下 ...
