Java-贪心算法

1. 什么是贪心算法？
　　贪心算法，又称贪婪算法(Greedy Algorithm)，是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优解出发来考虑，它所做出的仅是在某种意义上的局部最优解。
　　贪婪算法是一种分阶段的工作，在每一个阶段，可以认为所做决定是最好的，而不考虑将来的后果。这种“眼下能够拿到的就拿”的策略是这类算法名称的来源。
　　贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择。必须注意的是，贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。

二、贪心算法的基本思路：
1. 建立数学模型来描述问题。
2. 把求解的问题分成若干个子问题。
3. 对每一子问题求解，得到子问题的局部最优解。
4. 把子问题的解局部最优解合成原来解问题的一个解。

三、贪心算法适用的问题
　　贪心策略适用的前提是：局部最优策略能导致产生全局最优解。也就是当算法终止的时候，局部最优等于全局最优。

四、贪心算法的实现框架
从问题的某一初始解出发；
while （能朝给定总目标前进一步）
{
利用可行的决策，求出可行解的一个解元素；
}
由所有解元素组合成问题的一个可行解；

五、贪心策略的选择
　　因为用贪心算法只能通过解局部最优解的策略来达到全局最优解，因此，一定要注意判断问题是否适合采用贪心算法策略，找到的解是否一定是问题的最优解。
如果确定可以使用贪心算法，那一定要选择合适的贪心策略；

六、贪心算法的几个例子

1. 纸币找零问题

假设1元、2元、5元、10元、20元、50元、100元的纸币，张数不限制，现在要用来支付K元，至少要多少张纸币？

很显然，我们很容易就想到使用贪心算法来解决，并且我们所根据的贪心策略是，每一步尽可能用面值大的纸币即可。当然这是正确的，代码如下：

/**
     * 钱币找零问题
     *
     * @param money the money
     */
    public static void greedyGiveMoney(int money) {
        System.out.println("需要找零: " + money);
        int[] moneyLevel = {1, 5, 10, 20, 50, 100};
        for (int i = moneyLevel.length - 1; i >= 0; i--) {
            int num = money/ moneyLevel[i];
            int mod = money % moneyLevel[i];
            money = mod;
            if (num > 0) {
                System.out.println("需要" + num + "张" + moneyLevel[i] + "块的");
            }
        }
    }

（1）如果不限制纸币的金额，那这种情况还适合用贪心算法么。比如1元，2元，3元，4元，8元，15元的纸币，用来支付K元，至少多少张纸币？

经我们分析，这种情况是不适合用贪心算法的，因为我们上面提供的贪心策略不是最优解。比如，纸币1元，5元，6元，要支付10元的话，按照上面的算法，至少需要1张6元的，4张1元的，而实际上最优的应该是2张5元的。

（2）如果限制纸币的张数，那这种情况还适合用贪心算法么。比如1元10张，2元20张，5元1张，用来支付K元，至少多少张纸币？

同样，仔细想一下，就知道这种情况也是不适合用贪心算法的。比如1元10张，20元5张，50元1张，那用来支付60元，按照上面的算法，至少需要1张50元，10张1元，而实际上使用3张20元的即可；

（3）所以贪心算法是一种在某种范围内，局部最优的算法。

2. 背包问题： 
有一个背包，背包容量是W=150。有7个物品，每个物品有各自的重量和价值，每个物品有一件。要求尽可能让装入背包中的物品总价值最大，但不能超过总容量。
物品 A B C D E F G 
重量 35 30 60 50 40 10 25 
价值 10 40 30 50 35 40 30

我们很容易想到使用贪心算法来解决这个问题，那我们考虑一下贪心策略：

（1）每次挑选价值最大的物品放入背包，得到的结果是否最优？

（2）每次挑选所占重量最小的物品放入背包，得到的结果是否最优？

（3）每次选取单位重量价值最大的物品，得到的结果是否最优？

值得注意的是，贪心算法并不是完全不可以使用，贪心策略一旦经过证明成立后，它就是一种高效的算法。但可惜的是，它需要证明后才能真正运用到题目的算法中。

而上面的3中贪心策略，都是无法成立的，即无法被证明的：

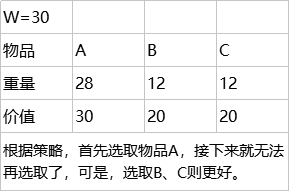
第一条和第二条类似，第三条，选取单位重量价值最大的物品：

以上问题使用贪心算法是解决不了的，而普通背包问题可以使用贪心算法来解决。这个问题是属于0-1背包问题，不过我们可以考虑使用动态规划来解决，那就是另一个问题了。

普通背包问题和0-1背包问题差不多，0-1背包的每件物品只有一件，而普通背包的每件物品数量是不止一件的，如果每件物品的数量是无限的，那这种称为完全背包问题；

参考自：http://blog.csdn.net/wang704987562/article/details/70991590

和《数据结构与算法分析 Java语音描述》